描述
在大学期间,经常需要租借教室。大到院系举办活动,小到学习小组自习讨论,都需要向学校申请借教室。教室的大小功能不同,借教室人的身份不同,借教室的手续也不一样。
面对海量租借教室的信息,LLQ自然希望编程解决这个问题。LLQ需要处理接下来n天的借教室信息,其中第i天学校有ri个教室可供租借。共有m份订单,每份订单用三个正整数描述,分别为dj,sj,tj,表示某租借者需要从第sj天到第tj天租借教室(包括第sj天和第tj天),每天需要租借dj个教室。
LLQ假定,租借者对教室的大小、地点没有要求。即对于每份订单,LLQ只需要每天提供dj个教室,而它们具体是哪些教室,每天是否是相同的教室则不用考虑。
借教室的原则是先到先得,也就是说LLQ要按照订单的先后顺序依次为每份订单分配教室。如果在分配的过程中遇到一份订单无法完全满足,则需要停止教室的分配,通知当前申请人修改订单。这里的无法满足指从第sj天到第tj天中有至少一天剩余的教室数量不足dj个。
现在LLQ需要知道,是否会有订单无法完全满足。如果有,需要通知哪一个申请人修改订单。
格式
输入格式
第一行包含两个正整数n,m,表示天数和订单的数量。
第二行包含n个正整数,其中第i个数为ri,表示第i天可用于租借的教室数量。
接下来有m行,每行包含三个正整数dj,sj,tj,表示租借的数量,租借开始、结束分别在第几天。
每行相邻的两个数之间均用一个空格隔开。天数与订单均用从1开始的整数编号。
输出格式
如果所有订单均可满足,则输出只有一行,包含一个整数0。否则(订单无法完全满足)输出两行,第一行输出一个负整数-1,第二行输出需要修改订单的申请人编号。
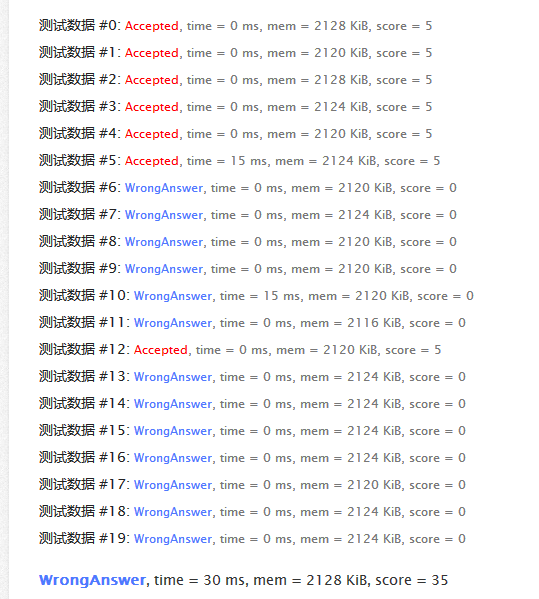
#include<cstdio>
#include<iostream>
#include<cstring>
#include<cstdlib>
using namespace std;
int m,n;
struct node{
int d,s,t;//数量,开始,结束
}k[100005];
int day[100005];
int main()
{
//ios::sync_with_stdio(false);
freopen("classroom.in","r",stdin);
freopen("classroom.out","w",stdout);
scanf("%d %d",&n,&m);//cin>>n>>m;
if(n>=100000)
{
cout<<0;
exit(0);
}
for(int i=1;i<=n;i++)
scanf("%d ",&day[i]);//cin>>day[i];
for(int i=1;i<=m;i++)
{
int x,y,z;
scanf("%d %d %d",&x,&y,&z);//cin>>x>>y>>z;
// k[i].d=x,k[i].s=y,k[i].t=z;
for(int j=y;j<=z;j++)
{
day[j]-=x;
if(day[j]<0)
{
cout<<-1<<endl;
cout<<i;
exit(0);
}
}
}
cout<<0;
return 0;
}
呵呵。。。。
二、线段树:
刚看到题肯定立马会想到这种解法,太经典了。
就是代码稍稍长了那么一丢丢。
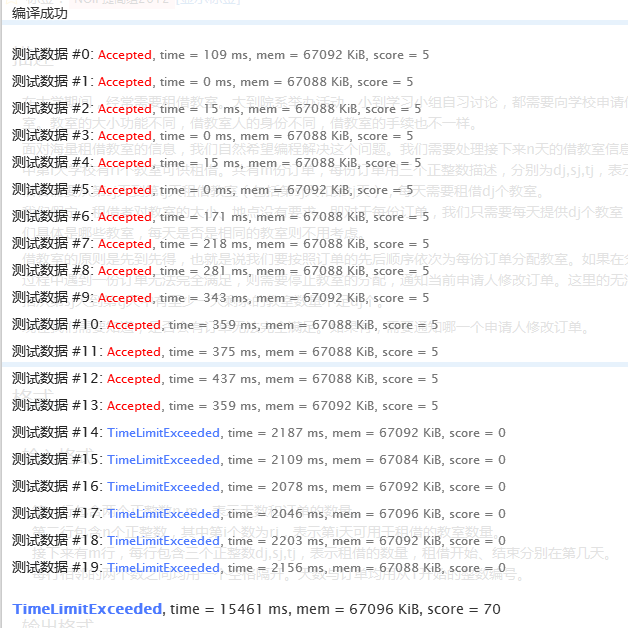
代码:
#include<cstdio>
#include<iostream>
#include<cstring>
#include<cmath>
#include<cstdlib>
#define L(u) (u*2)
#define R(u) (u*2+1)
#define MAXN 1000005
int m,n;
int a[MAXN];int w;
using namespace std;
struct node{
int minl,x,l,r;//x:减量
}s[4*MAXN];
void pushdown(int u)
{
s[L(u)].x+=s[u].x;
s[L(u)].minl-=s[u].x;
s[R(u)].x+=s[u].x;
s[R(u)].minl-=s[u].x;
s[u].x=0;
}
void pushup(int u)
{
s[u].minl=min(s[L(u)].minl,s[R(u)].minl);
return ;
}
void buildtree(int u,int left,int right)
{
s[u].l=left,s[u].r=right;
if(left==right)
{
s[u].minl=a[left];
return ;
}
int mid=(left+right)>>1;
buildtree(L(u),left,mid);
buildtree(R(u),mid+1,right);
pushup(u);
}
void update(int u,int left,int right)
{
if(s[u].l==left&&s[u].r==right)
{
pushdown(u);
s[u].x+=w;//减量
s[u].minl-=s[u].x;
return;
}
if (s[u].x)pushdown(u);
int mid=(s[u].l+s[u].r)>>1;
if(left>mid)
update(R(u),left,right);
else if(right<=mid)
update(L(u),left,right);
else
{
update(L(u),left,mid);
update(R(u),mid+1,right);
}
pushup(u);
}
int main()
{
ios::sync_with_stdio(false);
freopen("classroom.in","r",stdin);
freopen("classroom.out","w",stdout);
cin>>n>>m;
for(int i=1;i<=n;i++)
cin>>a[i];
buildtree(1,1,n);
for(int i=1;i<=m;i++)
{
int x,y;
cin>>w>>x>>y;
update(1,x,y);
if(s[1].minl<0)
{
cout<<-1<<endl;
cout<<i;
exit(0);
}
}
cout<<0;
return 0;
}
这种方法思路很清晰,很好写。
三、二分求解:
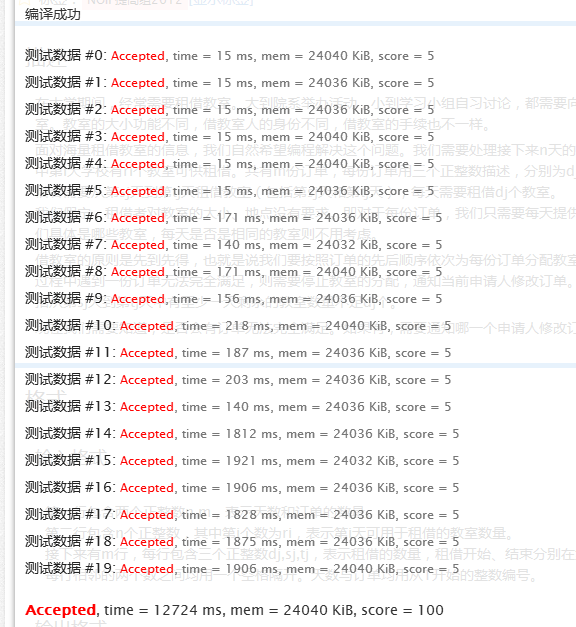
一种神奇的算法。。祥解见代码中:
#include<cstdio>
#include<cstring>
#include<iostream>
using namespace std;
int r[1000005];
int d[1000005],s[1000005],t[1000005];
int a[1000005],sum[1000005];
int n,m;
bool pd(int mid)
{
memset(a,0,sizeof(a));
memset(sum,0,sizeof(sum));
for(int i=1;i<=mid;i++)
{
a[s[i]]+=d[i];//起点加上,终点的下一个点减去,画了图后就会发现这个方法十分的神奇~
a[t[i]+1]-=d[i];
}
for(int i=1;i<=n;i++)
{
sum[i]=sum[i-1]+a[i];//判断是否超过限制
if(sum[i]>r[i])return false; //超过输入数据
}
return true;//若不存在上面的情况则说明可以借
}
int main()
{
//ios::sync_with_stdio(false);
freopen("classroom.in","r",stdin);
freopen("classroom.out","w",stdout);
scanf("%d%d",&n,&m);//cin>>n>>m;
for(int i=1;i<=n;i++)
scanf("%d",&r[i]);//cin>>r[i];
for(int i=1;i<=m;i++)
scanf("%d %d %d",&d[i],&s[i],&t[i]);//数量,起始,终点
int l=1,r=m;
while(l+1<r)
{
int mid=(l+r)>>1;
if(pd(mid))//二分查找
l=mid;
else
r=mid;
}
bool t1=pd(l),t2=pd(r);//t2=pd(r);
if(!t1)//左端点
{
printf("-1
%d",l);
//cout<<-1<<endl;
//cout<<l;
}
else if(!t2)//右端点
{
printf("-1
%d",r);
//cout<<-1<<endl;
//cout<<r;
}
else printf("0");//cout<<0;若都不是,则不存在修改,输出0
return 0;
}
二分最烦的就是断点取值和mid的赋值了,很容易错。这里我用的是二分到区间长度为1再判断。
完美AC~~~~~~~~~