L3-012 水果忍者 （30 分）

2010年风靡全球的“水果忍者”游戏，想必大家肯定都玩过吧？（没玩过也没关系啦~）在游戏当中，画面里会随机地弹射出一系列的水果与炸弹，玩家尽可能砍掉所有的水果而避免砍中炸弹，就可以完成游戏规定的任务。如果玩家可以一刀砍下画面当中一连串的水果，则会有额外的奖励，如图1所示。

图 1

现在假如你是“水果忍者”游戏的玩家，你要做的一件事情就是，将画面当中的水果一刀砍下。这个问题看上去有些复杂，让我们把问题简化一些。我们将游戏世界想象成一个二维的平面。游戏当中的每个水果被简化成一条一条的垂直于水平线的竖直线段。而一刀砍下我们也仅考虑成能否找到一条直线，使之可以穿过所有代表水果的线段。

图 2

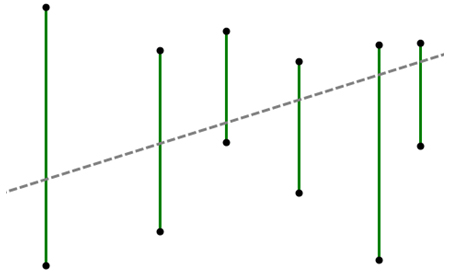
如图2所示，其中绿色的垂直线段表示的就是一个一个的水果；灰色的虚线即表示穿过所有线段的某一条直线。可以从上图当中看出，对于这样一组线段的排列，我们是可以找到一刀切开所有水果的方案的。

另外，我们约定，如果某条直线恰好穿过了线段的端点也表示它砍中了这个线段所表示的水果。假如你是这样一个功能的开发者，你要如何来找到一条穿过它们的直线呢？

输入格式：

输入在第一行给出一个正整数N（≤），表示水果的个数。随后N行，每行给出三个整数x、y​1​​、y​2​​，其间以空格分隔，表示一条端点为(和(的水果，其中y​1​​>y​2​​。注意：给出的水果输入集合一定存在一条可以将其全部穿过的直线，不需考虑不存在的情况。坐标为区间 [ 内的整数。

输出格式：

在一行中输出穿过所有线段的直线上具有整数坐标的任意两点(和(，格式为 y​1​​。注意：本题答案不唯一，由特殊裁判程序判定，但一定存在四个坐标全是整数的解。

输入样例：

5
-30 -52 -84
38 22 -49
-99 -22 -99
48 59 -18
-36 -50 -72

输出样例：

-99 -99 -30 -52
题意：给出一些平行于y轴的线段，要求找到一条直线可以穿过（经过端点也可）所有线段，输出直线上的两个点，要求都是整数。
注意：如果只有一条线段，自己本身就是答案，可能存在多条直线重合，只需要记录y最小的上端点和y最大的下端点。
方法：根据求凸包的原理，分别用栈辅助去除使得上端点连线上凸的点以及使得下端点连线下凹的点，存下剩下的点，可以连成两条折线，那么满足条件的直线就在两线之间，枚举折线的每个线段，找到满足条件的。
输入样例可以得到如下图：

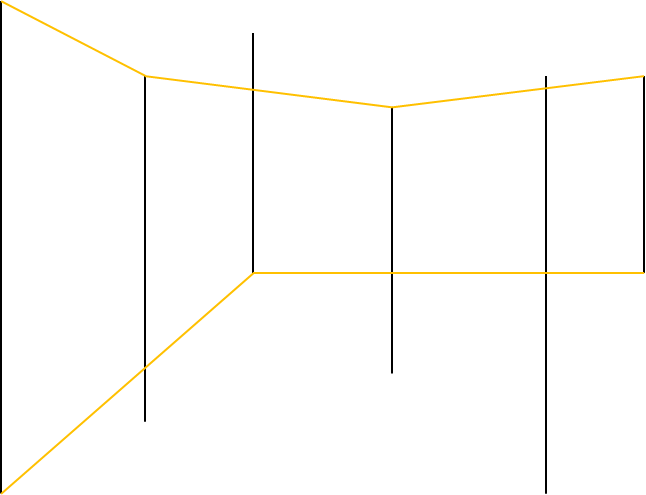
黄色线是栈里保存的点连成的折线。

代码：

#include <iostream>
#include <cstdio>
#include <map>
#include <cstring>
#include <vector>
#include <algorithm>
#define inf 0x3f3f3f3f
using namespace std;

typedef long long ll;
typedef pair<int,int> pa;
int n;
vector<int> p;
pa u[10000],d[10000];
int uc,dc;
map<int,int> vis,up,down;
int lx,ly,rx,ry;
inline bool pupl(const pa &p1,const pa &p2,const pa &p3) {
    return (ll)(p3.first - p2.first) * (p2.second - p1.second) > (ll)(p2.first - p1.first) * (p3.second - p2.second);
}
inline bool pdownl(const pa &p1,const pa &p2,const pa &p3) {
    return (ll)(p3.first - p2.first) * (p2.second - p1.second) < (ll)(p2.first - p1.first) * (p3.second - p2.second);
}
int main() {
    int x,y1,y2;
    scanf("%d",&n);
    for(int i = 0;i < n;i ++) {
        scanf("%d%d%d",&x,&y1,&y2);
        if(vis[x] == 0) {
            p.push_back(x);
            vis[x] = 1;
            up[x] = y1;
            down[x] = y2;
        }
        else {
            up[x] = min(up[x],y1);
            down[x] = min(down[x],y2);
        }
    }
    if(p.size() == 1) {
        lx = p[0];
        ly = up[p[0]];
        rx = p[0];
        ry = down[p[0]];
    }
    else {
        sort(p.begin(),p.end());
        for(int i = 0;i < p.size();i ++) {
            while(uc >= 2 && pupl(u[uc - 2],u[uc - 1],pa(p[i],up[p[i]]))) uc --;
            u[uc ++] = pa(p[i],up[p[i]]);
            while(dc >= 2 && pdownl(d[dc - 2],d[dc - 1],pa(p[i],down[p[i]]))) dc --;
            d[dc ++] = pa(p[i],down[p[i]]);
        }
        int i,j;
        for(i = 0;i < uc - 1;i ++) {
            for(j = 0;j < dc;j ++) {
                if(pupl(u[i],d[j],u[i + 1])) break;
            }
            if(j == dc) break;
        }
        if(i == uc - 1) {
            for(i = 0;i < dc - 1;i ++) {
                for(j = 0;j < uc;j ++) {
                    if(pdownl(d[i],u[j],d[i + 1])) break;
                }
                if(j == uc) break;
            }
            lx = d[i].first;
            ly = d[i].second;
            rx = d[i + 1].first;
            ry = d[i + 1].second;
        }
        else {
            lx = u[i].first;
            ly = u[i].second;
            rx = u[i + 1].first;
            ry = u[i + 1].second;
        }
    }
    printf("%d %d %d %d",lx,ly,rx,ry);
}