java-直接选择排序

直接选择排序是一种简单的排序方法，它每次从当前待排序的区间中选择出最小的元素，把该元素与该区间的第一个元素交换。

第一次从a[0]~a[n-1]中选取最小值，与a0]交换，第二次从a[1]~a[n-1]中选取最小值，与a[1]交换，....，第i次从a[i-1]~a[n-1]中选取最小值，与a[i-1]交换，.....，第n-1次从a[n-2]~a[n-1]中选取最小值，与a[n-2]交换，总共通过n-1次，得到一个按排序码从小到大排列的有序序列。

例如：假定n = 8，数组a中8个元素的排序码为：

　　　　(36,25,48,12,65,43,20,58)

如图给出了进行每次选择并交换后各排序码位置的变动情况，中括号中为待排序区间，中括号前面为已经排好的元素。

       

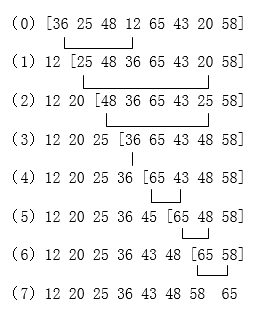
直接选择排序的算法用java描述为:

public static void selectionSort(int[] a,int n) {
        if(n>a.length) {
            System.out.println("超出数组长度");
            System.exit(1);
        }
        for (int i = 1; i < n; i++) {    //i表示次数，共进行n-1次选择和交换
            int minIndex = i-1;            //用minIndex表示最小元素的下标
            for (int j = i; j < n; j++) {//找到当前排序区间中最小元素的下标
                if(a[minIndex]>a[j]) {//如果后面的元素小于当前最小元素，则用minIndex记录下后面最小元素的下标
                    minIndex = j;
                }
            }
            if(minIndex != i) {//如果minIndex==i,说明minIndex就是当前排序区间首位元素的下标，因此不用交换
                int temp = a[i];
                a[i] = a[minIndex];
                a[minIndex] = temp;
            }
        }
    }

完整代码并测试：

import java.util.Scanner;

public class SelectionSort {
    public static void selectionSort(int[] a,int n) {
        if(n>a.length) {
            System.out.println("超出数组长度");
            System.exit(1);
        }
        for (int i = 1; i < n; i++) {    //i表示次数，共进行n-1次选择和交换
            int minIndex = i-1;            //用minIndex表示最小元素的下标
            for (int j = i; j < n; j++) {//找到当前排序区间中最小元素的下标
                if(a[minIndex]>a[j]) {//如果后面的元素小于当前最小元素，则用minIndex记录下后面最小元素的下标
                    minIndex = j;
                }
            }
            if(minIndex != i-1) {//如果minIndex==i-1,说明minIndex就是当前排序区间首位元素的下标，因此不用交换
                int temp = a[i-1];
                a[i-1] = a[minIndex];
                a[minIndex] = temp;
            }
        }
    }
    
    public static void main(String[] args) {
        Scanner input = new Scanner(System.in);
        System.out.println("请输入元素的个数");
        int n = input.nextInt();
        int[] a = new int[n];
        System.out.println("请依次输入元素");
        for (int i = 0; i < a.length; i++) {
            a[i] = input.nextInt();
        }
        System.out.println("请输入待排元素的个数");
        int m = input.nextInt();
        selectionSort(a,m);
        System.out.println("排序之后");
        for (int i = 0; i < a.length; i++) {
            System.out.print(a[i]+" ");
        }
    }
}

请输入元素的个数
8
请依次输入元素
36 25 48 12 65 43 20 58
请输入待排元素的个数
8
排序之后
12 20 25 36 43 48 58 65

效率：

在直接选择排序中，共需要进行n-1次选择和交换，每次选择需要比较n-i 次(1<=i<=n-1),每次交换最多需要3次移动，因此，总的比较次数：C=(n*n - n)/2,

总的移动次数(最大值)： 3(n-1).由此可知，直接选择排序的时间复杂度为 O(n^2)。由于在直接选择排序中存在着前后元素之间的互换，因而可能会改变相同元素的前后位置，如4,3,4,2 第一次4和2交换，第一个4跑到了第3个4之后，所以此方法是不稳定的。