数据结构百科定义
万维百科
在计算机科学中,数据结构(英语:data structure)是计算机中存储、组织数据的方式。
数据结构意味着接口或封装:一个数据结构可被视为两个函数之间的接口,或者是由数据类型联合组成的存储内容的访问方法封装。
大多数数据结构都由数列、记录、可辨识联合、引用等基本类型构成。举例而言,可为空的引用(nullable reference)是引用与可辨识联合的结合体,而最简单的链式结构链表则是由记录与可空引用构成。
数据结构可透过编程语言所提供的数据类型、引用及其他操作加以实现。一个设计良好的数据结构,应该在尽可能使用较少的时间与空间资源的前提下,支持各种程序运行。
不同种类的数据结构适合不同种类的应用,部分数据结构甚至是为了解决特定问题而设计出来的。例如B树即为加快树状结构访问速度而设计的数据结构,常被应用在数据库和文件系统上。
正确的数据结构选择可以提高算法的效率(请参考算法效率(英语:algorithmic efficiency))。在计算机程序设计的过程中,选择适当的数据结构是一项重要工作。许多大型系统的编写经验显示,程序设计的困难程度与最终成果的质量与表现,取决于是否选择了最适合的数据结构。
系统架构的关键因素是数据结构而非算法的见解,导致了多种形式化的设计方法与编程语言的出现。绝大多数的语言都带有某种程度上的模块化思想,透过将数据结构的具体实现封装隐藏于用户界面之后的方法,来让不同的应用程序能够安全地重用这些数据结构。C++、Java、Python等面向对象的编程语言可使用类 (计算机科学)来达到这个目的。
因为数据结构概念的普及,现代编程语言及其API中都包含了多种默认的数据结构,例如 C++ 标准模板库中的容器、Java集合框架以及微软的.NET Framework。
头条百科=百度百科
数据结构(data structure)是带有结构特性的数据元素的集合,它研究的是数据的逻辑结构和数据的物理结构以及它们之间的相互关系,并对这种结构定义相适应的运算,设计出相应的算法,并确保经过这些运算以后所得到的新结构仍保持原来的结构类型。简而言之,数据结构是相互之间存在一种或多种特定关系的数据元素的集合,即带“结构”的数据元素的集合。“结构”就是指数据元素之间存在的关系,分为逻辑结构和存储结构。
数据的逻辑结构和物理结构是数据结构的两个密切相关的方面,同一逻辑结构可以对应不同的存储结构。算法的设计取决于数据的逻辑结构,而算法的实现依赖于指定的存储结构。
数据结构的研究内容是构造复杂软件系统的基础,它的核心技术是分解与抽象。通过分解可以划分出数据的3个层次;再通过抽象,舍弃数据元素的具体内容,就得到逻辑结构。类似地,通过分解将处理要求划分成各种功能,再通过抽象舍弃实现细节,就得到运算的定义。上述两个方面的结合可以将问题变换为数据结构。这是一个从具体(即具体问题)到抽象(即数据结构)的过程。然后,通过增加对实现细节的考虑进一步得到存储结构和实现运算,从而完成设计任务。这是一个从抽象(即数据结构)到具体(即具体实现)的过程。
搜狗百科
数据结构是抽象数据类型的基础。不同类型的数据结构适用于不同类型的应用程序,有些数据结构高度专用于特定的任务。例如,关系数据库通常使用 B-树索引进行数据检索,而编译器实现通常使用哈希表来查找标识符。
数据结构为诸如大型数据库和互联网索引服务等用途提供了有效管理大量数据的手段。通常,高效的数据结构是设计高效的算法的关键。一些正式的设计方法和编程语言强调数据结构(而不是算法)作为软件设计中的关键组织因素。数据结构可用于组织存储在主存储器和辅助存储器中的信息的存储和检索。
集合,列表与数组
集合
集合一般被定义为:由一个或多个确定的元素所构成的整体。
集合有什么特性呢?
首先,集合里的元素类型不一定相同。 你可以将商品看作一个集合,也可以将整个商店看作一个集合,这个商店中有人或者其他物品也没有关系。
其次,集合里的元素没有顺序。 我们不会这样讲:我想要集合中的第三个元素,因为集合是没有顺序的。
事实上,这样的集合并不直接存在于编程语言中。然而,实际编程语言中的很多数据结构,就是在集合的基础上添加了一些规则形成的。
列表
列表(又称线性列表)的定义为:是一种数据项构成的有限序列,即按照一定的线性顺序,排列而成的数据项的集合。
列表的概念是在集合的特征上形成的,它具有顺序,且长度是可变的。你可以把它看作一张购物清单:

在这张清单中:
购物清单中的条目代表的类型可能不同,但是按照一定顺序进行了排列;
购物清单的长度是可变的,你可以向购物清单中增加、删除条目。
在编程语言中,列表最常见的表现形式有数组和链表,而我们熟悉的栈和队列则是两种特殊类型的列表。除此之外,向列表中添加、删除元素的具体实现方式会根据编程语言的不同而有所区分。
数组
数组是列表的实现方式之一,也是面试中经常涉及到的数据结构。
正如前面提到的,数组是列表的实现方式,它具有列表的特征,同时也具有自己的一些特征。然而,在具体的编程语言中,数组这个数据结构的实现方式具有一定差别。比如 C++ 和 Java 中,数组中的元素类型必须保持一致,而 Python 中则可以不同。Python 中的数组叫做 list,具有更多的高级功能。
那么如何从宏观上区分列表和数组呢?这里有一个重要的概念:索引。
首先,数组会用一些名为 索引 的数字来标识每项数据在数组中的位置,且在大多数编程语言中,索引是从 0 算起的。我们可以根据数组中的索引,快速访问数组中的元素。
而列表中没有索引,这是数组与列表最大的不同点。
其次,数组中的元素在内存中是连续存储的,且每个元素占用相同大小的内存。要理解这一点,我们需要了解数组在内存中的存储方式
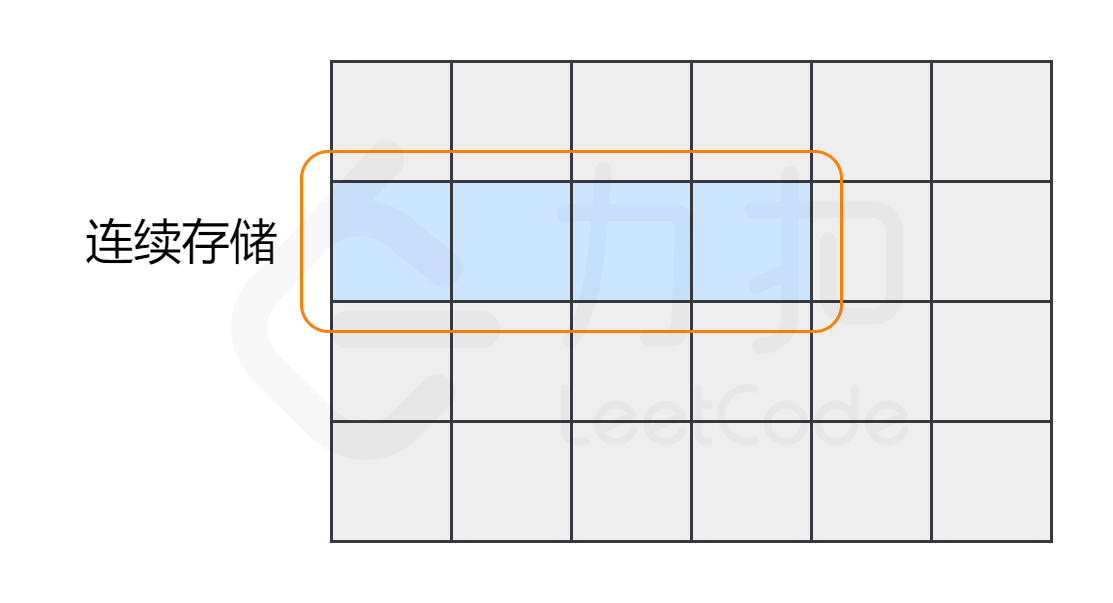
相反,列表中的元素在内存中可能彼此相邻,也可能不相邻。比如列表的另一种实现方式——链表,它的元素在内存中则不一定是连续的。
数组操作
读取元素
读取数组中的元素,是通过访问索引的方式来读取的,索引一般从 0 开始。
在计算机中,内存可以看成一些已经排列好的格子,每个格子对应一个内存地址。一般情况下,数据会分散地存储在不同的格子中。
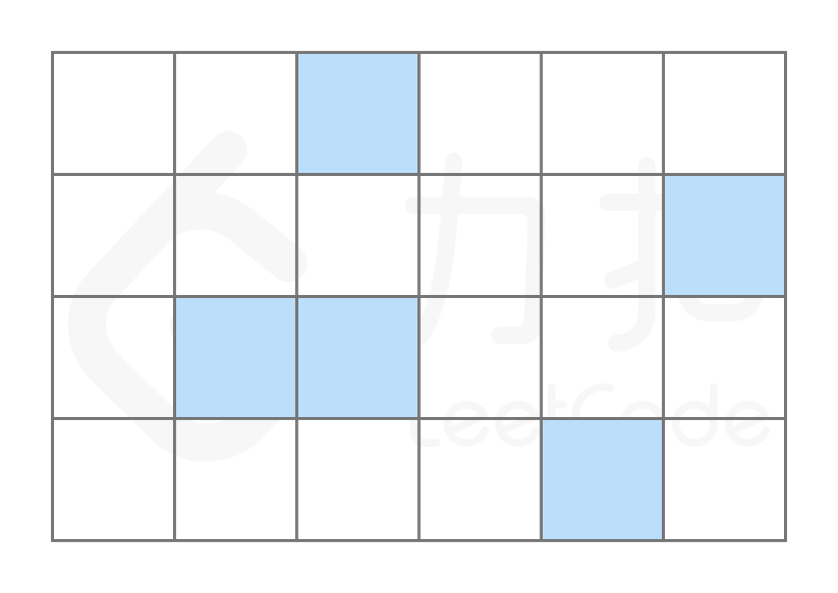
而对于数组,计算机会在内存中为其申请一段 连续 的空间,并且会记下索引为 0 处的内存地址。以数组 ["C", "O", "D", "E", "R"] 为例,它的各元素对应的索引及内存地址如下图所示。
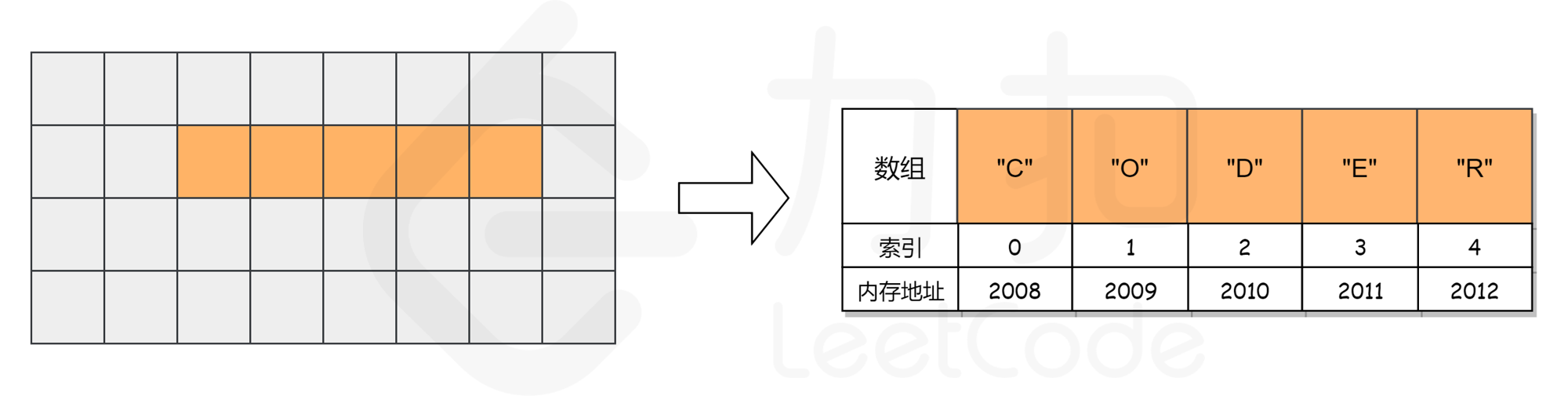
假如我们想要访问索引为 2 处的元素 "D" 时,计算机会进行以下计算:
找到该数组的索引 0 的内存地址: 2008;
将内存地址加上索引值,作为目标元素的地址,即 2008 + 2 = 2010,对应的元素为 "D",这时便找到了目标元素。
我们知道,计算内存地址这个过程是很快的,而我们一旦知道了内存地址就可以立即访问到该元素,因此它的时间复杂度是常数级别,为 O(1)O(1)O(1)。
查找元素
假如我们对数组中包含哪些元素并不了解,只是想知道其中是否含有元素 "E",数组会如何查找元素 `"E" 呢?
与读取元素类似,由于我们只保存了索引为 0 处的内存地址,因此在查找元素时,只需从数组开头逐步向后查找就可以了。如果数组中的某个元素为目标元素,则停止查找;否则继续搜索直到到达数组的末尾。
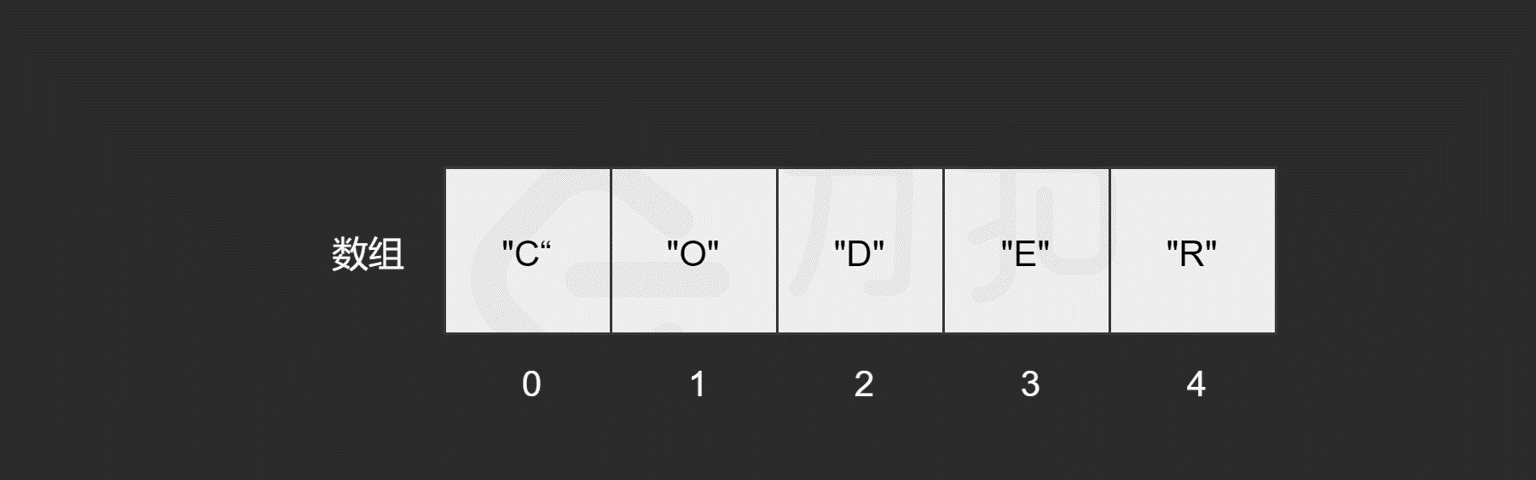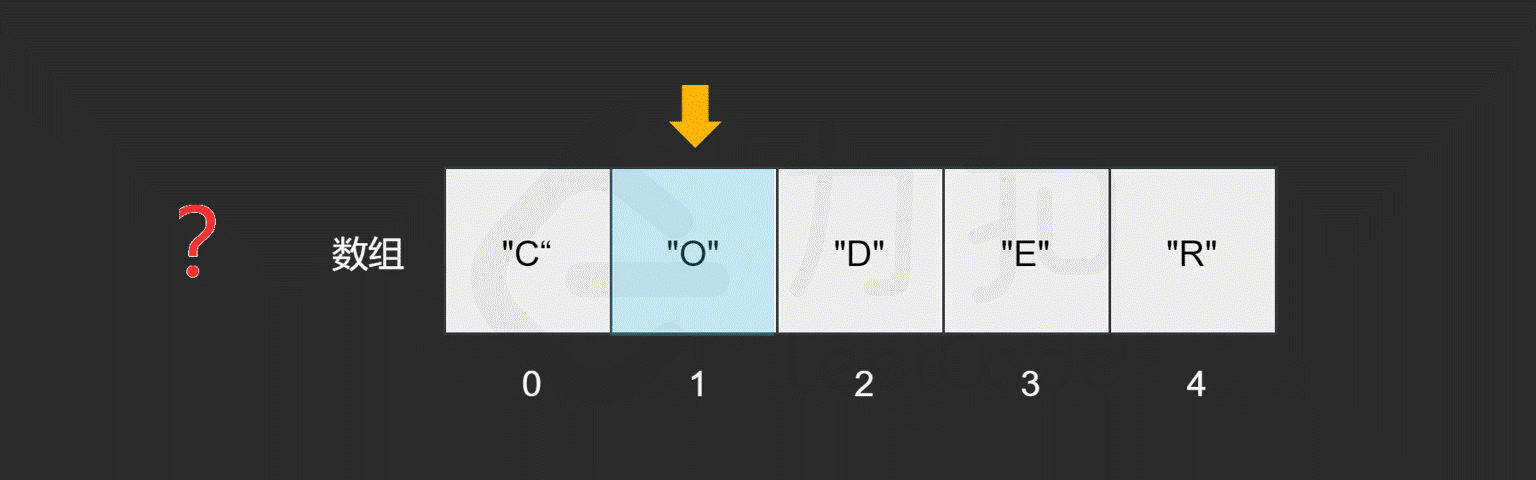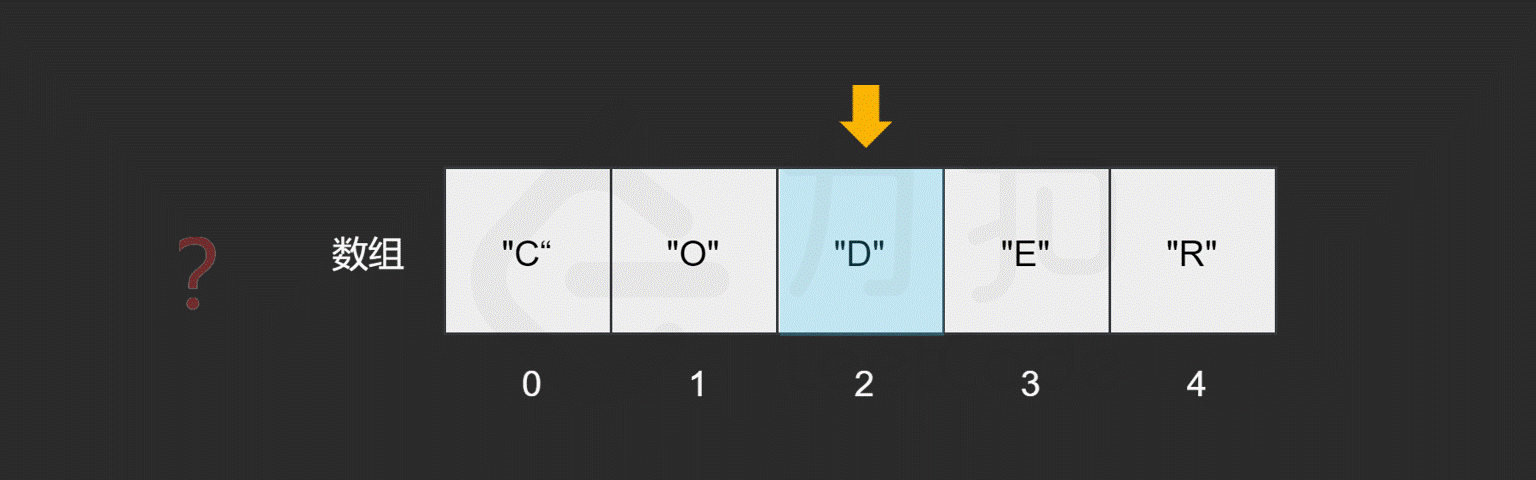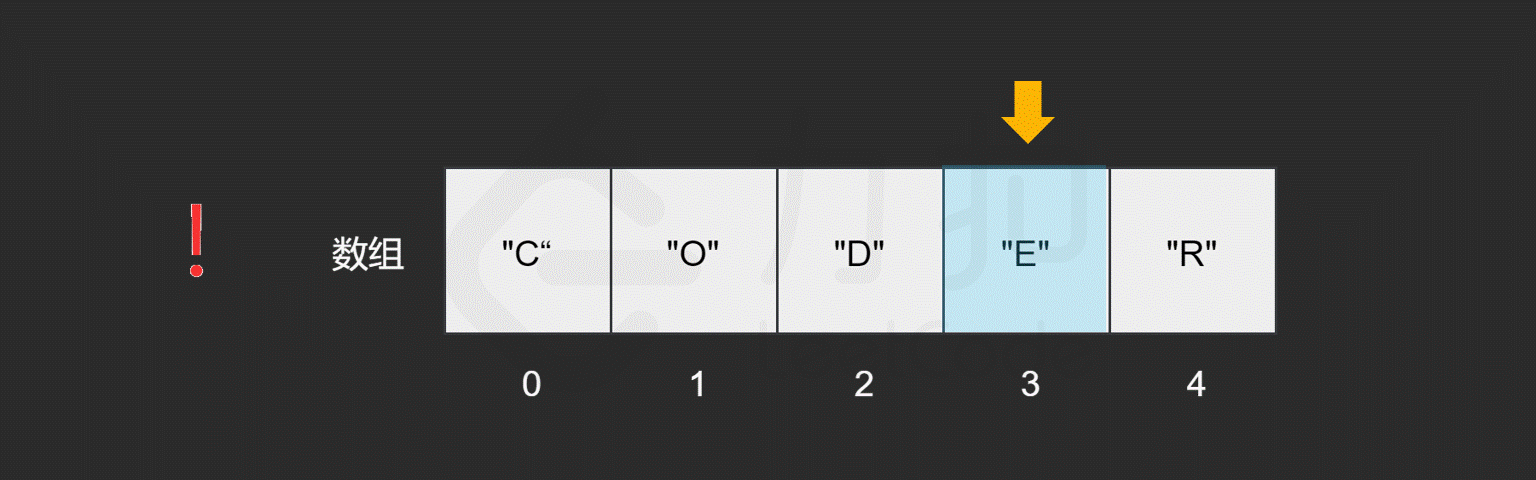
我们发现,最坏情况下,搜索的元素为 "R",或者数组中不包含目标元素时,我们需要查找 n 次,n 为数组的长度,因此查找元素的时间复杂度为 O(N)O(N)O(N),NNN。
插入元素
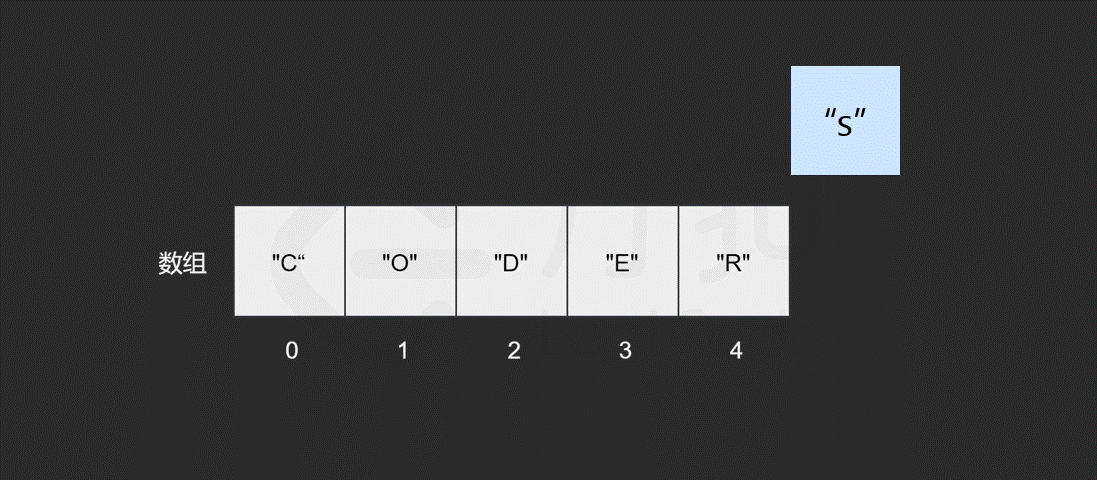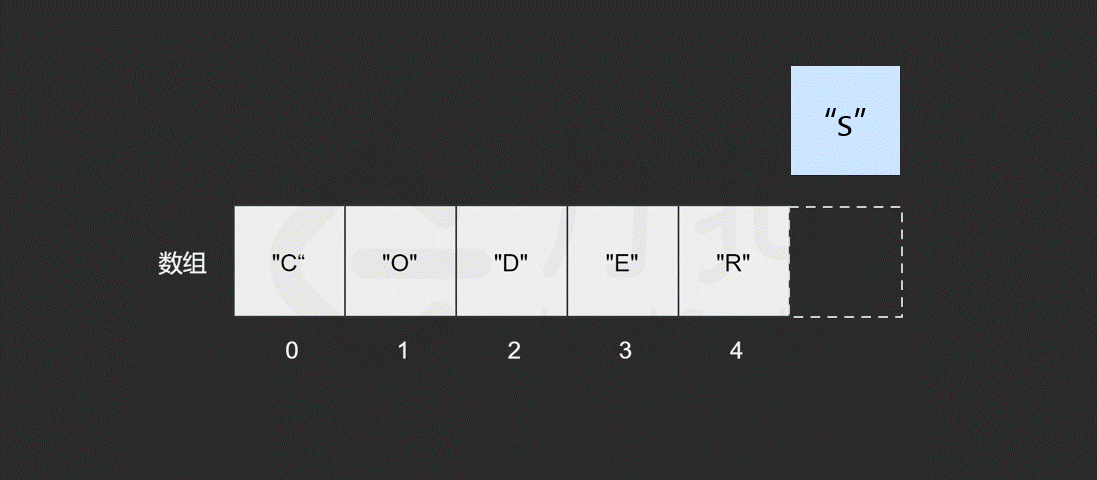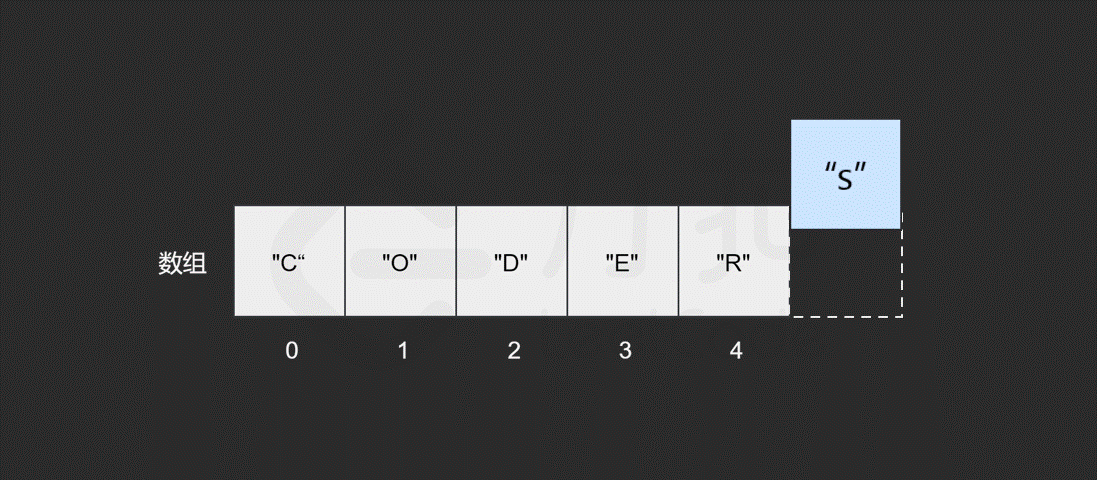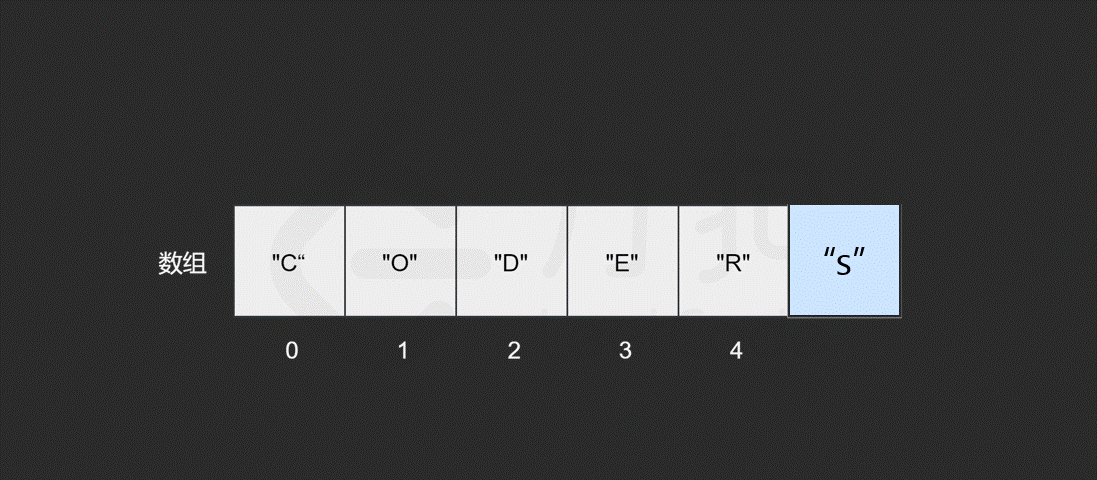
假如我们想在原有的数组中再插入一个元素 "S" 呢?
如果要将该元素插入到数组的末尾,只需要一步。即计算机通过数组的长度和位置计算出即将插入元素的内存地址,然后将该元素插入到指定位置即可。
然而,如果要将该元素插入到数组中的其他位置,则会有所区别,这时我们首先需要为该元素所要插入的位置 腾出 空间,然后进行插入操作。比如,我们想要在索引 2 处插入 "S"。
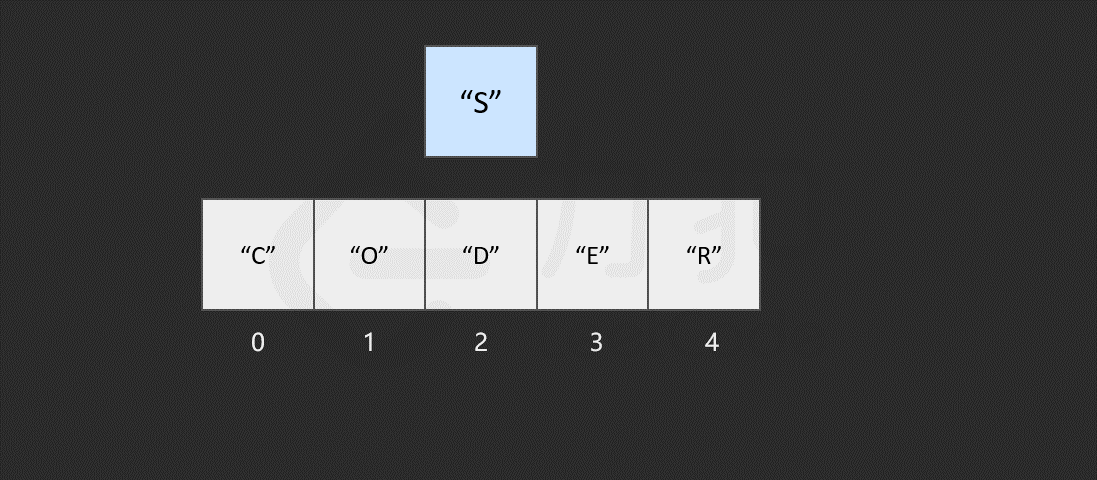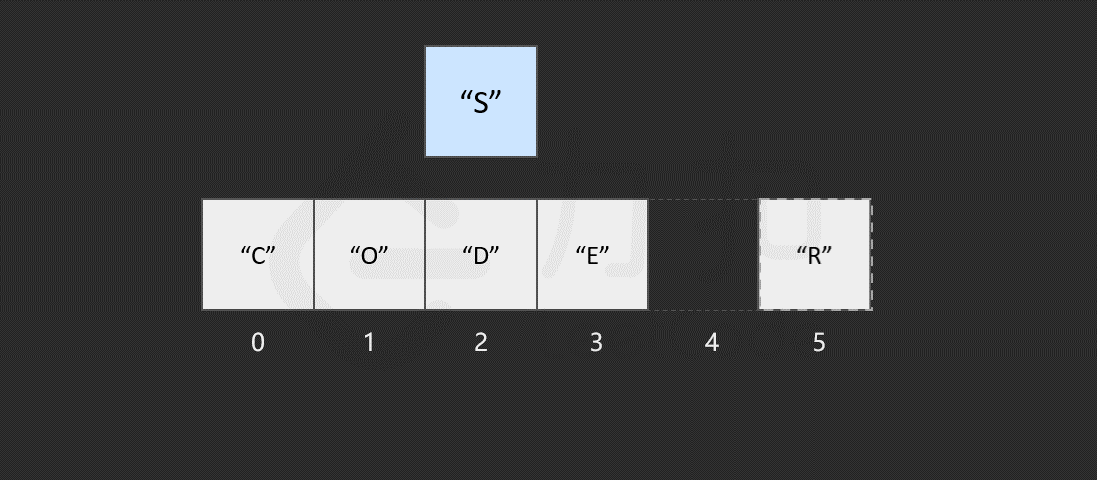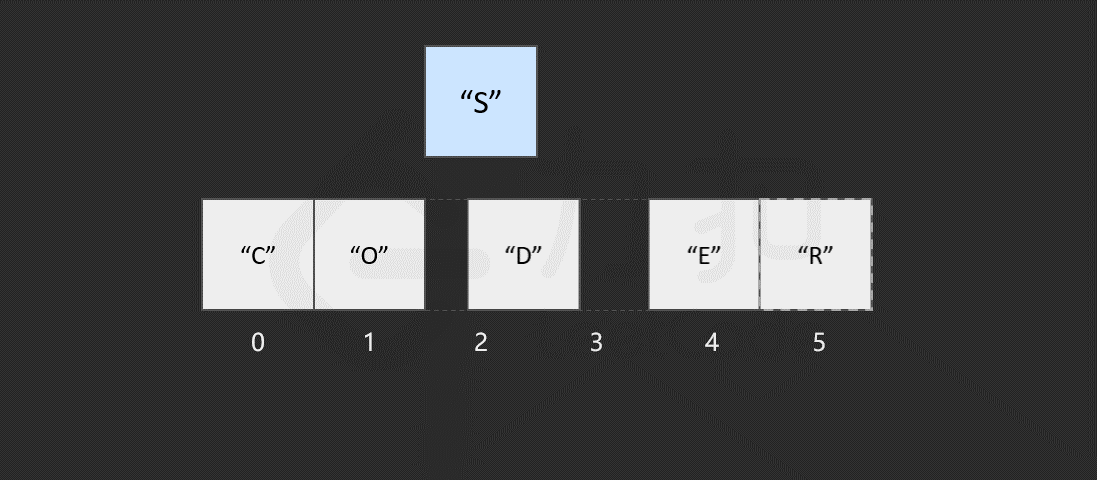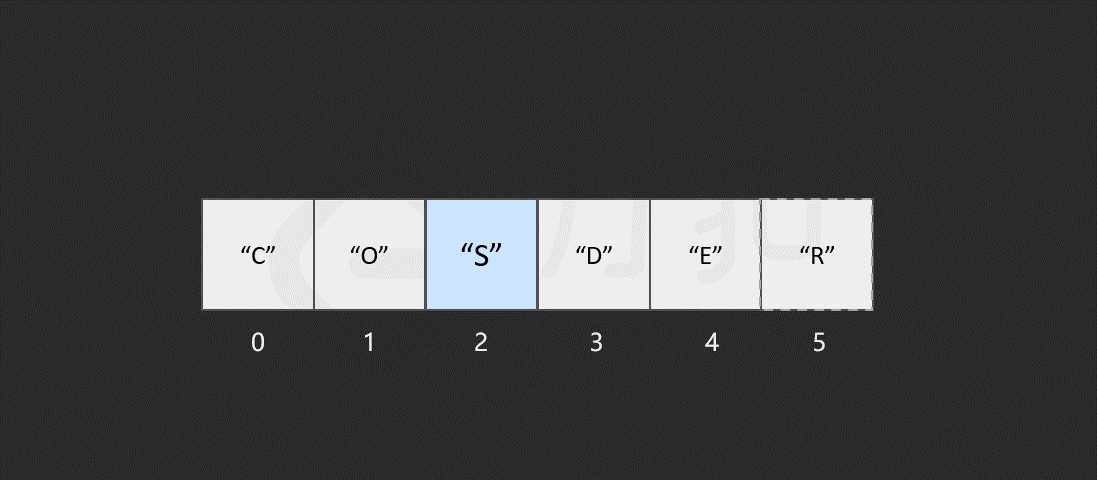
我们发现,如果需要频繁地对数组元素进行插入操作,会造成时间的浪费。事实上,另一种数据结构,即链表可以有效解决这个问题
删除元素
删除元素与插入元素的操作类似,当我们删除掉数组中的某个元素后,数组中会留下 空缺 的位置,而数组中的元素在内存中是连续的,这就使得后面的元素需对该位置进行 填补 操作。
以删除索引 1 中的元素 "O" 为例,具体过程如图所示。
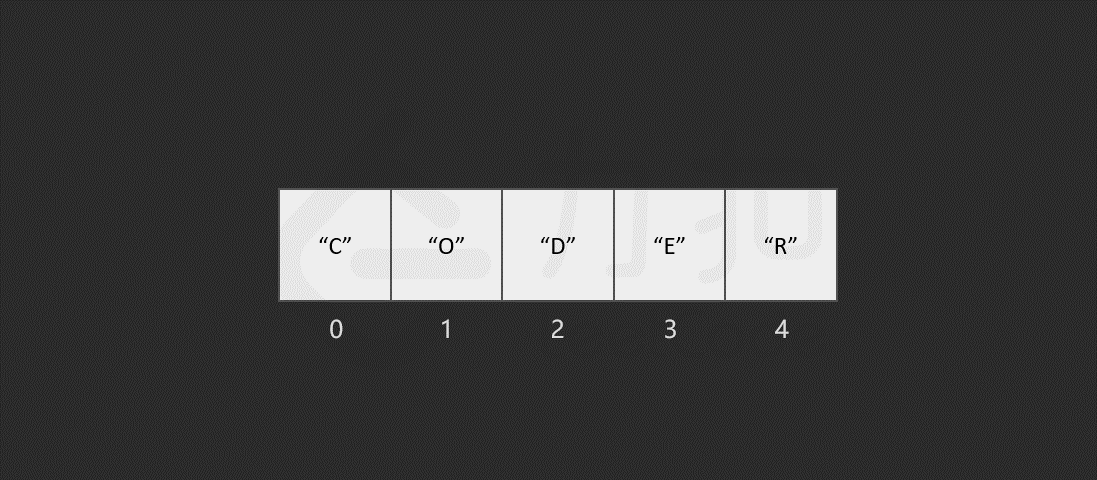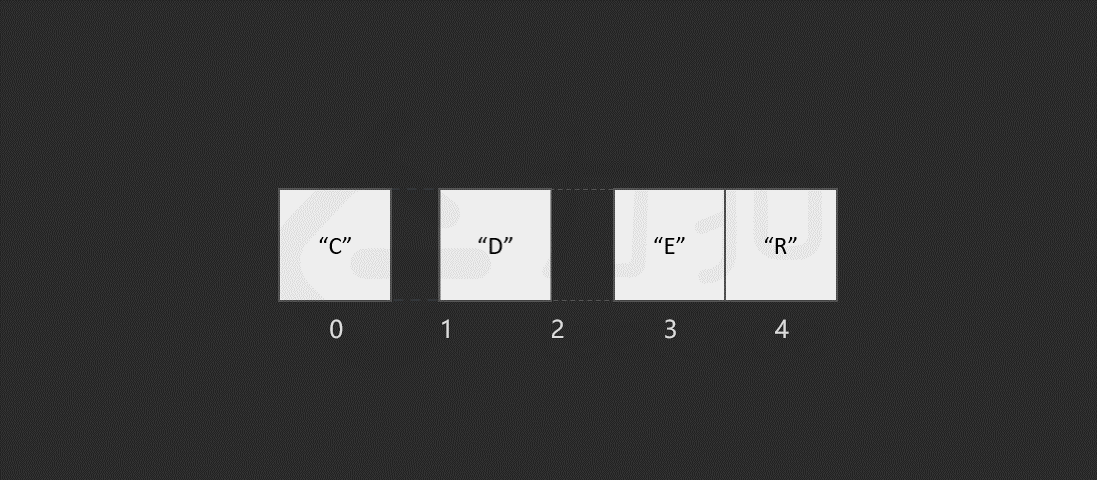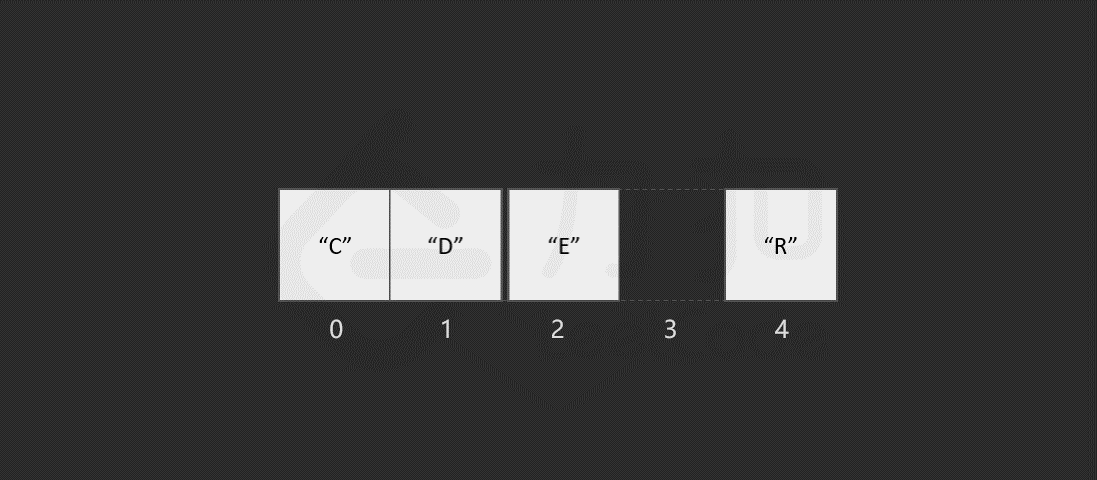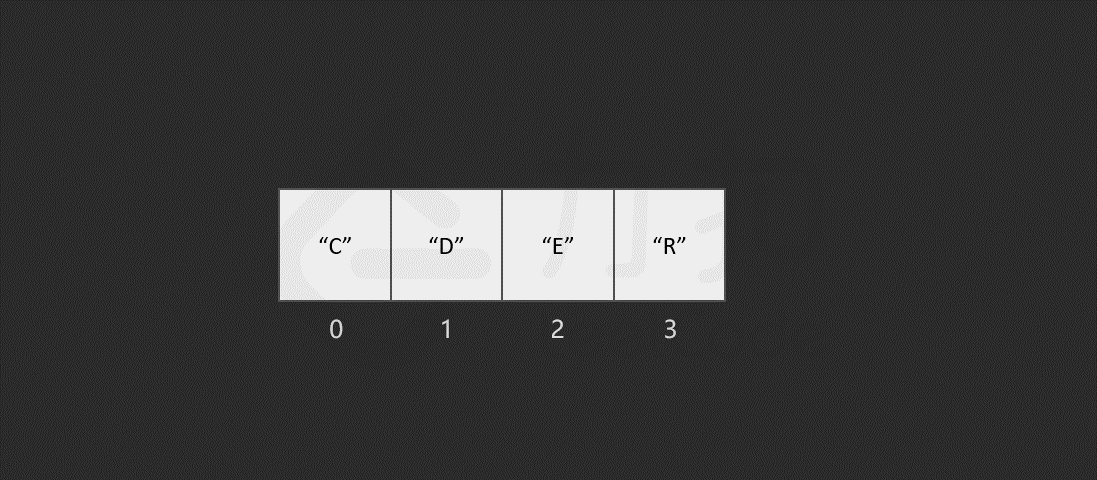
当数组的长度为 n 时,最坏情况下,我们删除第一个元素,共需要的步骤数为 1 + (n - 1) = n 步,其中,1 为删除操作,n - 1 为移动其余元素的步骤数。删除操作具有线性时间复杂度,即时间复杂度为 O(N)O(N)O(N),NNN 为数组的长度。
编程练习
寻找数组的中心索引
给定一个整数类型的数组 nums,请编写一个能够返回数组 “中心索引” 的方法。
我们是这样定义数组 中心索引 的:数组中心索引的左侧所有元素相加的和等于右侧所有元素相加的和。
如果数组不存在中心索引,那么我们应该返回 -1。如果数组有多个中心索引,那么我们应该返回最靠近左边的那一个。
示例 1:
输入:
nums = [1, 7, 3, 6, 5, 6]
输出:3
解释:
索引 3 (nums[3] = 6) 的左侧数之和 (1 + 7 + 3 = 11),与右侧数之和 (5 + 6 = 11) 相等。
同时, 3 也是第一个符合要求的中心索引。
示例 2:
输入:
nums = [1, 2, 3]
输出:-1
解释:
数组中不存在满足此条件的中心索引。
说明:
nums 的长度范围为 [0, 10000]。
任何一个 nums[i] 将会是一个范围在 [-1000, 1000]的整数。
思路:
左边部分初始值为 0
初始索引为 0
右边部分的初始值是从下标为 1 开始的和
每一轮循环, 判断 leftPartSum 是否等于 rightPartSum
相等则返回索引 i
不相等,此时索引 i 变成 i + 1, 所以 leftPartSum = leftPartSum + nums[i], rightPartSum = rightPartSum - nums[i+1]
代码演示:
/**
* @param {number[]} nums
* @return {number}
* 测试数组为[1,7,3,6,5,6]
*/
var pivotIndex = function (nums) {
if (nums.length === 0) {
return -1
}
if (nums.length === 1) {
return 0
}
// 初始索引为 0, 计算索引两边的和, 右边部分的和可以通过 reduce 计算
let leftPartSum = 0
let rightPartSum = nums.slice(1).reduce((sum, num) => sum += num, 0)
for (let i = 0; i < nums.length; i++) {
if (leftPartSum === rightPartSum) {
return i
}
leftPartSum += nums[i]
if (nums[i + 1]) {
rightPartSum -= nums[i + 1]
}
}
return -1
};