mamacher算法（回文字符）

题目地址 ：http://acm.hdu.edu.cn/showproblem.php?pid=3068。

给出一个只由小写英文字符a,b,c...y,z组成的字符串S,求S中最长回文串的长度. 
回文就是正反读都是一样的字符串,如aba, abba等

Input输入有多组case,不超过120组,每组输入为一行小写英文字符a,b,c...y,z组成的字符串S 
两组case之间由空行隔开(该空行不用处理) 
字符串长度len <= 110000Output每一行一个整数x,对应一组case,表示该组case的字符串中所包含的最长回文长度. 
Sample Input

aaaa

abab

Sample Output

4
3

题目大意 ： 找到字符串中，回文的最大长度。

题目分析 ：我们从最简单的想法开始理解题目要用以很多，所以我先讲一下，最普遍的思维，再重这个思维上讲到今天要讲的mamacher算法。最简单的想法就是循环遍历，从当前

位置 i 向两边查找并记录这个位置可以向两侧延伸的最大值Len[i]。
        


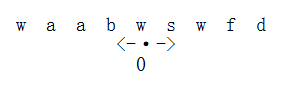
直到查找完毕后，我们将Len[i]*2+1得到回文串的大小。我们想一下这样就完了？很可惜，我们还没有完成，是哪里错了呢？
我们来举个例子：
   
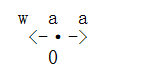
咦，我们的结果最后不应该是2吗？但是公式得到的答案确实0，哪里出问题了啊！
我们再来看个例子：

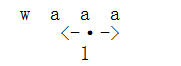
哦，这个有对了，对比之后，我想你已经得到答案了。是的，由于奇数的性质，我们无法得到最后为偶数个回文数的正确答案，而且还有溢出的风险。那好吧，我们就分奇偶来讨论，这

样问题不就解决了吗？这里我就不给出它的代码了，大家可以自己去错分奇偶试试。到了这一步，我们只需要分析，算法的时间复杂度是否能在规定时间內完成了。本代码的时间复杂度

O(m*m),取最坏情况，假设我们每一次都要向两侧循环105，那总次数就我105*105=1010，按道理来说，2秒时间完全胜任这样的计算量，但是我没这样写，而是用来接下来的mamacher

算法来快速查找。

****************************************************************************************************************************************
在之前我们遇到了错分奇偶的情况，那我们有没有办法消除这种情况呢？答案是有的，我们在每一个数的中间添加一个分隔符，这样无论奇偶都变成了偶数的了，那我们分析起来也就方便

了。没了奇偶之分，难道还用老方法遍历？肯定不会啦。

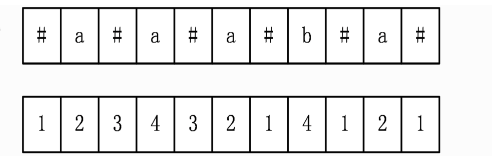这里提供一个模板。

我们来看看一个图片：（难度有点大，要反反复复推敲）


我先来解释 mx，mx是记录了当前我们得到的回文的最大长度的位置，id就是当前最大回文的中间值。i是我们循环时我们要查找回文的中间值（也就是上文说遍历，从i向两边延伸）,p[]是辅

助数组，记录值的大小。

接下来核心分析：

if（i>mx)，当你的i值超过了mx，说明i的两侧你并没有查找过，我们就只有乖乖的一个一个像上面一样老老实实的查找。

if（i<mx), 当i的位置还在最大回文的内部，我们知道回文翻过来还是回文，也就是说i的对称点j的回文应该和i的回文一样。

　　　　　　if（mx-i>p[j])的话，mx-i表示i达到的回文大小，p[j]查找的到回文大小（大小已经固定），说明p[i]的回文全部在当前最大回文的内部，我们只要取min(p[j],mx-i)即可。

　　　　　　if（mx-i<=p[j]),p[i]的回文可能超过了mx，而mx我们还没有查找过，这就需要我们去查找了。


核心代码：

void mamacher()
{
    int mx=0,id;
    for(int i=1;i<os.size();i++)
    {
        if(mx>i)
            pi[i]=min(pi[2*id-i],mx-i);
        else
            pi[i]=1;
        while(os[pi[i]+i]==os[i-pi[i]])//查找相同的。
            Len[i]++;
        if(i+pi[i]>mx)
        {
            id=i;
            mx=i+pi[i];
        }
    }
}

本题ac代码 ：

#include <iostream>
#include <cstdio>
#include <cstring>
#include <string>
#include <algorithm>
const int maxn=1e6+5;
using namespace std;
string s,os;
int Len[maxn*2],len;


void getstr()
{
    os+='$';
    for(int i=0;i<s.size();i++)
    {
        os+='#';
        os+=s[i];
    }
    os+='#';
}

void mamacher()
{
    getstr();
    int mx=0,id;
    for(int i=1;i<os.size();i++)
    {
        if(mx>i)
            Len[i]=min(Len[2*id-i],mx-i);
        else
            Len[i]=1;
        while(os[Len[i]+i]==os[i-Len[i]])
            Len[i]++;
        if(i+Len[i]>mx)
        {
            id=i;
            mx=i+Len[i];
        }
    }
}

int main()
{
   while(cin >>s)
   {
        memset(Len,0,sizeof(Len));
        mamacher();
        int sum=1;
        for(int i=1;i<os.size();i++)
        {
            if(Len[i]>sum)
                sum=Len[i];
        }
        cout << sum-1 <<endl;
        s.clear(),os.clear();
   }
}