棋盘

我讲的题却并不想写博客...
原题:屠龙宝刀点击送
题面:
有一个(m×m)的棋盘，棋盘上每一个格子可能是红色、黄色或没有任何颜色的。你现在要从棋盘的最左上角走到棋盘的最右下角。
任何一个时刻，你所站在的位置必须是有颜色的（不能是无色的）， 你只能向上、 下、左、 右四个方向前进。当你从一个格子走向另一个格子时，如果两个格子的颜色相同，那你不需要花费金币；如果不同，则你需要花费 1 个金币。
另外， 你可以花费 2 个金币施展魔法让下一个无色格子暂时变为你指定的颜色。但这个魔法不能连续使用， 而且这个魔法的持续时间很短，也就是说，如果你使用了这个魔法，走到了这个暂时有颜色的格子上，你就不能继续使用魔法； 只有当你离开这个位置，走到一个本来就有颜色的格子上的时候，你才能继续使用这个魔法，而当你离开了这个位置（施展魔法使得变为有颜色的格子）时，这个格子恢复为无色。
现在你要从棋盘的最左上角，走到棋盘的最右下角，求花费的最少金币是多少？

这题就是深搜,代码:

#include<iostream>
#include<cstdio>
using namespace std;
int mx[5]={0,-1,0,1,0};
int my[5]={0,0,1,0,-1};
int n,m;
int col[105][105];
bool vis[105][105];
int ans=0x3fffffff;
inline void search(const int &x,const int &y,int step,bool used){
    if(x==m&&y==m){
        ans=ans<step? ans:step;
        return;
    }
    for(int i=1;i<=4;i++){
        int nx=x+mx[i];
        int ny=y+my[i];
        if(nx<1||nx>m||ny<1||ny>m||vis[nx][ny]) continue;
        if((!col[nx][ny])&&(used)) continue;
        if((!col[nx][ny])&&(!used)){
            vis[nx][ny]=1;
            col[nx][ny]=col[x][y];
            search(nx,ny,step+2,1);
            col[nx][ny]=0;
            vis[nx][ny]=0;
        }
        else if(used){
            if(col[nx][ny]==col[x][y]){
                col[x][y]=0;
                vis[nx][ny]=1;
                search(nx,ny,step,0);
                vis[nx][ny]=0;
            }
            if(col[x][y]!=col[nx][ny]){
                col[x][y]=0;
                vis[nx][ny]=1;
                search(nx,ny,step+1,0);
                vis[nx][ny]=0;
            }
        }
        else if(col[nx][ny]==col[x][y]){
            vis[nx][ny]=1;
            search(nx,ny,step,0);
            vis[nx][ny]=0;
        }
        else if(col[x][y]!=col[nx][ny]){
            vis[nx][ny]=1;
            search(nx,ny,step+1,0);
            vis[nx][ny]=0;
        }
    }
}
int main(){
    scanf("%d%d",&m,&n);
    for(int i=1;i<=n;i++){
        int a,b,c;
        scanf("%d%d%d",&a,&b,&c);
        col[a][b]=c+1;
    }
    vis[1][1]=1;
    search(1,1,0,0);
    if(ans<0x3fffffff)
        printf("%d",ans);
    else
        printf("-1
");
    return 0;
}

然后你愉快地发现:


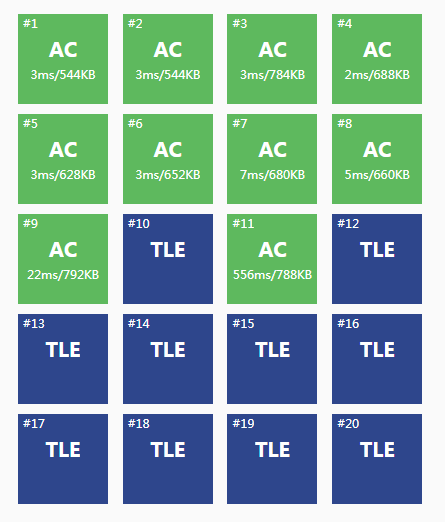
发现你的效率并不够高,需要剪枝加记忆化,
首先看以上代码,很好理解,就结合以上代码谈谈改进:
1.添加记忆化,把每个点的最优状态保存,一旦发现当前搜索状态不如之前优或者一样优就剪掉,没啥用,并且可以免去(vis)(有没有访问过)这个(bool)数组,免去重复访问,自己证明正确性去
2.改掉了繁杂的判断,每次使用"膜法"的时候回改变无色格子状态,同样用记忆化来免去重复访问,不用担心无色格子什么时候变回去.
3.(search)函数递归更加清爽整洁.
4.没了,再水一行.
注意:
1.每次状态要赋个极大值,不然怎么判断记忆化最优?
2.其实判断当前函数无色那一句不用加,因为递归保证不会踩到无色格子
3.(nx)与(ny)不能在(search)函数外定义,会引起递归错误,
4.这题(n)和(m)的意义要搞清楚,
5.没了,又水一行
这里的"注意"是我给别人调程序时的经验,当然也算收获辣~(≧▽≦)/~
AC代码:

#include<iostream>
#include<cstdio>
#include<cstring>
using namespace std;
int mx[5]={0,-1,0,1,0};
int my[5]={0,0,1,0,-1};
int n,m;
int col[105][105];
int stp[105][105];
int ans=0x3fffffff;
inline void search(int x,int y,int step,bool used){
    if(x<1||x>m||y<1||y>m) return;
    if(!col[x][y]) return;
    if(step>=stp[x][y]) return;
    stp[x][y]=step;
    if(x==m&&y==m){
    	if(ans>step) ans=step;
    	return ;
    }
    for(int i=1;i<=4;i++){
        int nx=x+mx[i];
        int ny=y+my[i];
        if(col[nx][ny]){
            if(col[nx][ny]==col[x][y])
                search(nx,ny,step,0);
            else
                search(nx,ny,step+1,0);	
        }else if(!used){
            col[nx][ny]=col[x][y];
            search(nx,ny,step+2,1);
            col[nx][ny]=0;
        }
    }
}
int main(){
    memset(stp,63,sizeof(stp));
    scanf("%d%d",&m,&n);
    for(int i=1;i<=n;i++){
        int a,b,c;
        scanf("%d%d%d",&a,&b,&c);
        col[a][b]=c+1;
    }
    search(1,1,0,0);
    if(ans<0x3fffffff)
        printf("%d",ans);
    else
        printf("-1
");
    return 0;
}