T1:地精部落

题目大意:
定义中间大临靠的两边小的山峰,反之为山谷,求出一半峰一半谷的序列个数
思路1:暴力((20pts-40pts))
开题一看,又是排列问题,而且
全排列+打表搞它
代码:
int main(){
n=read(),mol=read();
for(int i=1;i<=n;i++)a[i]=i;
do{
int flag=1;
for(int i=2;i<n;i++){
if((a[i-1]<a[i]&&a[i]<a[i+1])||(a[i-1]>a[i]&&a[i]>a[i+1])){flag=0;break;}
}
ans+=flag;
}while(next_permutation(a+1,a+1+n));
cout<<ans%mol;
return 0;
}
思路2:(DP)((100pts))
像这种排列方面的问题,而且是只给了数列大小的题,不是打表找规律就是贪心过样例n方DP,区别就看数据范围
一看就是神仙做的: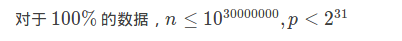
一看就是(O(1))的组合数或矩阵加速的(一般(n)直接开(1e18)了):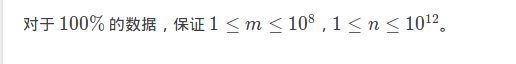
一看就是(DP)的:
放错图了: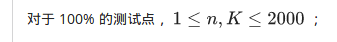
好了,回归正题
一看就很组合数+(DP),设定(f_{i,0/1})表示长度为(i)且开头是山谷或山峰的合法序列。现在有以下几个性质:
-
性质1:(1-k)的合法序列和(x+1-x+k+1)的合法序列方案数一致
- 证明:可以直接把(x+1-x+k+1)整体减去(x),这样就得到了(1-k)的合法序列
-
性质2:合法序列长度为奇数时,若首元素为山谷,则尾元素也为山谷;若首元素为山峰,则尾元素也为山峰。合法序列长度为偶数时,若首元素为山谷,则尾元素也为山峰;若首元素为山峰,则尾元素也为山谷
- 证明:动手画一下就行
所以我们可以用脚得出状态转移方程:
[f_{i,0}=sum f_{j,0}×f{i-j-1}×C_{i-1}^j(j\%2==1)
]
[f_{i,1}=sum f_{j,1}×f{i-j-1}×C_{i-1}^j(j\%2==0)
]
我们考虑把第(i)个元素,即数字(i)插入到前面的序列中,可以以插入的位置为断点,考虑左右两个序列。根据性质1和性质2可以直接得出转移方程。后面组合数代表前(i-1)个元素,选出(j)个元素放在断点左边,其它的放在断点右边,因为枚举了第一个元素是山峰或山谷,只有当断点左右都是山谷时才能插入,所以转移一定合理
代码:
int main(){
n=read();mol=read();
c[1][0]=c[1][1]=1;
for(int i=2;i<=n;i++){
c[i][0]=1;
for(int j=1;j<=i;j++){
c[i][j]=(c[i-1][j-1]+c[i-1][j])%mol;
}
}
f[0][0]=f[0][1]=f[1][0]=f[1][1]=1;
for(int i=2;i<=n;i++){
for(int j=0;j<i;j++){
if(j&1)f[i][0]=(f[i][0]+f[j][0]*f[i-j-1][0]%mol*c[i-1][j]%mol)%mol;
else f[i][1]=(f[i][1]+f[j][1]*f[i-j-1][0]%mol*c[i-1][j]%mol)%mol;
}
}
cout<<(f[n][0]+f[n][1])%mol;
return 0;
}
思路3:优化((100pts))
对于上面的性质,我们可以扩展出第三条:
- (f_{i,0}=f_{i,1})
- 证明:很简单,把原序列翻过来就行了
所以可以直接把第二维压掉
代码:
int main(){
n=read();mol=read();
c[1][0]=c[1][1]=1;
for(int i=2;i<=n;i++){
c[i][0]=1;
for(int j=1;j<=i;j++){
c[i][j]=(c[i-1][j-1]+c[i-1][j])%mol;
}//这里也可以滚动数组放在下面,省点空间
}
f[0]=1;f[1]=1;
for(int i=2;i<=n;i++){
for(int j=0;j<i;j++){
if(j&1)f[i]=(f[i]+1LL*f[j]*f[i-j-1]%mol*c[i-1][j]%mol)%mol;
}
}
cout<<f[n]*2%mol;
return 0;
}