本文主要为机器学习基础
训练,验证,测试 集
一般6,2,2,如果测试有100万数据,也可以98:1:1,确保来自于同一分布
欠拟合,过拟合,适度拟合
如果训练集误差1%,验证集11%,过拟合,称为“高方差”如果训练集15%,验证集16%,称为“高偏差”,可能两个都有也可能两个都没有
正则化:
高方差解决方法:正则化和更多数据,即预防过拟合
通常只正则化w,因为参数b影响不大。
通常是L2正则化,也有L1正则化,加的参数不同L1会使w变稀疏(然而好像没什么用)所以现在都用 L2
“弗罗贝尼乌斯范数”,它表示一个矩阵中所有元素的平方和,可能被用于梯度下降,是L2正则化中用到的
dropout正则化(随机失活),实施方法有几种 ,这里重点讲inverted dropout(反向随机失活)与之对比的是keep-prob,值为1时drop无效
Dropout可以随机删除网络中的神经单元,可以通过正则化发挥较大的作用。因为其通过传播所有权重,产生收缩权重的平方范数的效果
因为所有的单神经元都有可能被随机清除,因而其权重不会过大。

第二个权重矩阵是7*7的,是最大的,因而为了预防过拟合,它的keep-prob最低如0.5,其它层0.7不担心的如2*3,1*2的为1.。但开启dropout代价函数J不再被明确定义,每次迭代,都会随机移除一些节点,如果再三检查梯度下降的性能,实际上是很难进行复查的。
归一化:防止代价函数图形狭长
梯度消失/梯度爆炸:
在深度神经网络中,激活函数将以指数级递减,虽然我只是讨论了激活函数以与相关的指数级数增长或下降,它也适用于与层数L相关的导数或梯度函数,也是呈指数级增长或呈指数递减。
梯度检验
此方法只用于调试,且梯度检验不能与dropout一起用
把所有参数转换成一个巨大的向量数据,
如何定义两个向量是否真的接近彼此?我一般做下列运算,计算这两个向量的距离,欧几里得范数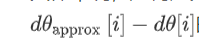
它是误差平方之和,然后求平方根,得到欧式距离,然后用向量长度归一化,使用向量长度的欧几里得范数。如果ε为10-7,误差在此之内,就比较好,10-5,需要检查,10-3应仔细检查所有项