边端问题的两类题型
①植树问题
②方阵问题
线性植树:(两端不封闭)
棵树 = 总长 ÷ 间距 + 1(算头算尾要加一)(总长 ÷ 间距 求出的是空数。100÷20=5个空)
总长 = (棵树 - 1 )× 间距 (棵树比空数多一个。所以要减一)
环形植树:
棵树 = 总长 ÷ 间距 (棵树 = 空数)
楼间植树:(两栋楼之间植树,相当于少了头尾两颗)
棵树 = 总长 ÷ 间距 - 1 (不算头不算尾要减少一)
方阵问题:
每边人数 = 4边总人数÷ 4 + 1
方阵的外层比里层每边多2人。
方阵的外层比里层共多8人。
例题:
S01:某机构计划在一块边长为18米的正方形空地开展活动,需要在空地四边每隔2米插上一面彩旗,若该空地的四个角都需要插上彩旗,那么一共需要( )面彩旗。
A. 32 B. 36 C. 44 D. 48
S02:参加某运动会的全体运动员在开幕式上恰好排成一个正方形,有两行两列的运动员离场后,运动员人数减少64人,则参加该运动会的运动员人数为:
A . 225 B . 256 C . 289 D . 324
思路:
两行两列要理解成最外圈的人。64÷4 + 1= 17*17 = 289
L01:某条道路进行灯光增亮工程,原来间隔35米的路灯一共有21盏,现要将路灯的间隔缩短为25米,那么有( )盏路灯无需移动。
A. 2 B. 3 C. 4 D. 5
思路:
不需移动的位置就是最小公倍数的位置,求最小公倍数
700÷175 + 1 = 5
L02:有绿、白两种颜色且尺寸相同的正方形瓷砖共400块。将这些瓷砖铺在一块正方形的地面上:最外面的一周用绿色瓷砖铺,从外往里数的第二周用白色瓷砖铺,第三周用绿色瓷砖,第四周用白色瓷砖……这样依次交替铺下去,恰好将所有瓷砖用完。这块正方形地面上的绿色瓷砖共有( )块。
A.180 B.196 C.210 D.220
思路:
400 = 20 * 20 ,这是一个20*20的正方形,最外层一共有20*4-4 = 76块砖。
最外层和里层差8块,76 -> 口 -> 60 -> 44 -> 28 -> 12 ,相当于公差是16的等差数列。44*5 = 220
补充:
等差数列求和: , 首项末项的平均数
, 首项末项的平均数
求项数n: ,
,

等比数列求和:
求项数n: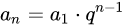
自然数列:1+2+...+n = n×(n+1) ÷2
G01:一条笔直的林荫道两旁种植着梧桐树,同侧道路每两棵梧桐树间距50米。林某每天早上七点半穿过林荫道步行去上班,工作地点恰好在林荫道尽头。经测试,他每分钟步行70步,每步大约50厘米,每天早上八点准时到达工作地点。那么,这条林荫道两旁栽种的梧桐树共有多少棵?
A.21 B.22 C.42 D.44
思路:
70*0.5*30 = 1050米,1050÷50 + 1 = 22 *2 = 44
G02:某高中学校举行运动会,高一、高二、高三学生列成方队,每个年级队伍均为240人,分成6个竖列依次行进。高一队伍前后每人间隔1米,高二队伍前后每人间隔1.5米,高三队伍前后每人间隔2.5米。每个年级队伍之间间隔5米,所有年级队伍的行进速度均为60米每分钟,则三个年级队伍通过35米长的主席台需要( )分钟。
A.3 B.4 C.5 D.6
思路:
通过主席台 = 队伍长度 + 主席台长度
40人 39个人空 -> (39*1 + 39*1.5 + 39*2.5 + 2*5 + 35) ÷ 60
母题研究:
1、某单位两座办公楼之间有一条长204米的道路,在道路起点的两侧和终点的两侧已栽种了一棵树。现在要在这条路的两侧栽种更多的树,使每一侧每两棵树之间的间隔不多于12米。如栽种每棵树需要50元人工费,则为完成栽种工作,在人工费这一项至少需要做多少预算?
A.800元 B.1600元 C.1700元 D.1800元
思路:
楼间植树问题,204÷12 - 1 = 17 -1 =16
2、李大爷在马路边散步,路边均匀地栽着一行树,李大爷从第一棵树走到第15棵树共用了7分钟,李大爷又向前走了几棵树后就往回走,当他回到第5棵树时共用了30分钟。李大爷步行到第几棵树时就开始往回走?
A.32 B.35 C.34 D.33
思路:
第一棵走到第15棵一共有14个空,花了7分钟,所以1分钟走2个空。
从第一棵树走到第x棵树,再从第x棵树走到第5棵树。
走了 x-1个空 + x-5 个空。 (x-1)+(x-5) = 60 ,得x=33
3、环保部门对一定时间内的河流水质进行采样,原计划每41分钟采样1次,但在实际采样过程中,第一次和最后一次采样的时间与原计划相同,每两次采样的间隔变成20分钟,采样次数比原计划增加了1倍。问实际采样次数是多少次?
A.22 B.32 C.42 D.52
思路:
原计划每41分钟采样1次 = 间隔41米一棵树 ,第一次和最后一次采样的时间与原计划相同 = 马路长度不变,变成20米一棵树
X - 1 = 空数,(X - 1) × 41 = (2X -1) × 20
4、某条道路的一侧种植了25棵杨树,其中道路两端各种有一棵,且所有相邻的树距离相等。现在需要增种10棵树,且通过移动一部分树(不含首尾两棵)使所有相邻的树距离相等,则这25棵树中有多少棵不需要移动位置?
A.3 B.4 C.5 D.6
思路:
25棵树 = 24个空,35棵树 = 34个空
设马路长度 为24与34最小公倍数 = 408米。
17米每棵,12米每棵。最小公倍数204米。408÷204 + 1 = 3
5、施工队要在一东西长600米的礼堂顶部沿东西方向安装一排吊灯,根据施工要求,必须在距西墙375米处安装一盏,并且各吊灯在东西墙之间均匀排列(墙角不能装灯)。该施工队至少需要安装多少盏吊灯?
A.6 B.7 C.8 D.9
思路:
求375与225最大公约数:75。
楼间植树问题 = 600 ÷ 75 -1