第71课 图的定义

1. 图的定义

（1）定义：图是由顶点集合（Vertex）及顶点间的关系集合（Edge）组成的一种数据结构。Graph = (V, E); 其中：

　　V={x|x∈某个数据对象}是顶点的有穷非空集合

　　E={(x,y)}x, y∈V}是顶点之间关系（边）的有穷集合

 

（2）比较线性表、树和图的不同

	数据元素 的名称	数据对象 （数据元素的集合）	数据元素 之间的关系
线性表	元素	无元素为空表	线性关系
树	结点	无结点的为空树	层次关系
图	顶点（Vertex）	顶点集有穷非空	边（边集可为空）

2. 相关概念

 

（1）无向边和无向图

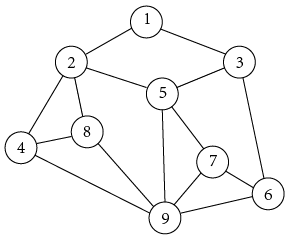
　　①无向边：若顶点x和y之间的边没有方向，称边(x，y)为无向边（注意，用圆括号表示）。可见，(x,y)和(y,x)的意义相同，表示x和y之间有连接，x和y互为邻接点(adjacent)。

　　②无向图：任意两个顶点之间的边均为无向边的图，称为无向图（Undirected Graph）。如图G1={V,{E}}，其中顶点集V={A,B,C,D}，边集E={(A,B),(B,C),(C,D),(D,A),(A,C)}

（2）有向边和有向图

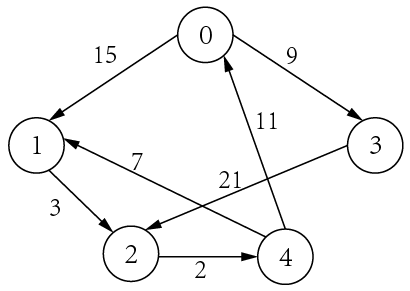
　　①有向边：若顶点x和y之间的边有方向，称边<x,y>称为有向边或弧(Arc)（注意：用尖括号表示）。可见，<x,y>和<y,x>意义不同，表示x连接到y。x为弧尾（Tail),y为弧头(Head）

　　②有向图：任意两个顶点之间的边均为有向边的图，称为有向图（Directed Graph）。对于有向图G={V,{E}}，其中顶点集V={A,B,C,D} ,边集E={<A,D>,<B,A>,<B,C>,<C,A>}

（3）顶点的度

　　①入度（InDegree）：以v为头的边的数目，记为ID(v)。入度是针对有向图的，如图G2图中A的入度为2。

　　②出度（OutDegree）：以v为尾的边的数目，记为OD(v)。出度也是针对有向图的，如图G2中A的出度为1。

　　③顶点的度：顶点v的度是和v相关联的边的数目，记为TD(v)。适用于无向图和有向图，对于有向图而言TD(v)=ID(v)+OD(v)。

　　④顶点和边的关系

顶点度数	TD(v) = ID(v) + OD(v)	顶点度数=入度+出度
边数	E=[TD(v1)+TD(v2)+…+TD(vn)]/2	边数=总度数/2
	E=ID(v1)+ID(v2)+…+ID(vn)	边数=总入度
	E=OD(v1)+OD(v2)+…+OD(vn)	边数=总出度

（4）权（weight）：与图的边相关的数字，可以表示顶点间的距离或耗费。

 

3. 图的操作

 

（1）常见的操作：①获取/设置顶点的值；②获取邻接顶点；③获取/设置边的值。④删除边；⑤获取顶点数/边数；⑥获取顶点的度数；⑦判断是否为无向图，等等。

【编程实验】图的抽象类创建

#ifndef _GRAPH_H_
#define _GRAPH_H_

#include "Object.h"
#include "SharedPointer.h"
#include "Array.h"

namespace DTLib
{

//V为顶点类型，E为边类型
template<typename V, typename E>
class Graph : public Object
{
public:
    virtual V getVertex(int i) = 0;
    virtual bool getVertex(int i, V& value) = 0;
    virtual bool setVertex(int i, const V& value) = 0;

    //获取顶点i的邻接顶点
    virtual SharedPointer<Array<int> > getAdjacent(int i) = 0;

    //参数i为起点、j为终点、value为边(权值)
    virtual E getEdge(int i, int j) = 0;
    virtual bool getEdge(int i, int j, E& value) = 0;
    virtual bool setEdge(int i, int j, const E& value) = 0;
    virtual bool removeEdge(int i, int j) = 0;

    //判断是否可看做无向图
    bool asUndirected()
    {
        bool ret =true;

        for(int i=0; i<vCount() && ret; i++){
            for(int j=0; j<vCount() && ret; j++){
                //判断i和j互为邻接顶点且<i,j>和<j,i>边的权值相等
                if(isAdjacent(i, j)){
                    ret = ret && isAdjacent(j, i) && (getEdge(i, j) == getEdge(j, i));
                }
            }
        }

        return ret;
    }

    //判断图中顶点i到顶点j是否邻接
    virtual bool isAdjacent(int i, int j) = 0;

    virtual int vCount() = 0; //获取顶点的数量
    virtual int eCount() = 0; //获取边的数量

    virtual int OD(int i) = 0; //获取顶点i的出度
    virtual int ID(int i) = 0; //获取顶点i的入度
    virtual int TD(int i) //获取顶点i的度
    {
        return ID(i) + OD(i);
    }
};

}

#endif // _GRAPH_H_

4. 小结

（1）图是顶点与边的集合，是一种非线性的数据结构

（2）图中顶点可以与多个其它顶点产生邻接关系

（3）边的权值，用于表示顶点间的距离。

（4）图在程序中表现为特殊的数据类型