【学习笔记】强连通分量之 Tarjan

引言

何为强连通分量？

强连通分量是指在一张 有向图 中的几个极大点集，使得每一个点集里的任意两个点存在双向连通路径。

举个，下面这个有向图里有三个强连通分量，分别用红圈圈起来了：

而 Tarjan 就是求解强连通分量的算法之一，复杂度与输入成正比，即 (Theta(n+m))。

算法讲解

首先，我们应该怎么求强连通分量？

我们应该要回到定义：「里面任意两点存在双向连通路径。」

Tarjan 算法的核心就是利用 DFS 建立树状关系，从而可以快速求解强连通分量。

首先，我们有什么方法可以快速判定强连通的存在呢？显然就是可以回到自己本身。

同时，只要自己能够到达的点中有一部分能够回到自己，就构成了一个强连通块。

---

那么，我们又如何能够求出强联通 分量 呢？

只要利用其极大特性，我们不难想到树形结构。因为树满足严格的从属关系并且可以做到极大。

所以，我们构造一棵 有向 搜索树，并利用剩余的边来求解强连通分量。

---

为了满足其极大性，判定强连通应在强连通分量的深度最高处。

同时，为了快速求出节点回到得最小值，我们引入一些概念：

• dfn：DFS 序，可以比较前后关系。
• low：能到达的最低 DFS 序的节点编号。这可以通过 DP 求出。

显然，我们可以通过 DFS 的方式构建一棵搜索树，并求出 dfn 和 low 数组。

同时，一个节点的子树内的所有节点的 low 显然大于等于这个节点的 low，否则这个节点的 low 就不对了。

根据这点性质，选在同一个强连通分量里的节点必然有相同的 low 值，并且分布是「子树砍脚」，也就是说块状。

我们考虑用一个栈来维护这样的结构。按照 DFS 时间戳入栈，并在找到强连通分量以后出栈。

---

以上就是 Tarjan 求强连通分量的核心内容。接下来，比较需要注意的是那些不属于搜索树的一些边。我们可以分为两类：

• 返回边：如下图红色。指向起始节点的祖先。
• 横叉边：如下图蓝色。不是返回边的不属于搜索树的边。

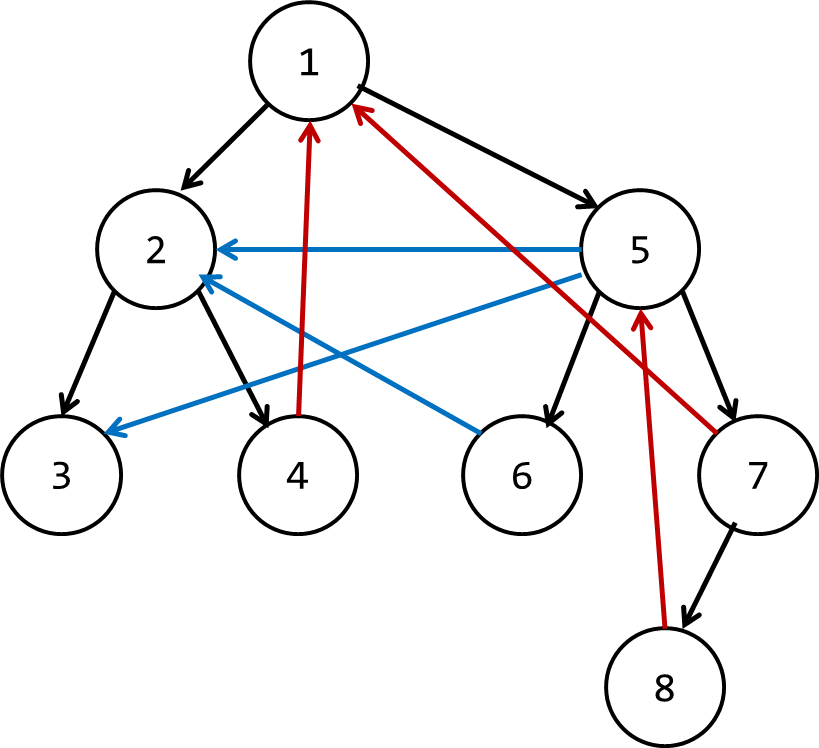
我们可以干眼瞎瞅出一些性质来：

• 横叉边必然是大号指向小号，否则必然就会成为搜索树上的一条边。
• 任何强连通分量必然 不包含 横叉边，即去掉所有横叉边必然不影响连通性。

这一点在 Code 的时候还是很需要在意的。否则可能会出一点问题。

顺带提一句，使用 Tarjan 求出强连通分量以后就可以进行缩点，使其变成一个 DAG。方法就是建一张新的图，并枚举所有的边。

模板代码

这里只给出核心代码，具体内容自行理解。

/*
数组、变量解释：

ids: 栈；
tim: 时间戳；
dfn[i],low[i]: 已解释；
hd[i],des[i],nxt[i]: 邻接表；
ins[i]: 是否在栈中；
bel[i]: 所属于的强连通分量编号。
*/

void tarjan(int id)
{
	int tmp;
	
	dfn[id] = tim++, low[id] = dfn[id], ins[id] = true;
	ids.push(id);
	
	for (int p = hd[id]; p != -1; p = nxt[p])
	{
		if (dfn[des[p]] == -1)
		{
			tarjan(des[p]);
			low[id] = my_min(low[id], low[des[p]]);
		}
		else if (ins[des[p]])
			low[id] = my_min(low[id], low[des[p]]);
	}
	
	if (low[id] == dfn[id])
	{
		while (!ids.empty())
		{
			tmp = ids.top();
			ids.pop();
			
			ins[tmp] = false;
			bel[tmp] = scc_cnt;
                        
			if (tmp == id)
				break;
		}
		
		scc_cnt++;
	}
}

例题

模板（Added 缩点，拓扑排序，DP）

就是一道中规中矩的模板题。比较考验综合码力。

Code：

#include <stack>
#include <queue>
#include <cstdio>
#include <cctype>
#include <cstring>
using namespace std;

const int max_n = 10000, max_m = 100000;

int hd[max_n], des[max_m], nxt[max_m], node_val[max_n], bel[max_n], edge_cnt = 0;
int dfn[max_n], low[max_n], nval[max_n] = {}, dp[max_n] = {}, tim = 0, scc_cnt = 0;
int nhd[max_n], ndes[max_m], nnxt[max_m], ind[max_n] = {}, ord[max_n] = {}, neg_cnt = 0;
bool ins[max_n] = {};

stack<int> ids;

inline int my_min(int a, int b) { return (a < b)? a:b; }
inline int my_max(int a, int b) { return (a > b)? a:b; }

inline int read()
{
	int ch = getchar(), n = 0, t = 1;
	while (isspace(ch)) { ch = getchar(); }
	if (ch == '-') { t = -1, ch = getchar(); }
	while (isdigit(ch)) { n = n * 10 + ch - '0', ch = getchar(); }
	return n * t;
}

void add_edge(int s, int t)
{
	des[edge_cnt] = t;
	nxt[edge_cnt] = hd[s];
	hd[s] = edge_cnt++;
}

void nadd_edge(int s, int t)
{
	ndes[neg_cnt] = t;
	nnxt[neg_cnt] = nhd[s];
	nhd[s] = neg_cnt++;
}

void tarjan(int id)
{
	int tmp;
	
	dfn[id] = tim++, low[id] = dfn[id], ins[id] = true;
	ids.push(id);
	
	for (int p = hd[id]; p != -1; p = nxt[p])
	{
		if (dfn[des[p]] == -1)
		{
			tarjan(des[p]);
			low[id] = my_min(low[id], low[des[p]]);
		}
		else if (ins[des[p]])
			low[id] = my_min(low[id], low[des[p]]);
	}
	
	if (low[id] == dfn[id])
	{
		while (!ids.empty())
		{
			tmp = ids.top();
			ids.pop();
			
			ins[tmp] = false;
			bel[tmp] = scc_cnt;
			nval[bel[tmp]] += node_val[tmp];
			
			if (tmp == id)
				break;
		}
		
		scc_cnt++;
	}
}

int main()
{
	memset(hd, -1, sizeof(hd));
	memset(bel, -1, sizeof(bel));
	memset(dfn, -1, sizeof(dfn));
	memset(nhd, -1, sizeof(nhd));
	
	int n = read(), m = read(), ta, tb, lp = 0, rp = 0, ans = 0;
	
	for (int i = 0; i < n; i++)
		node_val[i] = read();
	for (int i = 0; i < m; i++)
	{
		ta = read(), tb = read();
		add_edge(ta - 1, tb - 1);
	}
	
	for (int i = 0; i < n; i++)
		if (dfn[i] == -1)
			tarjan(i);
	
	for (int i = 0; i < n; i++)
		for (int p = hd[i]; p != -1; p = nxt[p])
			if (bel[i] != bel[des[p]])
			{
				nadd_edge(bel[i], bel[des[p]]);
				ind[bel[des[p]]]++;
			}
	
	memset(ins, false, sizeof(ins));
	
	for (int i = 0; i < scc_cnt; i++)
		if (!ind[i])
		{
			ord[rp++] = i;
			ins[i] = true;
		}
	
	while (lp != rp)
	{
		ta = ord[lp++];
		
		for (int p = nhd[ta]; p != -1; p = nnxt[p])
		{
			ind[ndes[p]]--;
			
			if (!ind[ndes[p]] && !ins[ndes[p]])
			{
				ins[ndes[p]] = true;
				ord[rp++] = ndes[p];
			}
		}
	}
	
	for (int i = rp - 1; i >= 0; i--)
	{
		tb = 0;
		for (int p = nhd[ord[i]]; p != -1; p = nnxt[p])
			tb = max(tb, dp[ndes[p]]);
		
		dp[ord[i]] = tb + nval[ord[i]];
		ans = max(ans, dp[ord[i]]);
	}
	
	printf("%d
", ans);
	
	return 0;
}

---

稳定婚姻

这是一道很经典的 Tarjan 练手题，思路也比较简单。

明显地，如果去掉一条边以后能形成一个环，那么这对婚姻就是 Unsafe 的，反之亦然。

那么，我们没有足够高的效率来删边、加边，那么应该怎么办呢？

我们考虑给无向图加方向。对于夫妻，那么就男 ( ightarrow) 女；如果是情侣，则反一下，是男 (leftarrow) 女。

然后我们跑一遍 Tarjan 强连通分量，如果夫妻在同一个强连通分量里，则如果把这条边去掉，剩下的必然能够构成匹配，即 Unsafe，反之亦然。

Code：

咕咕咕……