题外话
最初学这个算法,是在新初一的暑假里,一个初三即将毕业的学长给我们讲的。当时听得不是很懂,模板题也就只有 28pts。
后来过了好久,又想起来重新学一遍字符串,从 KMP 到 SAM 都来一遍。于是便有了这片文章。
什么是 KMP 算法
KMP 算法是由三名姓氏首字母分别为 K、M、P 的牛人发明的算法。虽然我不知道他们到底是谁hh
就像标题中那样说的,KMP 是字符串的匹配算法。
那什么叫做匹配呢?看下图就知道了:
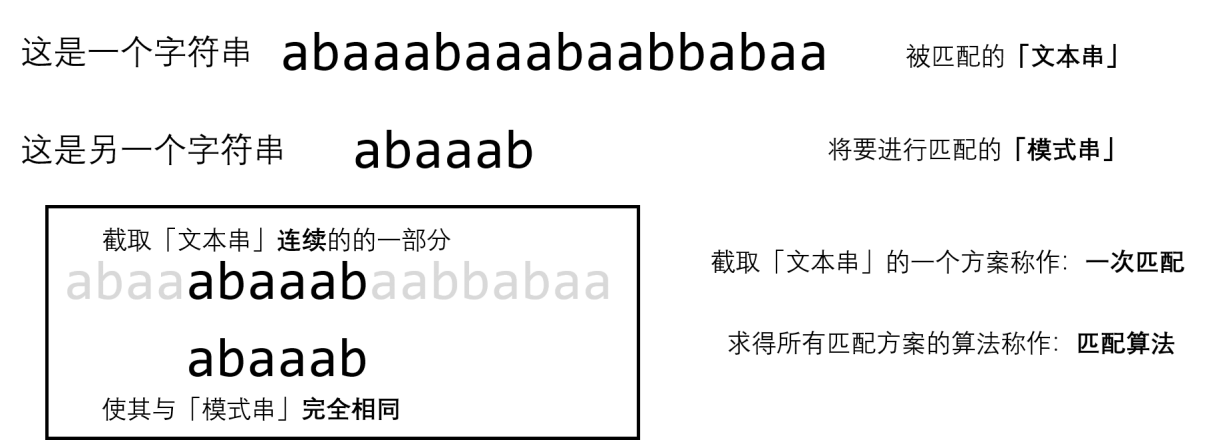
接下来,我们会大量使用此类称呼,请务必记住这几个名称!
注 1:若未特别说明,下面用 (n) 表示文本串 (S) 的长度,(m) 表示模式串 (T) 的长度。
先来一个暴力
众所周知,很多优秀的算法都由于暴力。KMP 也不例外。我们先从一个一般的暴力算法开始:
- 初始化,(i=1),(j=1);
- 开始匹配,如果 (S_i=T_j),则 (ileftarrow i+1),(jleftarrow j+1);
- 如果 (S_i eq T_j)(也称为失配),则重新令 (ileftarrow i-j+2),(jleftarrow 1);
- 特别地,如果 (j=m),即得到一次匹配,则令 (ileftarrow i-m+2),(jleftarrow 1)。
极其暴力,如果失配就从第一个没有匹配过的点开始。如果字符串是随机的可以跑得很优秀(因为很快就会失配),但是如果是精心构造过的数据就会被轻易卡到 (mathcal{O}(nm)) 从而爆炸。
优化
怎么给这种算法加上优化呢?
我们注意到,之前的失配是非常浪费时间的。如果我们能够尽量利用失配前得到的结果,是不是就能在一定程度上提高程序效率,同时保证正确性呢?
每一次匹配都为了找出可能存在的匹配方案,那么如果某些点可以在一开始就被证明是不可能存在匹配的,是不是就能节省很多时间呢?
如下图:

在 KMP 算法中,这样的前缀/后缀被称为 border(有些也称为 next 数组)。这是整个 KMP 算法优化的关键。
这样,我们就能完成匹配后的优化。那么怎么解决失配的优化问题呢?其实很简单。
失配是什么?其实是模式串的一个前缀的匹配。所以我们也可以用匹配的优化来优化失配,只是指针的边界处理略有不同而已。
经过了这样的优化,匹配的时间复杂度可以降到多少呢?注意到指向文本串的指针只增不减,而指向模式串的指针也是只增不减。每一次比较必然带来两个指针至少一个的变化,所以复杂度是 (mathcal{O}(n+m)),有了极大的优化。
这一段的 Code:(我的写法的下标从 (0) 开始)
ptr = -1;
for (int i = 0; a[i]; i++) // 指向文本串的指针
{
while (ptr != -1) // 失配时的下一步匹配
{
if (b[ptr+1] == a[i]) // 找到了下一个匹配
break;
ptr = fail[ptr]; // 这个可以暂时不用理解,接下来讲怎么计算 border 时会证明这一点
}
if (a[i] == b[ptr+1]) // 这么写而不是 (ptr == -1) 是因为最后一位也有可能匹配成功
{
ptr++; // 指针移动一位
if (ptr == lb - 1) // 发现一个匹配
{
printf("%d
", i - ptr + 1);
ptr = fail[ptr]; // 极大利用目前结果。
}
}
}
讲了这么多,我们似乎没有办法很快地求出 border,而且是模式串所有前缀的 border。我们需要引入 DP 思想。
设 (f_i) 为到第 (i) 位的前缀的 border 长度。怎么转移呢?
首先根据 border 的定义,如果 (T_{f_{i-1}+1}=T_i),也就是可以从上一位转移,即 (f_i=f_{i-1}+1)。但是如果失配了呢?
这也是 KMP 极其精髓的一点,我们要证明一个定理,从而极大地优化复杂度:
Theorem:一个 border 的 border 是原串的次大 border,即使字符串前缀和长度相等后缀一样的长度次大的方案。
一张图看懂证明(字符串用线段表示):

这个性质至关重要,也就是说我们可以通过递归的方式来依次寻找最大、次大,从而转移。
有了这个性质,之前那个用递归方式进行指针移动的思路也明白了。那么……复杂度呢?这个玄学的复杂度怎么分析呢?(我不会)总之,这里的复杂度也是线性的。
贴代码时间到:
fail[0] = -1, ptr = -1;
for (lb = 1; b[lb]; lb++) // 遍历模式串
{
while (ptr != -1) // 跳
{
if (b[ptr+1] == b[lb]) // 发现相同的
break;
ptr = fail[ptr]; // 继续跳
}
if (b[ptr+1] == b[lb]) // 理由同上
ptr++;
fail[lb] = ptr; // 数组实际上存的是指针
}
完整代码
KMP 算法的代码,可以通过模板题
#include <cstdio>
using namespace std;
const int max_n = 1000000;
char a[max_n], b[max_n];
int fail[max_n+1];
int main()
{
int ptr, lb;
scanf("%s%s", a, b);
fail[0] = -1, ptr = -1;
for (lb = 1; b[lb]; lb++)
{
while (ptr != -1)
{
if (b[ptr+1] == b[lb])
break;
ptr = fail[ptr];
}
if (b[ptr+1] == b[lb])
ptr++;
fail[lb] = ptr;
}
ptr = -1;
for (int i = 0; a[i]; i++)
{
while (ptr != -1)
{
if (b[ptr+1] == a[i])
break;
ptr = fail[ptr];
}
if (a[i] == b[ptr+1])
{
ptr++;
if (ptr == lb - 1)
{
printf("%d
", i - ptr + 1);
ptr = fail[ptr];
}
}
}
for (int i = 0; i < lb; i++)
printf("%d ", fail[i] + 1);
putchar('
');
return 0;
}