【学习笔记】二分图最大匹配 -- 从网络流到匈牙利算法

匹配，就是从图中找到一些边。使得这些边两端的点没有重复的。其中能找到最多边的就是最大匹配。

事实证明，这个东西在一般图上非常难搞，但二分图很特别，有高效解决的方法。其中最简单易懂的就是网络流和匈牙利算法。

网络流建模

显然，二分图的匹配只能是从一端的节点连向另一端。所以我们考虑如下建模：

1. 建立一个超级源点，向左端的所有点连流量为 (1) 的边；
2. 原来二分图中的边用从左端点向右端点的边代替，流量为 (1)（事实上无穷大也可以）；
3. 再建立一个超级汇点，所有右端点向其连流量为 (1) 的边。

比如：

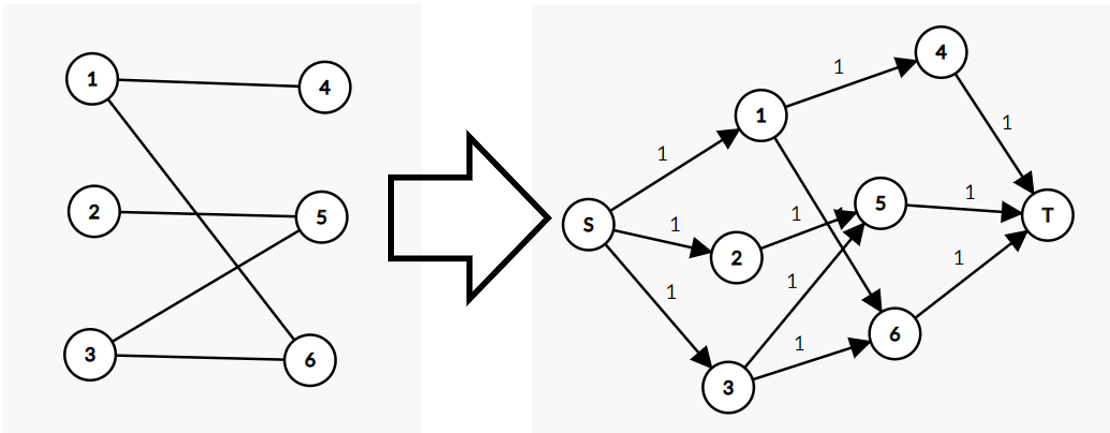
易得这样的网络流一定等于最大匹配。同时，新的边数、点数与原来的均同阶，所以复杂度与普通网络流相同。

特别地，用 Dinic 可以收获 (mathcal{O}(nsqrt{m})) 的优秀复杂度。但我不会证

匈牙利

刚刚的网络流算法固然很优秀，但是码量还是很大的。所以我们考虑一种改进。

首先我们可以得出如下结论：

引理 ( ext{I})：每一次网络流增广路贡献最多为 (1)。

这是显然的。因为边权最大只有 (1)。

引理 ( ext{II})：每个点最多只会被增广一次。

这也是显然的，根据匹配的定义可得。

引理 ( ext{III})：每一次增广路的路径必然是从没有被匹配的边开始，交错匹配的边，最后结束于没有匹配的边。

我们根据网络流增广的操作也可以得到。显然从左到右必然是未跑满流的边（也就是未匹配），而从右往左则一定是匹配过的边（否则没有反向边权）。

综上，我们考虑一种退化的网络流：每次增广也找增广路，但却是从每个节点只找一次（( ext{II})），找到交错的未匹配的边和匹配的边（( ext{III})），然后反转匹配情况。这就是匈牙利算法的整体流程。

由于各种原因，匈牙利算法的复杂度优于普通网络流。增广用 dfs 实现，则整体为 (mathcal{O}(n(n+m))sim mathcal{O}(nm))。而且——和网络流一样——基本跑不满。