预测球队比赛成绩

分析乒乓球比赛所设计出的代码：

from random import random
def printIntro():
    print("这个程序模拟两个选手A和B的某种比赛")
    print("程序运行需要A和B的能力值（0到1之间）")
def getInputs():
    a=eval(input("请输入选手A的能力值（0-1）："))
    b=eval(input("请输入选手B的能力值（0-1）："))
    n=eval(input("模拟比赛的场次："))
    return a,b,n
def simNGames(n,probA,probB):
    winsA,winsB=0,0
    for i in range(n):
        scoreA,scoreB=simOneGame(probA,probB)
        if scoreA>scoreB:
            winsA+=1
        else:
            winsB+=1
    return winsA,winsB
def gameOver(a,b):
    return a==11 or b==11
def simOneGame(probA,probB):
    scoreA,scoreB = 0,0
    serving = 'A'
    while not gameOver(scoreA,scoreB):
        if serving == 'A':
            if random()<probA:
                scoreA+=1
            else:
                serving='B'
        else:
            if random()<probB:
                scoreB+=1
            else:
                serving='A'
    return scoreA,scoreB
def printSummary(winsA,winsB):
    n=winsA+winsB
    print("竞技分析开始，共模拟{}场比赛".format(n))
    print("选手A获胜{}场比赛，占比{:.1%}".format(winsA,winsA/n))
    print("选手B获胜{}场比赛，占比{:.1%}".format(winsB,winsB/n))
def main():
    printIntro()
    probA,probB,n = getInputs()
    winsA,winsB = simNGames(n,probA,probB)
    printSummary(winsA,winsB)
main()

 根据以上的代码我们整理一下思路，这是一段通过“顶层设计”编写出来的代码，通过一些封装，我们对不同的动作进行解释

我们了解到一局乒乓球比赛的规则是，发球方发球，进行“两球制”发球，即两人固定轮流连续开两球，不论胜负，谁分数先到达11分即胜利

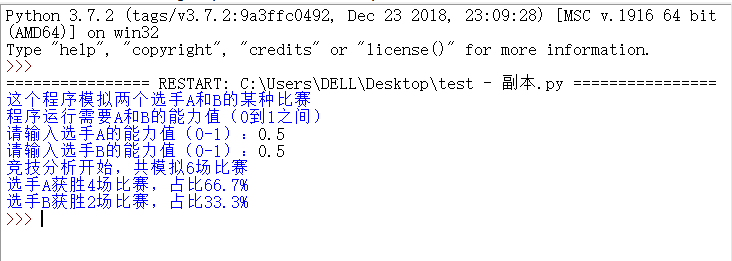
由于还有考虑最后平手时加球的情况，但上述代码暂不考虑，所以我们来看看代码的运算效果：

输入两个选手的能力值，我设置为各0.5，但结果虽较接近但还是有些许差距，排除random()的误差，我们知道这是比较符合现实的一种情况！

我们再试试能力值有细微差距的情况：

 

wow！看来仅仅只是一点点的实力差距就会有天壤之别的比赛结果……

我们再深入分析，加入更多的因素，我们知道乒乓球的赛制时单打七局四胜制，双打则是五局三胜制，所以我们先用以下代码预测单打情况：

from random import random
def printIntro():
    print("这个程序模拟两个选手A和B的某种比赛")
    print("程序运行需要A和B的能力值（0到1之间）")
def getInputs():
    a=eval(input("请输入选手A的能力值（0-1）："))
    b=eval(input("请输入选手B的能力值（0-1）："))
    return a,b
def simNGames(probA,probB):
    winsA,winsB=0,0
    for i in range(7):
        scoreA,scoreB=simOneGame(probA,probB)
        if scoreA>scoreB:
            winsA+=1
            if winsA==4:
                break
        else:
            winsB+=1
            if winsB==4:
                break
    return winsA,winsB
def gameOver(a,b):
    return a==11 or b==11
def simOneGame(probA,probB):
    scoreA,scoreB = 0,0
    serving = 'A'
    while not gameOver(scoreA,scoreB):
        if serving == 'A':
            if random()<probA:
                scoreA+=1
            else:
                serving='B'
        else:
            if random()<probB:
                scoreB+=1
            else:
                serving='A'
    return scoreA,scoreB
def printSummary(winsA,winsB):
    n=winsA+winsB
    print("竞技分析开始，共模拟{}场比赛".format(n))
    print("选手A获胜{}场比赛，占比{:.1%}".format(winsA,winsA/n))
    print("选手B获胜{}场比赛，占比{:.1%}".format(winsB,winsB/n))
def main():
    printIntro()
    probA,probB = getInputs()
    winsA,winsB = simNGames(probA,probB)
    printSummary(winsA,winsB)
main()

我们再试试结果：

我们看到，A选手最终以4-2击败B选手，即使他们能力几乎相当，也许他当下更有手感吧~

接下来是双打时，我们将刚刚的A/B选手抽象为A/B队伍，能力值为队伍的平均能力值。

from random import random
def printIntro():
    print("这个程序模拟两个选手A和B的某种比赛")
    print("程序运行需要A和B的能力值（0到1之间）")
def getInputs():
    a=eval(input("请输入选手A的能力值（0-1）："))
    b=eval(input("请输入选手B的能力值（0-1）："))
    return a,b
def simNGames(probA,probB):
    winsA,winsB=0,0
    for i in range(5):
        scoreA,scoreB=simOneGame(probA,probB)
        if scoreA>scoreB:
            winsA+=1
            if winsA==3:
                break
        else:
            winsB+=1
            if winsB==3:
                break
    return winsA,winsB
def gameOver(a,b):
    return a==11 or b==11
def simOneGame(probA,probB):
    scoreA,scoreB = 0,0
    serving = 'A'
    while not gameOver(scoreA,scoreB):
        if serving == 'A':
            if random()<probA:
                scoreA+=1
            else:
                serving='B'
        else:
            if random()<probB:
                scoreB+=1
            else:
                serving='A'
    return scoreA,scoreB
def printSummary(winsA,winsB):
    n=winsA+winsB
    print("竞技分析开始，共模拟{}场比赛".format(n))
    print("选手A获胜{}场比赛，占比{:.1%}".format(winsA,winsA/n))
    print("选手B获胜{}场比赛，占比{:.1%}".format(winsB,winsB/n))
def main():
    printIntro()
    probA,probB = getInputs()
    winsA,winsB = simNGames(probA,probB)
    printSummary(winsA,winsB)
main()

结果：A队伍以3-2赢得双打比赛~

接下来我们分析篮球赛事，我们知道篮球是一项团队的运动，所以左右比赛的走向的的变量更加多首先是运动员的人数较多，场上每一队应该有5名队员在场，场下有4-5名替补队员，这样加起来双方队伍参赛队员将在14-20个，同时能力值有不同，且若精确到每一次进攻，那么就会有进攻成功及进攻失败，或进攻一次伴随着抢板之后再次补篮等多种复杂情况……由于现实的多变性，考虑到本次只是简单的模拟，我对现实进行理想化，只讨论场上每队主力5名队员的能力值，并通过各值推出该队平均能力值，由于篮球比赛以时间作为指标，在指定时间内获得分数最高者胜，所以我们将其简化为：在一定时间内，只能有有限次的进攻次数，根据现实情况，我们设置为：200次（双方进攻总数），于是有了下面的代码：

from random import random
import time as T

def printIntro():
    print("这个程序模拟两支球队A和B的篮球比赛")
    print("程序运行需要A队和B队的能力值（0到1之间）")
def getInputs():
    print("现在请分别输入A队中上场的五位球员的能力值")
    a=eval(input("请输入选手1的能力值（0-1）："))
    b=eval(input("请输入选手2的能力值（0-1）："))
    c=eval(input("请输入选手3的能力值（0-1）："))
    d=eval(input("请输入选手4的能力值（0-1）："))
    e=eval(input("请输入选手5的能力值（0-1）："))
    print("现在请分别输入B队中上场的五位球员的能力值")
    f=eval(input("请输入选手6的能力值（0-1）："))
    g=eval(input("请输入选手7的能力值（0-1）："))
    h=eval(input("请输入选手8的能力值（0-1）："))
    i=eval(input("请输入选手9的能力值（0-1）："))
    j=eval(input("请输入选手10的能力值（0-1）："))
    meanA=(a+b+c+d+e)/5
    meanB=(f+g+h+i+j)/5
    print("A队的平均能力值为{0}，B队的平均能力值为{1}".format(meanA,meanB))
    return meanA,meanB
def simOneAttack(probA,probB,):
    scoreA,scoreB = 0,0
    serving = 'A'
    for i in range(200):
        if serving == 'A':
            if random()<probA:
                scoreA+=2
            else:
                serving='B'
        else:
            if random()<probB:
                scoreB+=2
            else:
                serving='A'
    print("最终A队得分为{0}，B队为{1}".format(scoreA,scoreB))
    print("队伍A获胜概率为{:.1%}".format(scoreA/200))
    print("队伍B获胜概率为{:.1%}".format(scoreB/200))
    print("平手概率（不加时）：{:.1%}".format(1-(scoreA/200)-(scoreB/200)))
    return scoreA,scoreB 
def main():
    printIntro()
    probA,probB = getInputs()
    print("竞技分析开始，共模拟200次进攻")

    simOneAttack(probA,probB)
main()

结果如下图：

分别输入各个队伍主力球员的能力值，求出各队伍平均能力值，并最终预测比赛得分为：A:B=86:110

这是我们预测了一次比赛的结果。

我们继续分析，在NBA的规则中，需要先在本土30支队伍中通过进行82场常规赛决出8强，于是我们对其进行变体来预测A/B两支队伍进行多场比赛后的结果：

from random import random
import time as T

def printIntro():
    print("这个程序模拟两支球队A和B的篮球比赛")
    print("程序运行需要A队和B队的能力值（0到1之间）")
def getInputs():
    print("现在请分别输入A队中上场的五位球员的能力值")
    a=eval(input("请输入选手1的能力值（0-1）："))
    b=eval(input("请输入选手2的能力值（0-1）："))
    c=eval(input("请输入选手3的能力值（0-1）："))
    d=eval(input("请输入选手4的能力值（0-1）："))
    e=eval(input("请输入选手5的能力值（0-1）："))
    print("现在请分别输入B队中上场的五位球员的能力值")
    f=eval(input("请输入选手6的能力值（0-1）："))
    g=eval(input("请输入选手7的能力值（0-1）："))
    h=eval(input("请输入选手8的能力值（0-1）："))
    i=eval(input("请输入选手9的能力值（0-1）："))
    j=eval(input("请输入选手10的能力值（0-1）："))
    meanA=(a+b+c+d+e)/5
    meanB=(f+g+h+i+j)/5
    print("A队的平均能力值为{0}，B队的平均能力值为{1}".format(meanA,meanB))
    return meanA,meanB
def simNGames(probA,probB):
    winsA,winsB=0,0
    for i in range(82):
        scoreA,scoreB=simOneAttack(probA,probB)
        if scoreA>scoreB:
            winsA+=1
        else:
            winsB+=1
    print("最终A队得分为{0}，B队为{1}".format(scoreA,scoreB))
    return winsA,winsB
def simOneAttack(probA,probB,):
    scoreA,scoreB = 0,0
    serving = 'A'
    for i in range(200):
        if serving == 'A':
            if random()<probA:
                scoreA+=2
            else:
                serving='B'
        else:
            if random()<probB:
                scoreB+=2
            else:
                serving='A'

    return scoreA,scoreB
def printSummary(winsA,winsB):
    n=winsA+winsB
    print("竞技分析开始，共模拟{}场比赛".format(82))
    print("队伍A获胜{}场比赛，占比{:.1%}".format(winsA,winsA/n))
    print("队伍B获胜{}场比赛，占比{:.1%}".format(winsB,winsB/n))
def main():
    printIntro()
    probA,probB = getInputs()
    print("竞技分析开始，共模拟200次进攻")
    simOneAttack(probA,probB)
    winsA,winsB = simNGames(probA,probB)
    printSummary(winsA,winsB)
main()

结果：