在上一篇文章里面,我们提到了解线性动态模型的四种代表性方法,并画了这么一张图来表示他们之间的关系。这一篇文章中,我就针对他们的原理以及相互关系,来进行一些介绍。
考虑到这四种方法中,朴素贝叶斯,隐马尔可夫,最大熵模型都是比较熟悉的,所以不做重点介绍,介绍的中心会放在中文资料很少的CRF(中文有人翻译成条件随机场)上面。但CRF会由以上三种方法引出来。
好,切入正题。先给出演示情景模型。假设我们有特征向量x=(x1,x2,……xm),你可以把它们想像成一封封即将来到你邮箱的邮件,现在你想对 这些邮件进行判断归类,这个类别变量就是y,把y看成是向量集的话,就是y=(y1,y2,……,ym)。 我们先从最简单的Naive Bayes入手分析这个模型吧。根据概率知识我们知道,
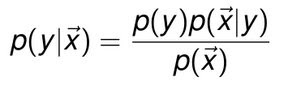
把p(x)作为已知量
![]()
再假设所有xi条件独立
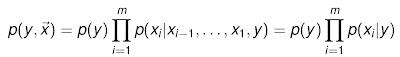
这就是简单得不可思议的朴素贝叶斯。如果用一个示意图而不是公式来表示的话,朴素贝叶斯等同于这样一个模型
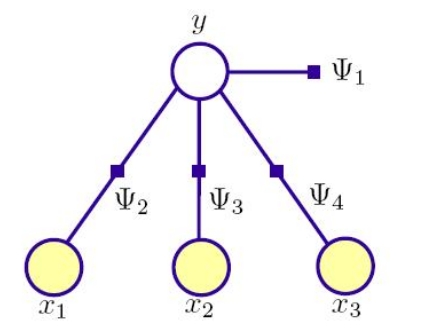
你看,连模型都简单清晰。
注:关于图中出现的factor graph和Psi函数的意义,动态模型及其求解介绍—下文中将有涉及。这里就简单看成条件概率分布示意图也不妨碍理解。
关于为什么朴素贝叶斯效果这么好,Pongba曾经在其一堆长文中的一篇中写过
有人对此提出了一个理论解释,并且建立了什么时候朴素贝叶斯的效果能够等价于非朴素贝叶斯的充要条件,这个解释的核心就 是:有些独立假设在各个分类之间的分布都是均匀的所以对于似然的相对大小不产生影响;即便不是如此,也有很大的可能性各个独立假设所产生的消极影响或积极 影响互相抵消,最终导致结果受到的影响不大。具体的数学公式请参考这篇 paper 。
贝叶斯在其他领域中也有很好的应用效果,以后有时间我可以结合我上一篇论文的内容来展开谈一谈。
好,介绍完贝叶斯,我们介绍一下隐马尔可夫模型。我们从文章开始的图中可以看到,NB加一个sequence的特性,就成了HMM,是怎么回事呢? 其实,HMM就可以当作NB的序列扩展。我们刚才看到,在贝叶斯系统中,状态变量是和观察量相关的,但状态之间没有关系。但如果我们需要处理的系统,状态 和状态之前也有概率分布呢?这就等于是一个由很多朴素贝叶斯组合成的一个大网络。而HMM,正好就是贝叶斯网络的特例。其表示方式和NB大同小异,只是现 在需要将状态变量之间的依赖体现进来,可以得到
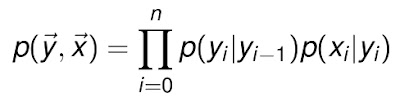
而代表HMM的示意图则是NB示意图的变种
从NB和HMM的分析,可以看到,两者关注的都是特征向量和状态向量的联合概率密度,因此,从上一篇文章的介绍中可以得知,他们是典型的generative model。
然后我们再介绍一下discriminative模型的两个代表。首先是最大熵算法模型,下面统称ME。说起熵,这东西真是从本科跟我到现在,阴魂不散啊。曾经参与过TopLanguage关于熵的讨论, 对于熵还不是很清楚的童鞋,可以去围观一下。Xuyou对于熵的数学解释是很完备的,只是对于熵本身来说,已经被用来作为物理,数学,通信等系统不确定性 的统一表现了,而既然熵是用概率表示的,所以通常依赖于观察者,一个人对系统可能有与他人不同的认识,所以也就会有对熵不同的计算理解。
ME算法的中心思想是,如果概率分布信息不确定,那么最不会产生偏置的做法,就是均等看待概率分布,不要做任何主观假设。于是在给定关于训练数据的限制条件(例如特征函数的期望值等于观测值)下,让模型的熵最大的那个分布,就是所求分布。
不知道这样说是不是有点绕,如果觉得这个大概念有点难理解,可以看看吴军数学之美系列中讲解最大熵意义的文章,大家都知道,出于水平原因,我是不可能讲得比他还好的:)。
日常生活中,很多事情的发生表现出一定的随机性,试验的结果往往是不确定的,而且也不知道这个随机现象所服从的概率分布, 所有的只有一些试验样本或样本特征,于是在这种情况下,如何对分布作出一个合理的推断就成了需要研究的问题。最大熵采取的原则就是:保留全部的不确定性, 将风险降到最小。在金融理论中,一个类似的教训是,为了降低风险,投资应该多样化,不要把所有的鸡蛋都放在一个篮子里。
最大熵模型的建立是很复杂的,计算量也非常大,吴军的文章没有仔细讲详细的模型建立方程。这里我也只是粗略提一下。假设x是一个人的性别,y表示名字
比如对于p(y|x)来讲,条件熵是
![]()
所以,我们要找的目标函数是
![]()
我们手头有什么样的特征变量呢?我们有x,已知的上下文信息,我们有y,需要确定的信息。如果说yi是y的一个实例,xi就是yi的上下文。我们的特征函数是
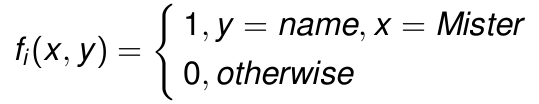
好,这样就可以得到特征函数的数学期望了。这里的p(x,y),表征的是(x,y)在样本中出现的联合概率。也就是说,这个数学期望值,是f关于p(x,y)经验分布的期望值。
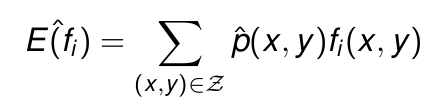
而当我们把p(x,y)写成另一种形式的时候,发现如果把特征单独拿出来放在实际中考虑时,能得到期望值的另外一种形式,也就是单独对p(x)求一次期望值。这时候整个f的期望值是:
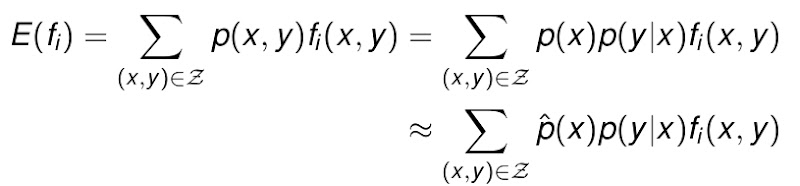
好,有了期望值和观察值,那么我们就可以定义什么是consistent的ME模型了。只要满足![]() 条件,我们就说这是一个consistent的ME模型。
条件,我们就说这是一个consistent的ME模型。
上面的这个条件是最大熵模型约束条件中的一个,所谓约束条件,就是说,你要用这个模型,你的系统就必须满足约束条件。总结来说,一个最大熵模型需要的约束条件如下:
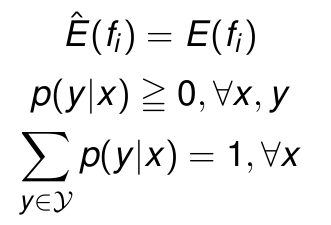
注意,第一点刚才已经提到,其物理意义是,我们知道某个量的期望值,这个量是系统每个状态都有的量,期望值可以这样求出:考虑那些状态的概率,对每个状态响应的值求平均值。所以如果对于量 G 每个状态都有一个值,期望值就是G的概率分布。正好对应刚才我们的公式。
第二点显然,那第三点代表什么意思呢?就是说,你这个系统,可以有多个可能的状态,每个状态对应一个概率,但输入事件必须是互斥而完备的,所以这些概率和必须是1。正是因为多个概率带来的不确定性,我们才会用熵的方式去建模。
这三个约束是很重要的,很多时候,可以直接从约束公式来求解问题。
看到这里,我们会发现,这其实是一个约束优化的问题,我们有线性的条件等式,但目标函数是非线性的,属于线性约束下的非线性规划问题。这个问题的等价命题是,如何求的下列方程的最大值,来获得y条件于x的概率。
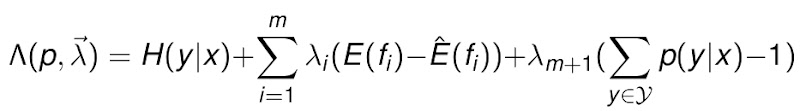
这个问题,解决的思路通常是,用拉格朗日乘子将带约束的非线性规划转为不带约束的非线性规划,然后用偏导数法求解该问题,最后解方程。这个过程过于繁杂,这里就不赘述了,感兴趣的同学请围观这篇文章。总之最后的建模是
还是和其他方法一样,用一个示意图来表示ME
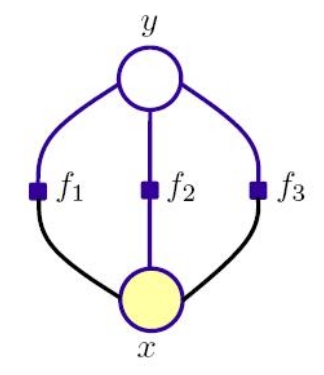
从示意图上看,ME和Bayes结构上有一些类似,但实际上两者是有很大区别的。区别主要体现在:
1 Bayes对输入的确定程度要求高,它只有在程序无损失(输入可以被准确认定)或者假定了输入概率分布的情况下才适用。而ME是一个更一般的方法,它可以 用于估计输入概率。结果是一个与已知约束一致的概率分布,约束用一个以上的量的平均值,或期望值描述,但是又尽可能的没有偏差。
2 从限制程度看,约束条件让ME受更多限制,应用不如NB广。从ME的原理来看,主要用于classification,但用于做prediction不合适。因为在ME里,状态的确定仅依赖于当前的观测,可能出现前后状态标注不一致的情况。
3 关于ME和NB的区别和联系,学术界本身都还在讨论,也没有一个定论。
聪明的你在看到“前后标注不一致”时,肯定会想到,马尔可夫不就是解决这个问题的么?对,把最大熵和马尔可夫结合起来,引入状态前后的概率,就是所 谓的最大熵马尔可夫模型。这个模型很好,因为首先解决了最大熵标注不一致的问题,其次,在讲马尔可夫的时候我们提到,其对特征独立的要求很严格。但结合最 大熵后,我们发现,这个模型的当前状态,只依赖于前一状态和当前观察,标注不一致没了,也不要求特征的独立性了,非常灵活。
那么最大熵马尔可夫模型有没有缺点呢?当然有,马尔可夫一直有的label bias,中文叫标注偏置的缺点,也被它继承了。要克服这个问题,就涉及到我要说的最后一种方法,条件随机场,该方法将在动态模型及其求解介绍—下文中介绍。
××××××××××××××××××××××××××××××
系列链接: