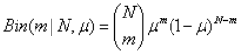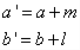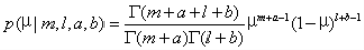1）Likelihood
最大似然估计提供了一种给定观察数据来评估模型参数的方法，即：“模型已定，参数未知”。
简单而言，假设我们要统计全国人口的身高，首先假设这个身高服从
服从正态分布，但是该分布的均值与方差未知。我们没有人力与物力去统计全国每个人的身高，但是可以通过采样，获取部分人的身高，然后通过最大似然估计来获
取上述假设中的正态分布的均值与方差。
最大似然估计中采样需满足一个很重要的假设，就是所有的采样都是独立同分布的。
下面我们具体描述一下最大似然估计：
首先，假设
为独立同分布的采样，θ为模型参数,f为我们所使用的模型，遵循我们上述的独立同分布假设。参数为θ的模型f产生上述采样可表示为
回到上面的“模型已定，参数未知”的说法，此时，我们已知的为
，未知为θ，故似然定义为:
在实际应用中常用的是两边取对数，得到公式如下：
其中
称为对数似然，而
称为平均对数似然。而我们平时所称的最大似然为最大的对数平均似然，即：
由上可知最大似然估计的一般求解过程：
（1） 写出似然函数；
（2） 对似然函数取对数，并整理；
（3） 求导数 ；
（4） 解似然方程
Likelihood函数选择
对于 同一个模型，likelihood函数可能有不同的选择，对于这些选择，可能有些比较精确、但是会搜索非常大的空间，可能有些比较粗糙，但是速度会比较 快，我们需要选择不同的likelihood函数来计算后验概率。对于这些Likelihood函数，可能还需要加上一些平滑等技巧来使得最大的降低数据 中噪声、或者假设的缺陷对结果的影响。
我所理解的用贝叶斯的方法来估计给定数据的假设的后验概率，就是通过prior * likelihood，变换到后验分布。是一个分布变换的过程。
3) loss function(损失函数)
x是输入的数据，y(x)是推测出的结果的模型，t是x对应的真实结果，L(t,y(x))就是loss function，E[L]表示使用模型y进行预测，使用L作为损失函数的情况下，模型的损失时多少。通常来说，衡量一个模型是否能够准确的得到结果，损 失函数是最有效的一个办法，最常用、最简单的一种损失函数是：
不过我一直不知道为什么这里用的平方，而不是直接用绝对值，有详细一点的解释吗？:-p
4) Model Selection(模型选择)
前 文说到了对于likelihood函数可以有不同的选择，对于先验的概率也可以有不同的选择，不过假设我们一个构造完整的测试集和一个恰当的损失函数，最 终的结果将会是确定的，量化的，我们很容易得到两个不同参数、方法的模型的优劣性。不过通常情况下，我们的测试集是不够完整，我们的损失函数也是不那么 的精确，所以对于在这个测试集上表现得非常完美的模型，我们常常可能还需要打一个问号，是否是训练集和测试集过于相像，模型又过于复杂。导致了over- fitting（后文将会详细介绍over-fitting的产生）？
Model Selection本质上来说是对模型的复杂度与模型的准确性做一个平衡，本文后面将有一些类似的例子。
Example 1：Sequential 概率估计
注：此例子来自PRML chapter 2.1.1
对于概率密度的估计，有很多的方法，其中一种方法叫做Sequential 概率估计。
这种方法是一个增量的学习过程，在每看到一个样本的时候都是把之前观测的数据作为先验概率，然后在得到新数据的后验概率后，再把当前的后验概率作为下一次预测时候的先验概率。
传统的二项式分布是：
由于传统的二项式分布的概率μ是完全根据先验概率而得到的，而这个先验分布之前也提到过，可能会由于实验次数不够而有很大的偏差，而且，我们无法得知μ的分布，只知道一个μ的期望，这样对于某些机器学习的方法是不利的。为了减少先验分布对μ的影响，获取μ的分布，我们加入了两个参数，a，b，表示X=0与X=1的出现的次数，这个取值将会改变μ的分布，beta分布的公式如下：
对于不同a，b的取值，将会对μ的概率密度函数产生下面的影响：（图片来自PRML）
在观测数据的过程中，我们可以随时的利用观测数据的结果，改变当前μ的先验分布。我们可以将Beta分布加入两个参数，m，l，表示观测到的X=0，X=1的次数。（之前的a，b是一个先验的次数，不是当前观测到的）
我们令：
a’，b’表示加入了观测结果的新的a，b 。带入原式，可以得到
我们可以利用观测后的μ后验概率更新μ的先验概率，以进行下一次的观测，这样对不时能够得到新的数据，并且需要real-time给出结果的情况下很有用。不过Sequential方法有对数据一个i.i.d（独立同分布）的假设。要求每次处理的数据都是独立同分布的。
原文 http://www.cnblogs.com/LeftNotEasy/archive/2010/09/27/1837163.html