对于组合数我们可以将其表示成阶乘的形式:C(n,k)= 。那我们不妨把这三个阶乘全部表示成上个专题的形式。这样的话,如果对于e1>e2+e3就可以被p整除,e1=e2+e3就无法被p整除。在无法被整除的情况下C(n,k)=a1(a2a3)-1

1 int mod_comb (int n, int k, int p){ 2 if (n<0||k<0||n<k) return 0; 3 int a1=mod_fact(n,p,e1),a2=mod_fact(k,p,e2),a3=mod_fact(n-k,p,e3); 4 if (e1>e2+e3)return 0; 5 return a1*mod_inverse(a2*a3%p, p) %p; 6 }
另外,我们也可以用Lucas来求。
Lucas定理:我们令n=sp+q , m=tp+r(q,r ≤p)则有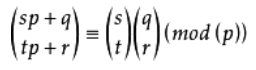
具体证明如下:
首先我们先来证明一个简单的算式: (f!=p&&f!=0)
(f!=p&&f!=0)
C(p , f)%p= p!/(f!(p-f)!)%p因为p是素数,并且分母上的f和(p-f)都要比p要小,也就是说在分母上没有数可以把p约去,所以C(p,f) %p一定等于0。
证明完了这个算式,我们就可以开始证明卢卡斯定理。
对于(1+x)sp+q≡(1+x)sp×(1+x)q≡((1+x)p)s×(1+x)q≡(根据二项式定理展开,然后在有上面的公式,所以我们可以得到)(1+xp)s×(1+x)q≡(再根据二项式定理展开)≡  (mod p)
(mod p)
最终我们可以得到
下面我们来计算一下左右两边xtp+r的系数:
左边=C(sp+q ,tp+r);右边=C(s ,t)×C(q, r)
因为左边=右边,所以我们最后得到了卢卡斯定理。
有了卢卡斯定理,我们就有了这样的代码,这个代码真的很好理解

1 int Lucas(int n,int m,int p){ 2 long long ans=1; 3 while(n&&m&&ans){ 4 ans*=comb(n%p,m%p,p)%p;//comb()求组合数 5 n/=p;m/=p; 6 } 7 return ans; 8 }
