线性回归简析
我理解的线性回归就是,比较简单的一维的线性回归,所要求解的方程就是y=wx+b
你要做的就是不断的学习数据集,不断的更新w和b,让损失函数越小越好。
损失函数便是你程序求得的结果和标准结果之间的误差,损失函数具体公式如下:
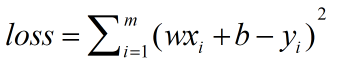
w值梯度下降公式:w'=w-学习速率*斜率
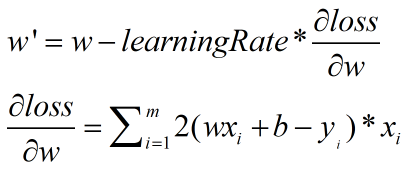
b值梯度下降公式:b'=b-学习速率*斜率
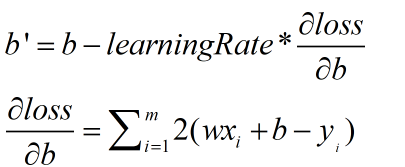
绘制的数据集图像:

# 线性回归:y=0.3x+0.7
import numpy as np
import matplotlib.pyplot as plt
import time
# 损失函数
def data_loss(w, b, dataSet):
loss = 0
for i in range(len(dataSet)):
x = dataSet[i][0]
y = dataSet[i][1]
loss += (w * x + b - y) ** 2
loss /= float(len(dataSet))
return loss
# 更新w和b
def update_w_b(w, b, learningRate, dataSet):
wSlope = 0.0
bSlope = 0.0
for i in range(len(dataSet)):
xi = dataSet[i][0]
yi = dataSet[i][1]
# 计算w和b的斜率
wSlope += 2 * (w * xi + b - yi) * xi / float(len(dataSet))
bSlope += 2 * (w * xi + b - yi) / float(len(dataSet))
# 计算学习过一边之后的w,b,并返回,,具体推导公式看代码区上边
w1=w-learningRate*wSlope
b1=b-learningRate*bSlope
# 返回更新后的w和b
return [w1,b1]
def run_study(learningRate, dataSet, studyNum, w, b):
w1=w
b1=b
for i in range(studyNum):
# 传参一定要注意,要传w1,b1,这样才能学习
w1, b1 = update_w_b(w1, b1, learningRate, dataSet)
print("--------------------------------------")
print("Study {0}:
w={1}
b={2}
data_loss={3}"
.format(i + 1, w1, b1, data_loss(w1, b1, dataSet)))
if __name__ == '__main__':
# 定义一个计时器
tic=time.time()
# 学习速率
learningRate = 0.002
# 学习次数
studyNum = 2000
# 数据集
dataSet = []
# 构造线性方程
for i in range(studyNum):
x = np.random.normal(0.0, 1)
# 要学习的线性方程:y=0.3x+0.7
y = 0.3 * x + 0.7 + np.random.normal(0, 0.03)
dataSet.append([x, y])
# 打印一下看看数据集效果
xData = [i[0] for i in dataSet]
yData = [i[1] for i in dataSet]
plt.scatter(xData, yData)
plt.show()
# 开始学习
run_study(learningRate, dataSet,studyNum, 0, 0)
# 记录学习用时
toc=time.time()
print("Time : "+str(1000*(toc-tic))+"ms")
# 最终结果:
# Study 2000:
# w=0.29921579295614104
# b=0.699757591874389
# data_loss=2.8178229011593263e-07
# Time : 5248.762607574463ms