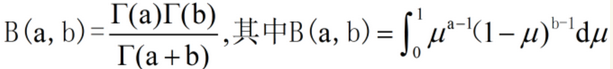计算beta分布并画图（1）

贝塔函数与伽马函数的关系


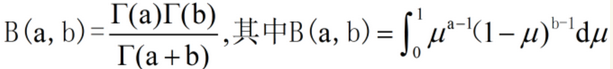
详细推导过程见LDA漫游指南
java的org.apache.commons.math3.special.Gamma封装了Gamma函数可以直接使用
本文首先计算出B(3.9,2.9)与B(3.9,5.3)的100个散点，然后绘制出Beta分布图像

import java.io.BufferedWriter;
import java.io.FileWriter;
import java.io.IOException;
import org.apache.commons.math3.special.Gamma;

public class betadistr {
                
        public static double Gammafun(double alpha){        
            return Gamma.gamma(alpha);                
         }
         public static double Bfunction(double alpha,double beta) {
            double totgamm = Gammafun(alpha+beta);
            double addgamm = Gammafun(alpha)*Gammafun(beta);
            return addgamm/totgamm;
        }
         public static void valued() throws IOException {
            
            BufferedWriter writer = new BufferedWriter(new FileWriter(filename));            
            int K=2;
            double[][] m=new double[K][100];            
            double b[][]= new double[2][2];
            b[0][0]= 3.9;
            b[0][1]= 2.9;
            b[1][0]= 3.9;
            b[1][1]= 5.3;
                                                                           
            for (int i = 0; i < K; i++) {            
                    for (int x = 0; x < 100; x++) {
                        double y = (double)x/100;            
                        double f=Math.pow(y,b[i][0]-1)*Math.pow(1-y, b[i][1]-1);                        
                        double z=Bfunction(b[i][0],b[i][1]);
                        m[i][x]=f/z;
                        writer.write(m[i][x] + "	");
                        System.out.println(m[i][x]);
                   }
                writer.write("
");
               }                            
              
            writer.close();  
                                        
        }
         
                 
        
         public static void main(String[] args) throws IOException {
            valued();
            
         }
    }