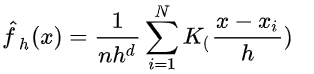核密度估计
密度函数就是分布函数的一阶导数
对现有数据来估计密度函数的时候,可以用分布函数的一阶导数进行估计。
找离散数据的分布函数可以用(小于t的样本数)/(总样本数),但这个是不可导的,没办法找导数
这时候考虑导数的定义
![]()
就是看在(-h, h)区间有多少个样本点,那么密度函数的估计就变成:
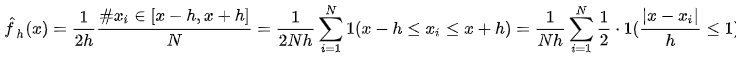
(h怎么选取?最优的h应该是N的-1/5次方乘以一个常数,也就是 ![]() )
)
之后我们定义一个函数K,且这个K函数的积分保证等于1,那么就可以将密度函数的估计变成
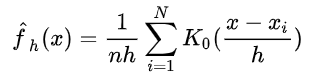
这里的K可以用很多函数表示,只要保证他的积分是1就行,比如我们可以用标准正态密度函数作为K
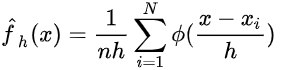
扩展到多维的情况,就有:(d是维度,K是多维的kernel,h一般称为窗宽。)