一,高级语言和机器指令中的运算
1,C程序中涉及的运算
①按位运算
符号|表示按位OR运算;符号&表示按位AND运算;符号~表示按位NOT;符号^表示按位XOR运算。
②逻辑运算
符号||表示OR运算;符号&&表示AND运算;符号!表示NOT运算。
③移位运算
逻辑移位:不考虑符号位,把高(低)位移出,低(高)补0。 对于无符号整数的逻辑左移,如果最高位移出的是1,则发生溢出。
算术移位:对于带符号位整数的移位操作。左移时,高位移出,低位补0,每移一位,如果移出的高位不同于移位后的符号位,即左移前,后符号位不同,则发生溢出;左移时,低位移出,高位补符号。
④位扩展和位截断运算
0扩展用于无符号数,只要在短的无符号数前面添加足够的0即可。
符号扩展用于补码表示的带符号整数。通过在短的带符号整数前添加足够多的符号位来扩展。
2,MIPS指令中涉及的运算
高级语言中的所有运算都是通过指令系统中的运算指令实现的。利用MIPS提供的运算指令完全能够实现C语言所需求的各种运算要求。
二,基本运算部件
用一个专门的算术逻辑部件(ALU)来完成基本逻辑运算和定点数加减运算,各类定点乘除运算和浮点数运算则可利用加法器或ALU和移位器来实现,因此基本的运算部件是加法器,ALU和移位器,ALU的核心部件是加法器。
1.串行进位加法器
全加器用来实现两个本位数加上底位进行生成一位本位以及一位向高位的进位,第i位的加法运算是指第i位加数Xi,Yi,和低位的进位Ci-1三者相加,得到本位和Fi的第i位的进位输出Ci。
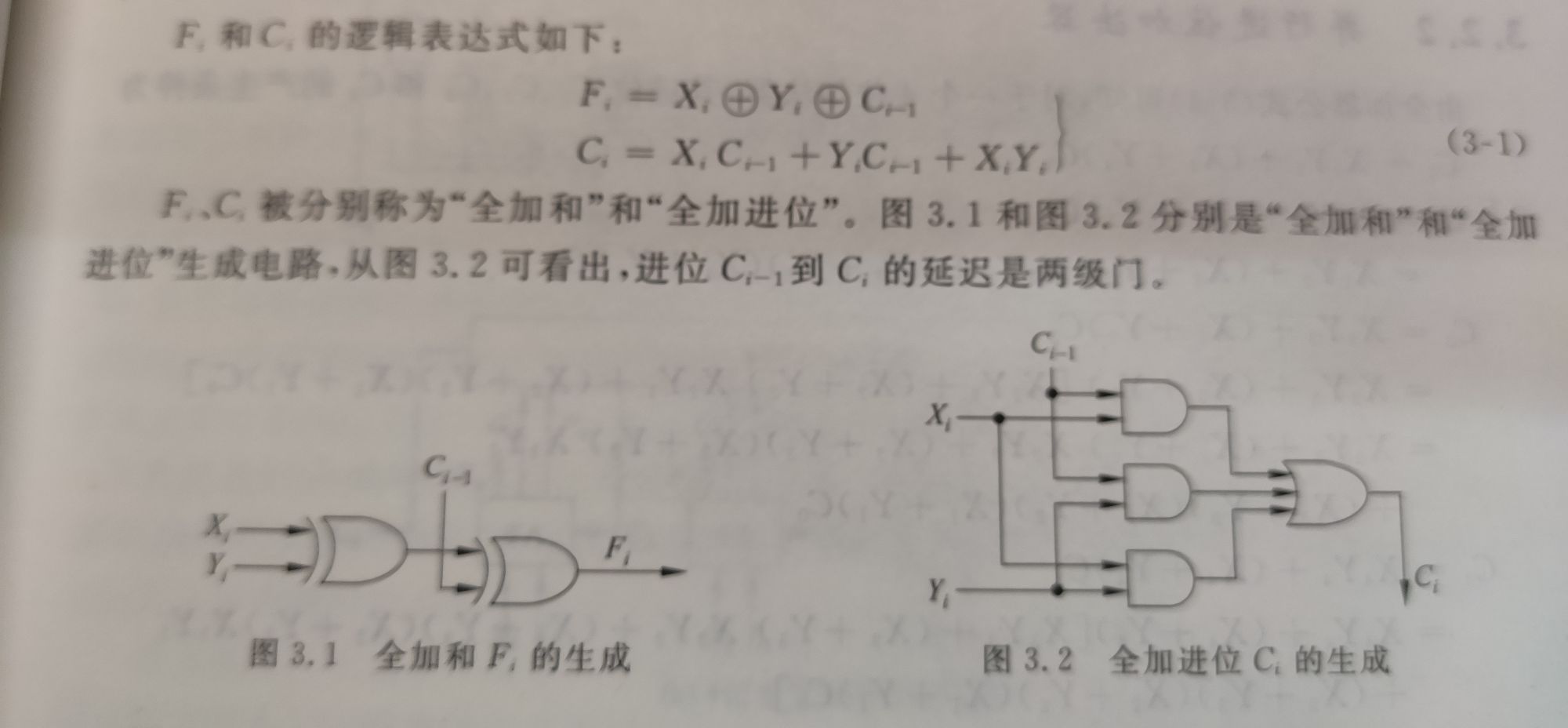
2.并行进位加法器
用n位全加器实现两个n位操作数各位同时相加,这种加法器称为并行加法器。并行加法器中全加器的个数与操作数的位数相同。并行加法器中全加器的位数与操作数的位数相同,可同时对操作数的各位相加

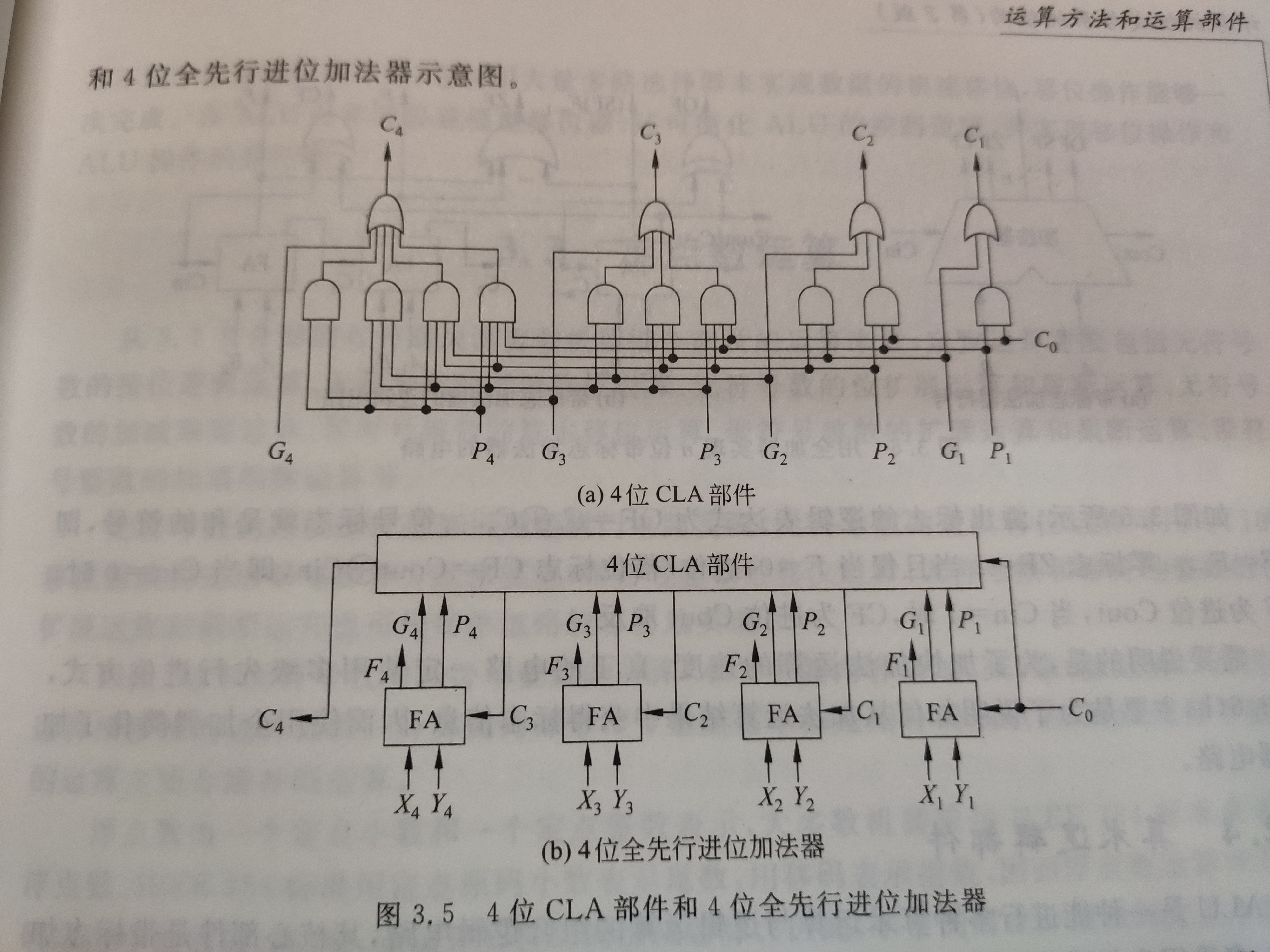
3.带标志加法器
n位无符号数加法器只能用于两个n位二进制数相加,不能进行无符号整数的减运算,也不能进行带符号整数的加/减运算。要能够进行无符号整数的加/减运算和带符号整数的
加/减运算,还需要在无符号数加法器的基础上增加相应的逻辑门电路,使得加法器不仅能计算和/差,还要能够生成相应的标志信息。
4.算术逻辑部件
ALU是一种能进行多种算术运算与逻辑运算的组合逻辑电路,其核心部件是带标志加法器,多采用先行进位方式。
三,定点数运算
1.补码加减运算
若两个补码表示的n位定点整数[X]补=Xn-1Xn-2…X0,[y]补=Yn-1Yn-2…Y0。
表达式:
[x+y]补=[x]补+[y]补(mod2^n)
[x-y]补=[x]补+[-y]补(mod2^n)
2.原码加减运算
原码加减运算运算规则:
(1)比较两个操作数的符号,对加法实行“同号求和,异号求差”,对减法实行“异号求和,同号求差”。
(2)求和时,数值位相加,若最高位产生进位则结果溢出。和的符号位取被加数(或被减数)的符号。
(3)求差时,被加数(或被减数)数值位加上加数(或减数)数值位的补码,并按以下规则产生结果
①最高数值位产生进位,表明加法结果为正,所得数值位正确
②最高数值位没有产生进位,表明加法结果为负,得到的是数值位的补码形式,因此需要对结果求补,还原为绝对值形式的数值位
③在上述(1)的情况下,差的符号位取被加数(被减数)的符号;在上述(2)d的情况下,符号位为被加数(被减数)的符号取反
3.移码加减运算


4.原码乘法运算
①原码一位乘法
②原码二位乘法
5.补码乘法运算
①补码一位乘法
将符号与数值位合在一起参与运算,直接得出用补码表示的乘积,且正数和负数同等对待。
②补码二位乘法
两位一乘,,把乘数分为两位一组,根据两位代码的组合决定加或减被乘数的倍数,形成的部分积每次右移两位。
6.快速乘法器
- 列阵乘法器
7.原码除法运算
1.恢复余数除法
(1)对于无符号整数除法来说,如果被除数为2n位,则商有可能会超出n位无符号整数范围,所以,若Q.1,则发生溢出。
留最高位的商Qn=1,继续执行下去。
(2)对于原码定点小数除法来说,若Q=1,则相除结果的数值从小数部分溢出到了整数部分,按道理,两个定点小数相除,结果也应是定点小数,故应当作溢出处理。但浮点数尾数溢出时,可通过右规来消除,最终只要阶码不溢出,结果仍然正确。所以,这种情况下,保留最高位的商Qn=1,继续执行下去。
第2步:若已求得第主次的中间余数为Ri,,则第i+1次的中间余数为Ri+1=2Ri-Y。若Ri+1<0,则上商Qn-i=0,同时恢复余数,即Ri+1=Ri+1+Y;若Ri+1>=0,则上商Qn-i=1。
第3步:循环执行第2步n次,直到求出所有n位商Q1~Q0为止。
最终,商在Q寄存器中,余数在R寄存器中。
2.不恢复余数除法
在恢复余数除法中,第i次余数为Ri=2Ri-Y。根据下次中间余数的计算方法,有以下两种不同情况:
(1)若Ri≥0,则上商1,不需恢复余数,直接左移一位后试商,得下次余数Ri+1,即Ri+1-Y。
(2)若R<0,则上商0,且需恢复余数后左移一位再试商,得下次余数Ri+1,即R+1=2(Ri+Y)-Y=2Ri+Y。
8.补码除法运算
1.补码恢复余数除法
根据补码除法判断是否够减的判断规则,可以得到如下补码恢复余数除法的算法要点
(1)操作数的预置:除数装人除数寄存器Y,被除数符号扩展后装入余数寄存器R和余数/商寄存器Q.
(2)R和Q同步串行左移一位。
(3)若R与Y同号,则做减法,即R=R-Y;否则,做加法,即R=R十Y,并按以下规则确定第i次循环得到的商Qn—i。
①若R和Q中的余数=0或R操作前后符号未变,则表示够减Qn-i置1,转第(4)步
②若R操作前后符号已变,表示不够减,则Qn-i置0,恢复R值后转第(4)步。
(4)重复第(2)步和第(3)步,直到取得n位商为止。
(5)若被除数与除数同号,则Q中是真正的商;否则,将Q中的数值求补。
(6)余数在R中
从上述算法要点可以看出,在进行置商时,采用了“够减则上商为1,不够减则上商为1,不够减则上商为0”的上商方式,因此,最后若商为负值,则需要‘各位取反,末位加1”来得到真正的商。
2.补码不恢复余数除法

四、浮点数运算
1.浮点数加减运算
- 对阶:使x,y的阶码相等,以使尾数可以相加减。
- 原则:小阶向大阶看齐,阶小的那个数的尾数右移,右移的位数等于两个阶(指数)的差的绝对值。
- 尾数加减:对阶后两个浮点数的指数相等,此时,可以进行对阶后的尾数相加减
- 尾数规格化
- 位数的舍入处理
2.浮点数的乘除运算
- 浮点数乘法运算
- 浮点数除法运算
五、运算部件的组成
- 定点运算部件
- 浮点运算部件