这几年联赛总考一些出其不意的知识点。博主发现网络流能解决的东西很多,所以这两天抽空学习了最大流dinic算法。
看着这个冠冕堂皇的名词,何为网络流?我先百度一下定义
https://baike.baidu.com/item/%E7%BD%91%E7%BB%9C%E6%B5%81/2987528?fr=aladdin
网络流(network-flows)是一种类比水流的解决问题方法,与线性规划密切相关。网络流的理论和应用在不断发展,出现了具有增益的流、多终端流、多商品流以及网络流的分解与合成等新课题。网络流的应用已遍及通讯、运输、电力、工程规划、任务分派、设备更新以及计算机辅助设计等众多领域。
什么鬼???
捕捉关键信息,发现一个词“水流”。把它理解在图中,就是在一条路径中最小的那个边权啦!

如果源点为6,终点为7的话水流1次就变成下面这个图。
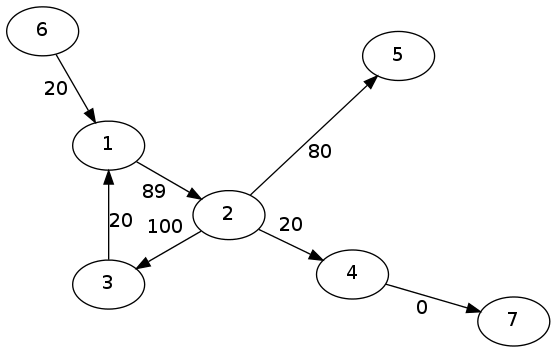
流一次6->1->2->4->7,流过10单位的水流。
但接下来原点并不能到达汇点,故最大流是10.
有的同学说:“dfs没问题!”,别急,看下一个图。
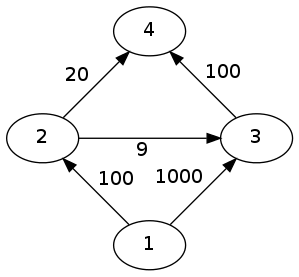
求从1到4的最大流量。
我们万一走到了这条路径1->2->3->4
变成这样
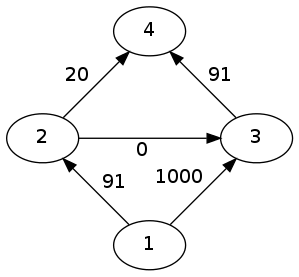
再次增广 ......
时间要炸了,这可怎么办啊?
进入今天的正题 dinic
为了解决我们上面遇到的低效方法,dinic算法引入了一个东西,叫做分层图。就是对于每一个点,我们根据从源点开始的bfs序列,为每一个点分配一个深度,然后我们进行若干遍dfs寻找增广路,每一次由u推出v必须保证v的深度必须是u的深度+1。
有用吗?
当然。
根据上面的图,从1到4
dep[1]=0,dep[2]=dep[3]=1,dep[4]=2
这样dfs每搜一次就更新一下当前流量,但如果走错了怎么办?
没关系,连一条反向边就OK了。
反向边一开始的tot要制成1,这样tot^1就能找到反向边的编号啦!
分析时间复杂度,最坏情况下为O(n2m),但是远远要优于它,因为次数是单调递减的。n<=1000的问题基本都可以解决。
另外说一下:网络流的难点是建模(真的好难),并不是实现过程。最大流BFS+DFS,费用流再用个SPFA,仅此而已。
来道USACO模版题
https://neooj.com:8082/oldoj/problem.php?id=1817
Drainage Ditches 草地排水
Description
在农夫约翰的农场上,每逢下雨,贝茜最喜欢的三叶草地就积聚了一潭水.这意味着草地被水淹没了,并且小草要继续生长还要花相当长一段时间.因此,农夫约翰修建了一套排水系统来使贝茜的草地免除被大水淹没的烦恼(不用担心,雨水会流向附近的一条小溪).作为一名一流的技师,农夫约翰
已经在每条排水沟的一端安上了控制器,这样他可以控制流入排水沟的水流量.
农夫约翰知道每一条排水沟每分钟可以流过的水量,和排水系统的准确布局(起点为水潭而终点为小溪的一张网).需要注意的是,有些时候从一处到另一处不只有一条排水沟.
根据这些信息,计算从水潭排水到小溪的最大流量.对于给出的每条排水沟,雨水只能沿着一个方向流动,注意可能会出现雨水环形流动的情形.
Input
第1 行: 两个用空格分开的整数N (0 <= N <= 200) 和 M (2 <= M <= 200).N 是农夫约翰已经挖好的排水沟的数量,M 是排水沟交叉点的数量.交点1 是水潭,交点M 是小溪.
第二行到第N+1 行: 每行有三个整数,Si, Ei, 和 Ci.Si 和 Ei (1 <= Si, Ei <= M) 指明排水沟两端的交点,雨水从Si 流向Ei.Ci (0 <= Ci <= 10,000,000)是这条排水沟的最大容量.
Output
输出一个整数,即排水的最大流量.
Sample Input
Sample Output
#include<cstdio>
#include<algorithm>
#include<cstring>
#include<queue>
using namespace std;
#define N 1000
int n,m;
int idx=1;
int head[N];
int to[N];
int val[N];
int nex[N];
int a,b,c;
int ans;
int dep[N];
int s;
void addedge(int a,int b,int c)
{
nex[++idx]=head[a];
head[a]=idx;
to[idx]=b;
val[idx]=c;
}
bool bfs()
{
queue <int> q;
q.push(1);
memset(dep,-1,sizeof(dep));
dep[1]=0;
while(!q.empty())
{
int x=q.front();
q.pop();
for(int i=head[x];i;i=nex[i])
{
if((val[i])&&dep[to[i]]==-1)
{
dep[to[i]]=dep[x]+1;
q.push(to[i]);
if(to[i]==n)
return true;
}
}
}
return false;
}
int dinic(int x,int flow)
{
int nowflow=flow;
if(x==n)
return nowflow;
for(int i=head[x];i;i=nex[i])
{
if(val[i]>0&&dep[to[i]]==dep[x]+1)
{
int now=dinic(to[i],min(val[i],nowflow));
if(now==0)
dep[to[i]]=-1;
nowflow-=now;
val[i]-=now;
val[i^1]+=now;
if(nowflow==0)
break;
}
}
return flow-nowflow;
}
int main()
{
scanf("%d%d",&m,&n);
for(int i=1;i<=m;i++)
{
scanf("%d%d%d",&a,&b,&c);
addedge(a,b,c);
addedge(b,a,0);
}
while(bfs())
ans+=dinic(1,1<<30);
printf("%d",ans);
}