动态规划算法适用于解最优化问题。通常可按以下4个步骤设计:
(1)找出最优解的性质,并刻画其结构特征;
(2)递归地定义最优值;
(3)以自底向上的方式计算出最优值;
(4)根据计算最优值时得到的信息,构造最优解。
动态规划算法的基本要素:
(1)最优子结构
当问题的最优解包含了其子问题的最优解时,称该问题具有最优子结构性质。问题的最优子结构性质提供了该问题可用动态规划算法求解的重要线索。
(2)重叠子问题
可用动态规划算法求解的问题应具备的另一个基本要素是子问题的重叠性质。在用递归算法自顶向下解此问题时,每次产生的子问题并不总是新问题,有些子问题被反复计算多次。动态规划算法正是利用了这种子问题的重叠性质,对每一个子问题只解一次,而后将其解保存在一个表格里中,当再次需要解此子问题时,只是简单地用常数时间查看一下结果。通常,不同的子问题个数随问题的大小呈多项式增长。因此,用动态规划算法只需要多项式时间,从而获得较高的解题效率。
备忘录方法
备忘录方法是动态规划算法的变形。与动态规划算法一样,备忘录方法用表格保存已解决的子问题的答案,在下次需要解此子问题时,只要简单地查看该子问题的解答,而不必重新计算。与动态规划不同的是,备忘录方法的递归方式是自顶向下的,而动态规划算法是自底向上递归的。
一般来讲,当一个问题的所有子问题都至少要解一次时,用动态规划比备忘录方法好。此时,动态规划没有任何多余的计算。当子问题空间中的部分子问题不必求解时,用备忘录方法则较有利,因为从其控制结构可以看出,该方法只解那些确实需要求解的子问题。
【最长公共子序列】
穷举搜索法是最容易想到的算法,对X的所有子序列,检查它是否也是Y的子序列,从而确定它是否为X和Y的公共子序列。并且在检查过程中记录最长的公共子序列。X的所有子序列都检查过后即可求出X和Y的最长公共子序列。若X共有m个元素组成,它共有2m个不同的子序列,从而穷举搜索法需要指数时间。
下面按照动态规划算法设计的步骤来设计解此问题:
1.最长公共子序列的结构
事实上,最长公共子序列问题具有最优子结构性质。
设X={x1,x2,...,xm}和Y={y1,y2,...,yn}的最长公共子序列为Z={z1,z2,...,zk},则
(1)若xm=yn,则zk=xm=yn,且Zk-1是Xm-1和Yn-1的最长公共子序列;
(2)若xm≠yn,且zk≠xm,则Z是Xm-1和Y的最长公共子序列;
(3)若xm≠yn,且zk≠yn,则Z是X和Yn-1的最长公共子序列。
由此可见,两个序列的最长公共子序列包含了这两个序列的前缀的最长公共子序列。
2.子问题的递归结构
用c[i][j]记录序列Xi和Yj的最长公共子序列的长度。由最优子结构性质可建立递归关系如下:
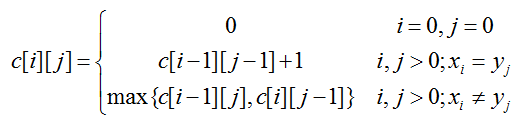
3.计算最优值
void LCSLength( int m, int n,char * x,char * y,int ** c,int ** b) {//c[i][j]存储Xi和Yj最长公共子序列长度,b[i][j]记录c[i][j]的值是由哪一个子问题解得的 int i,j; for( i = 1; i <= m; i++) c[i][0]=0; for( j = 1; j <= n; j++) c[0][j]=0; for( i = 1; i <= m; i++) for( j = 1; j <= n; j++){ if( x[i] == y[j]) { c[i][j] = c[i-1][j-1] + 1; b[i][j] = 1; } else if( c[i-1][j] > c[i][j-1]) { c[i][j] = c[i-1][j]; b[i][j] = 2; } else { c[i][j] = c[i][j-1]; b[i][j] = 3; } } }
由于每个数组的单元的计算耗时为O(1)时间,算法LCSLength耗时O(mn)。
4.构造最长公共子序列
根据LCSLength算法中b的内容打印最长公共子序列。
void LCS( int i, int j, char * x, char * b ) { if( i == 0 || j == 0) return ; if( b[i][j] == 1) { LCS(i-1,j-1,x,b); cout<<x[i]; } else if( b[i][j] == 2) LCS(i-1,j,x,b); else LCS(i,j-1,x,b); }
在算法LCS中,每一次递归调用使i或j减1,因此算法的计算时间为O(m+n)。
【最大子段和】
给定由n和整数组成的序列a1,a2,...,an,求该序列形如∑ak的子段和的最大值。
1.简单算法
void MaxSum( int n, int * a, int & besti, int & bestj) { int sum = 0; for( int i = 1; i <= n; i++) for( int j = i; j <= n; j++){ int thissum = 0; for( int k = i; k <= j; k++) thissum+=a[k]; if( thissum > sum){ sum = thissum; besti = i; bestj = j; } } return sum; }
三个for循环可以看出,它需要的计算时间是O(n3)。第三个for循环可以省去,避免重复计算,改进后的算法如下:
void MaxSum( int n, int * a, int & besti, int & bestj) { int sum = 0; for( int i = 1; i <= n; i++){ int thissum = 0; for( int j = i; j <= n; j++){ thissum+=a[j]; if( thissum > sum){ sum = thissum; besti = i; bestj = j; } } } return sum; }
改进后只需要O(n2)的计算时间。
2.分治算法
从问题的解得结构可以看出,它适合用分治法求解。
如果将所给序列a[1:n]分为两个两段a[1:n/2]和a[n/2+1:n],分别求出这两段的最大子段和,则a[1:n]的最大子段和有三种情形:
(1)a[1:n]的最大子段和与a[1:n/2]的最大子段和相同;
(2)a[1:n]的最大子段和与a[n/2+1:n]的最大子段和相同;
(3)a[1:n]的最大子段和为∑ak,且1≤i≤n/2,n/2+1≤j≤n。
对于(3)的情况,在a[1:n/2]中计算出s1[i:n/2]的最大和,并在a[n/2+1:n]中计算出s2[n/2+1:j]的最大和。则s1+s2就是1情况(3)的最优值。
void MaxSubSum( int * a, int left, int right) { int sum = 0; if( left == right ) sum = a[left] > 0 ? a[left] : 0; else { int center = (left + right) / 2; int leftsum = MaxSubSum( a,left,center); int rughtsum = MaxSubSum(a,center+1,right); int s1 = 0; int lefts = 0; for( int i = center; i >= left; i--){ lefts += a[i]; if( lefts > s1) s1 = lefts; } int s2 = 0; int rights = 0; for( int i = center+1; i <= right; i++){ rights += a[i]; if( rights > s2) s2 = rights; } sum = s1 + s2; if( sum < leftsum) sum = leftsum; if( sum < rightsum) sum = rightsum; } return sum; }
解此递归方程可知,所需时间为O(nlogn)。
3.动态规划算法
b[j]表示包含a[j]及其之前的任意个元素的最大子段和。b[j]与b[j-1]的关系表示如下:
b[j]=max{b[j-1]+a[j],a[j]},1≤j≤n
void MaxSum( int n, int * a) { int sum = 0; for( int i = 1; i < n; i++ ) { if( b > 0 ) b += a[i]; else b = a[i]; if( b > sum ) sum = b; } return sum; }
上述算法显然需要O(n)计算时间和O(n)空间。
4.最大子段和问题与动态规划算法的推广
(1)最大矩阵和问题:给定一个m行n列的整数矩阵A,试求矩阵A的一个子矩阵,使其各元素之和最大。
如果直接用枚举的方法解最大子矩阵和问题,需要O(m2n2)时间。
用动态规划算法设计:
b[j]=∑a[i][j],且i1≤i≤i2,则t(i1,i2)=max∑b[j],且j1≤j≤j2。
int MaxSumTwo( int m, int n, int * a) { int sum = 0; int * b = new int [n+1]; for( int i = 1; i <= m; i++ ){ for( int k = 1; k <= n; k++ ) b[k] = 0; for( int j = i; j <= m; j++){ for( int k = 1; k <= n; k++) b[k] += a[j][k]; int max = MaxSum(n,b); if( max > sum) sum = max; } } return sum; }
MaxSumTwo算法需要O(m2n)时间。
(2)最大m子段和问题:给定由n个整数组成的序列,以及一个正整数m,要求确定序列的m个不想交子段,使这m个子段的总和达到最大。
设b(i,j)表示数组a的前j项中i个子段和的最大值,且第i个子段含a[j],则所求的最优值显然为max b(m,j)。与最大子段和问题类似,计算b(i,j)的递归式为:
b(i,j)=max{b(i,j-1)+a[j],max b(i-1,t)+a[j]}
其中b(i,j-1)+a[j]中a[j]包含在第i个子段内;max b[i-1,j]+a[j]中a[j]为单独的一个子段,即第i个子段只有一个元素。
void MaxSum( int m, int n, int * a) { if( n < m || m < 1) return 0; int * * b = new int * [m+1]; for( int i = 0; i <= m; i ++ ) b[i] = new int [n+1]; for( int i = 0; i <= m; i ++) b[i][0] = 0; for( int j = o; j <= n; j ++ ) b[0][j] = 0; for( int i = 0; i <= m; i ++) for( int j = 0; j <= n; j ++) if( j > i){ b[i][j] = b[i][j-1] +a[j]; for( int k = i-1; k < j; k ++) if( b[i][j] < b[i-1][k] + a[j]) b[i][j] = b[i-1][k] + a[j]; } else b[i][j] = b[i-1][j-1] + a[j]; int sum = 0; for( int j = m;j <= n; j ++) if( sum < b[m][j]) sum = b[m][j]; return sum; }
上述算法显然需要O(mn2)计算时间和O(mn)空间。
计算b[i][j]时只用到数组b的第i-1和i行的值,可以减少需要的空间;max b(i-1,t)的值可以在计算第i-1行时预先计算并保存起来,节省了时间。
void MaxSum( int m, int n, int * a) { if( n < m || m < 1) return 0; int * b = new int * [n+1]; int * c = new int * [n+1]; b[0] = 0; c[1] = 0; for( int i = 1; i <= m; i ++ ){ b[i] = b[i-1] + a[i]; c[i-1] = b[i]; int max = b[i]; for( int j = i; j <= i+n-m; j ++){ b[j] = b[j-1] > c[j-1] ? b[j-1]+a[j] : c[j-1] +a[j]; c[j-1] = max; if( max < b[j] ) max = b[j]; } c[i+n-m] = max; } int sum = 0; for( int j = m;j <= n; j ++) if( sum < b[m][j]) sum = b[m][j]; return sum; }
【0-1背包】
问题描述:给定n种物品和一个背包。物品i的重量是wi,其价值是vi,背包的容量是c。问应如何选择装入背包中的物品,使得装入背包中的物品的总价值最大?
0-1背包问题是一个特殊的整数规划问题。
1.最优子结构性质
设(y1,y2,...,yn)是所给0-1背包问题的最优解,则(y2,y3,...yn)是c-w1问题的最优解。因若不然,设(z2,z3,...zn)是c-w1的一个最优解,而(y2,y3,...yn)不是它的最优解。由此可以说明(y1,z2,...,zn)是所给问题的一个更优解,从而(y1,y2,...,yn)不是所给问题的最优解。此为矛盾。
2.递归关系
m(i,j)是背包容量为j,可选择物品为i,i+1,...,n是0-1背包问题的最优值。递归式如下:
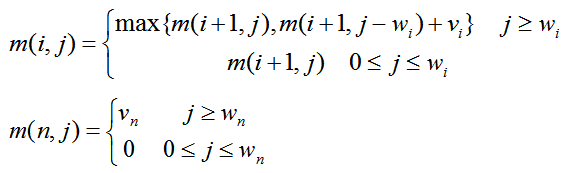
m(i,j)分为两种情况,容量不够直接用m(i+1,j)填写,容量够时需要比较放入和不放入的价值大小决定是否装入。
3.算法描述
当wi为正整数时,用二维数组m[][]来存储m(i,j)的相应值。算法如下:
template< class Type > void Knapsack( Type v, int w, int c, int n, Type * * m ) { int jMax = min( w[n]-1, c ); for( int j = 0; j <= jMax; j++ ) m[n][j] = 0; for( int j = w[m]; j <= c; j++ ) m[n][j] = v[n]; for( int i = n -1; i >1; i-- ){ jMax = min( w[i]-1, c ); for( int j = 0; j <= jMax; j++ ) m[i][j] = m[i+1][j]; for( int j = w[m]; j <= c; j++ ) m[i][j] = max(m[i+1][j],m[i+1][j-w[i]]+v[i]); } m[1][c] = m[2][c]; if( c >= w[1] ) m[1][c] = max( m[1][c],m[2][c-w[1]]+v[1]); } template< class Type> void Traceback( Type ** m, int w, int c, int n, int x ) { for( int i = 1; i < n; i++ ) if( m[i][c]==m[i+1][c]) x[i] = 0; else { x[i] = 1; c -= w[i]; } x[n] = ( m[n][c]) ? 1 : 0; }
按上述算法Knapsack计算后,m[1][c]给出所要求的0-1背包问题的最优值。相应的最优解可由算法Traceback计算得出。
4.计算复杂度分析
从计算m(i,j)的递归式容易看出,Knapsack算法需要O(cn)计算时间,如果c很大时,算法需要的计算时间就会变得很多。这一点需要克服,还有一点,就是物品的重量不一定是整数。
改进的动态规划算法(今天先写到这,明天继续更新)。