位图与布隆及大数据处理题型分析

1.位图

由题引入：

【腾讯】：2.给40亿个不重复的无符号整数，没排过序。给一个无符号整数，如何快速判断一个数是否在这40亿个数中。

如果将40亿个数按整型放入内存，显然不科学，就算内存足够，这样做也是浪费空间。

解决思路：用一个比特位表示一个数，存在的话该位上就置为1，不在的话置为0；这样40亿个数需要40亿个比特位，换算一下也就是500M，相对于16G来说，大大节省了空间。

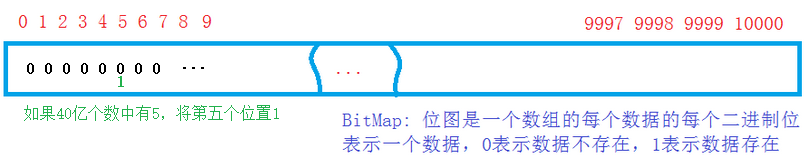
注意：位图只适合判断，查找数据是否存在，且只能对整数进行处理。

代码如下：

class BitMap
{
public:
    BitMap(size_t range)
        :_size(0)
    {  
        _a.resize((range >> 5) + 1);  //多少个整型，一个整型表示32个数，加一是至少一个整型
    }
    void Set(size_t value) //存在时置1
    {
        size_t index = value >> 5;  //计算在哪个数据上
        size_t num = value % 32;  //计算在第几个位上
        (_a[index]) |= (1 << num);  //将该位置1
        _size++;
    }
    void Rset(size_t value)  //不存在时或删除一个数时置0
    {
        size_t index = value >> 5;  //计算在哪个数据上
        size_t num = value % 32;  //计算在第几个位
        (_a[index]) &= (~(1 << num));  //将该位置1
        _size--;
    }
    bool JudgeBit(size_t value)  //判断该位的数值
    {
        size_t index = value >> 5;  
        size_t num = value % 32;
        bool flag = (_a[index]) & (1 << num);//flag为1即存在
        return flag;
    }
private:
    vector<int> _a;  //保存数据的数组
    size_t _size;    //数组中一共存在的数的总数
};

void BitMapTest()
{
    BitMap bit(4000000000);
    bit.Set(12000);
    bit.Set(1200);
    bit.Set(1205590);
    bit.Set(12001);
    bit.Set(12002);
    bit.Set(12003);
    bit.Set(12005);
    cout << bit.JudgeBit(12090) << endl;
    cout << bit.JudgeBit(120920) << endl;
    cout << bit.JudgeBit(1205590) << endl;
}

int main()
{
    BitMapTest();
    getchar();
    return 0;

优点：（1）相对来说节省了不少空间。当需要处理的数量级较大时，这个优点显露无疑。

（2）查找、删除效率高。位图只是在创建的时候开辟空间消耗时间，但是当位图创建完成后查找、删除只需一步操作。

2、布隆过滤器

 很明显，用位图只能用来处理整型，如果遇到字符型或者其他类型的文件就无能为力了，所以布隆过滤器就上场了。

　　布隆过滤器是由布隆在1970年提出的。它实际上是由一个很长的二进制向量（运用位图思想）和一系列随机映射函数（哈希函数）组成，布隆过滤器可以用于检索一个元素是否在一个集合中。详细来说就是将字符类型的数据通过哈希字符串函数转换成整数，然后用位图思想将一个数据用一个比特位表示起来。但是这样做有一个缺点，就是判断不准确，因为没有一种算法可以将字符串准确转换为唯一表示这个字符数据的整数。另外Hash面临的问题就是冲突。假设 Hash 函数是良好的，如果我们的位阵列长度为 m 个点，那么如果我们想将冲突率降低到例如 1%, 这个散列表就只能容纳 m/100 个元素。显然这就不叫空间有效了（Space-efficient）。这里提出一种改进方法：运用多种不同的哈希函数对同一字符数据进行转化，将它们的转换结果都存在表示在比特位中，那么判断的时候当这几种哈希转换结果表示的位都为1时，字符数据存在，只要有一种方法转化的位为0，即不存在。简单来说，就是多个 Hash中，如果它们有一个说元素不在集合中，那肯定就不在。如果它们都说在，虽然也有一定可能性它们在说谎，不过直觉上判断这种事情的概率是比较低的。

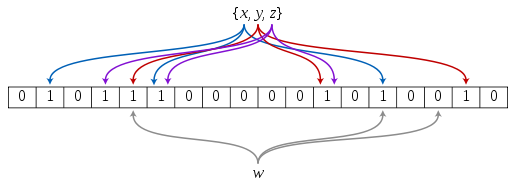
优点

　　相比于其它的数据结构，布隆过滤器在空间和时间方面都有巨大的优势。布隆过滤器存储空间和插入/查询时间都是常数；另外, Hash 函数相互之间没有关系，方便由硬件并行实现；布隆过滤器不需要存储元素本身，在某些对保密要求非常严格的场合有优势；布隆过滤器可以表示全集，其它任何数据结构都不能；k 和 m 相同，使用同一组 Hash 函数的两个布隆过滤器的交并差运算可以使用位操作进行。

缺点

　　布隆过滤器的缺点和优点一样明显。误算率是其中之一。随着存入的元素数量增加，误算率随之增加。但是如果元素数量太少，则使用散列表足矣。另外，一般情况下不能从布隆过滤器中删除元素。 我们很容易想到把位列阵变成整数数组，每插入一个元素相应的计数器加1, 这样删除元素时将计数器减掉就可以了。然而要保证安全的删除元素并非如此简单。首先我们必须保证删除的元素的确在布隆过滤器里面。 这一点单凭这个过滤器是无法保证的。另外计数器回绕也会造成问题。

示例代码如下：

//各类哈希函数  
size_t BKDRHash(const char *str)
{
    register size_t hash = 0;
    while (size_t ch = (size_t)*str++)
    {
        hash = hash * 131 + ch;
    }
    return hash;
}

size_t SDBMHash(const char* str)
{
    register size_t hash = 0;
    while (size_t ch = (size_t)*str++)
    {
        hash = 65599 * hash + ch;
    }
    return hash;
}
size_t RSHash(const char * str)
{
    size_t hash = 0;
    size_t magic = 63689;
    while (size_t ch = (size_t)*str++)
    {
        hash = hash * magic + ch;
        magic *= 378551;
    }
    return hash;
}
size_t APHash(const char*str)
{
    register size_t hash = 0;
    size_t ch;
    for (long i = 0; ch = (size_t)*str++; i++)
    {
        if ((i & 1) == 0)
        {
            hash ^= ((hash << 7) ^ ch ^ (hash >> 3));
        }
        else
        {
            hash ^= (~((hash << 11) ^ ch ^ (hash >> 5)));
        }
    }
    return hash;
}
size_t JSHash(const char* str)
{
    if (!*str)
    {
        return 0;
    }
    size_t hash = 1315423911;
    while (size_t ch = (size_t)*str++)
    {
        hash ^= ((hash << 5) + ch + (hash >> 2));
    }
    return hash;
}

//哈希函数对应的仿函数
 template<class K>
 struct __HashFunc1
 {
     size_t operator()(const K& key)
     {
         return BKDRHash(key.c_str());
     }
 };
 template<class K>
 struct __HashFunc2
 {
     size_t operator()(const K& key)
     {
         return SDBMHash(key.c_str());
     }
 };
 template<class K>
 struct __HashFunc3
 {
     size_t operator()(const K& key)
     {
         return RSHash(key.c_str());
     }
 };
 template<class K>
 struct __HashFunc4
 {
     size_t operator()(const K& key)
     {
         return APHash(key.c_str());
     }
 };
 template<class K>
 struct __HashFunc5
 {
     size_t operator()(const K& key)
     {
         return JSHash(key.c_str());
     }
 };
 
 template < class K = string,
     class HashFunc1 = __HashFunc1<K>,
     class HashFunc2 = __HashFunc2<K>,
     class HashFunc3 = __HashFunc3<K>,
     class HashFunc4 = __HashFunc4<K>,
     class HashFunc5 = __HashFunc5<K>>
 class BloomFilter
 {
 public:
     BloomFilter(size_t range)
         :_range(range)
     {
         _bitmap._a.resize((range >> 5) + 1);  //初始空间
     }
     void _Set(const K& key )
     {
        _bitmap.Set(HashFunc1()(key) % _range);
        _bitmap.Set(HashFunc2()(key) % _range);
        _bitmap.Set(HashFunc3()(key) % _range);
        _bitmap.Set(HashFunc4()(key) % _range);
        _bitmap.Set(HashFunc5()(key) % _range);
     }
    bool _JudgeBit(const K& key)
    {
        if (!_bitmap.JudgeBit(HashFunc1()(key) % _range))//只要有一个匹配不上就不存在
            return false;
        if (!_bitmap.JudgeBit(HashFunc2()(key) % _range))
            return false;
        if (!_bitmap.JudgeBit(HashFunc3()(key) % _range))
            return false;
        if (!_bitmap.JudgeBit(HashFunc4()(key) % _range))
            return false;
        if (!_bitmap.JudgeBit(HashFunc5()(key) % _range))
            return false;
        return true;
    }
 private:
     BitMap _bitmap;  //用位图表示转换后的数
     size_t _range;  //
 };

3、大数据处理问题

1.给一个超过100G大小的log file, log中存着IP地址, 设计算法找到出现次数最多的IP地址？!
2.与上题条件相同，如何找到top K的IP？如何直接用Linux系统命令实现？!
3.给定100亿个整数，设计算法找到只出现一次的整数!
4.给两个文件，分别有100亿个整数，我们只有1G内存，如何找到两个文件交集!
5.1个文件有100亿个int，1G内存，设计算法找到出现次数不超过2次的所有整数!
6.给两个文件，分别有100亿个url，我们只有1G内存，如何找到两个文件交集？分别给出精确 算法和近似算法!
7.如何扩展BloomFilter使得它支持删除元素的操作？如何扩展BloomFilter使得它支持计数操作？!
8.给上千个文件，每个文件大小为1K—100M。给n个词，设计算法对每个词找到所有包含它文 件，你只有100K内存!
9.有一个词典，包含N个英文单词，现在任意给一个字符串，设计算法找出包含这个字符串的所 有英文单词!

 第1题、给一个超过100G大小的log file, log中存着IP地址, 设计算法找到出现次数最多的IP地址

　　这是一个大小为100G的一个日志文件，主要问题就是一般的计算机内存肯定放不下；第一个想到的办法就是切分，把100G的文件切成100份，然后把这100个文件当作是大小为100的哈希表，而每份只有1G的大小，就可以依次读入内存进行处理。题目要求是：找到出现次数最多的IP地址，那么文件中肯定存在大量的相同IP地址，思路是让相同的IP存入同一文件，这时又要用到哈希字符串函数，就是上面布隆过滤器用到的转换函数，由相同的IP转换得到的key值一定相同，然后根据index = key%100决定存在于哪一个文件中，而相同的IP也就进入了同一个文件。

　　然后对单个文件进行处理，找出这个文件中出现次数最多的IP，以IP为key值，value记录出现的次数，用key_value结构的搜索树就可以很快找出来，然后用MAX记录下来，读入下一个文件，然后比较MAX值，遇到更大的就更新,最后得到的MAX就是这个100G文件中出现次数最多的IP地址。

这个题目中的重点思想就是哈希切分。

第2题、一个超过100G大小的log file, 存着IP地址，找到top K的IP。如何直接用Linux系统命令实现？

　　这一题条件同上一题，不同的是由求次数最多的一个改为求次数最多的前K个。思路同上题，哈希切分然后用堆排序，还是以IP为key值，然后统计各个文件中每个IP出现的次数（方法同第一题，也就是说每个文件建一颗搜索树）， 然后取其中的K个（key_value结构）结点以次数建一个最小堆；然后将其余的节点依次与堆顶节点比较，如果大于堆顶节点，与其一换，交换之后对堆进行一次向下调整，保证堆顶元素仍是堆中最小，直到所有IP都比较完。然后堆中的就是top K个IP了。

这题是个典型的top K问题，重点是建小堆，然后交换堆顶元素。

第3题、给定100亿个整数，找到只出现一次的整数

　　与上面同样的一个问题是100亿整数这样一个庞大的数字，大约是35G的大小。但是整数能表示的最大范围也就是2的32次方 那么大约就是16G的大小，那么剩下的就都是重复的数，这道题没有规定死内存大小，但是16G还是比较大，浪费内存资源，如何继续缩小内存，还是利用位图思想。与前例腾讯笔试题不同的是，这里需要区分更多的状态，我们需要表示的状态有：00不存在， 01出现一次，10出现多次（>=2次），11不表示。也就是说我们需要用两个比特位来表示一个数的状态，然后遍历一遍位图找到状态为01的数，就是只出现一次的整数。

这个题重点是两个比特位的位图思想。

第4题、两个文件，分别有100亿个整数，我们只有1G内存，找到两个文件的交集

　　此题初始思路同上，建立位图，不在赘述，这里主要讲求交集。可以对其中一个文件建立位图，然后从另一个文件中依次取数据，判断是否在位图中。数据判断完存在的即为交集。另一种思路，如果这里还有1G的内存的话，可以给两个文件分别键位图，然后比较对应的数据位。

　　第二种方法是哈希切分，将两个文件都切分为1000小份，每个文件的大小就几十兆的样子，分别对两个对文件里的整数进行哈希分配，即将所有整数模除1000，使相同的数进入相同的文件，然后分别拿A哈希切分好的第一个文件和B哈希切分好的第一个文件对比，找出交集存到一个新文件中，依次类推，直到2000个文件互相比较完。

这个题重点是位图思想和哈希切分。

第5题、1个文件有100亿个int，1G内存，找到出现次数不超过2次的所有整数

　　这个题思路同第三题，用两个比特位表示的位图，我们需要表示的状态有：00不存在， 01出现1次，10出现2次，11出现多次（>2次）。

这个题重点也是两个比特位的位图思想。

第6题、两个文件，分别有100亿个url，我们只有1G内存，找到两个文件交集，分别给出精确算法和近似算法。

　　与第四题类似只是这里存的是URL，所以要用布隆过滤器。近似算法是，将一个文件内容存到布隆过滤器中，方法如上面介绍的布隆过滤器中的一样，然后从另一个文件中一个个的取URL判断是否在布隆中存在的就是交集。为什么布隆过滤器是近似算法，是因为它的不存在是确定的，存在是不确定的，即一个字符串对应5个位， 如果有一个位为0，则这字符串肯定不存在，如果一个字符串对应的5个位都为1，但是这个字符串却不 一定存在，因为可能这5个位都是被其它字符串的对应位置为1的，这就是其中的哈希冲突问题。

精确算法同第四题的方法二，哈希切分。

第7题、扩展BloomFilter使得它支持删除元素的操作或支持计数操作

　　因为布隆过滤器的一个Key对应多个位，所以如果要删除的话，就会有些麻烦，不能单纯的将对应位全部置为0，因为可能还有其它key对应这些位，所以，需要对每一个位进行引用计数，以实现删除的操作。因为需要每一个对应位都需要一个计数，所以每一位至少需要一个int，那么我们就不得不放弃位图了，也就是放弃了最小的空间消耗，我们需要直接以一个就像数组一样的实现，只不过数组的内容存放的是引用计数。

代码示例如下：

 //支持引用计数，可以删除元素的布隆
 template <class K = string>
 class NumBloom
 {
     size_t HashFunc1(const K& key)
     {
         const char* str = key.c_str();
         unsigned int seed = 131;
         unsigned int hash = 0;
         while (*str)
         {
             hash = hash*seed + (*str++);
         }
         return(hash & 0x7FFFFFFF);
     };
     size_t HashFunc2(const K& key)
     {
         const char* str = key.c_str();
         register size_t hash = 0;
         while (size_t ch = (size_t)*str++)
         {
             hash = 65599 * hash + ch;
             //hash = (size_t)ch + (hash << 6) + (hash << 16) - hash;  
         }
         return hash;
     }
     size_t HashFunc3(const K& key)
     {
         const char* str = key.c_str();
         register size_t hash = 0;
         size_t magic = 63689;
         while (size_t ch = (size_t)*str++)
         {
             hash = hash * magic + ch;
             magic *= 378551;
         }
         return hash;
     }
     size_t HashFunc4(const K& key)
     {
         const char* str = key.c_str();
         register size_t hash = 0;
         size_t ch;
         for (long i = 0; ch = (size_t)*str++; i++)
         {
             if ((i & 1) == 0)
             {
                 hash ^= ((hash << 7) ^ ch ^ (hash >> 3));
             }
             else
             {
                 hash ^= (~((hash << 11) ^ ch ^ (hash >> 5)));
             }
         }
         return hash;
     }
     size_t HashFunc5(const K& key)
     {
         const char* str = key.c_str();
         if (!*str)
             return 0;
         register size_t hash = 1315423911;
         while (size_t ch = (size_t)*str++)
         {
             hash ^= ((hash << 5) + ch + (hash >> 2));
         }
         return hash;
     }
 public:
     NumBloom(const size_t range)
     {
         _bloom.resize(range);  //初始空间
         for (size_t i = 0; i < _bloom.size(); i++)
         {
             _bloom[i] = 0;
         }
     }
     void _Set(const K& key)
     {
         _bloom[HashFunc1(key) % _bloom.size()];
         _bloom[HashFunc1(key) % _bloom.size()];
         _bloom[HashFunc1(key) % _bloom.size()];
         _bloom[HashFunc1(key) % _bloom.size()];
         _bloom[HashFunc1(key) % _bloom.size()];
         _bloom[HashFunc1(key) % _bloom.size()];
     }
     void _Reset(const K& key)
     {
         if (_bloom[HashFunc1(key) % _bloom.size()] == 0)
             return false;
         if (_bloom[HashFunc2(key) % _bloom.size()] == 0)
             return false;
         if (_bloom[HashFunc3(key) % _bloom.size()] == 0)
             return false;
         if (_bloom[HashFunc4(key) % _bloom.size()] == 0)
             return false;
         if (_bloom[HashFunc5(key) % _bloom.size()] == 0)
             return false;
         _bloom[HashFunc1(key) % _bloom.size()]--;
         _bloom[HashFunc2(key) % _bloom.size()]--;
         _bloom[HashFunc3(key) % _bloom.size()]--;
         _bloom[HashFunc4(key) % _bloom.size()]--;
         _bloom[HashFunc5(key) % _bloom.size()]--;
     }
     bool _JudgeBit(const K& key)
     {
         if (_bloom[HashFunc1(key) % _bloom.size()] == 0)//只要有一个匹配不上就不存在
             return false;
         if (_bloom[HashFunc2(key) % _bloom.size()] == 0)//只要有一个匹配不上就不存在
             return false;
         if (_bloom[HashFunc3(key) % _bloom.size()] == 0)//只要有一个匹配不上就不存在
             return false;
         if (_bloom[HashFunc4(key) % _bloom.size()] == 0)//只要有一个匹配不上就不存在
             return false;
         if (_bloom[HashFunc5(key) % _bloom.size()] == 0)//只要有一个匹配不上就不存在
             return false;
         return true;
     }

 private:
     vector<size_t> _bloom;
 };

第8题、给上千个文件，每个文件大小为1K—100M。给n个词，设计算法对每个词找到所有包含它的文件，你只有100K内存!

牛客网上的解析：

0: 用一个文件info 准备用来保存ｎ个词和包含其的文件信息。
1 : 首先把ｎ个词分成ｘ份。对每一份用生成一个布隆过滤器（因为对ｎ个词只生成一个布隆过滤器，内存可能不够用）。把生成的所有布隆过滤器存入外存的一个文件Filter中。２：将内存分为两块缓冲区，一块用于每次读入一个布隆过滤器，一个用于读文件(读文件这个缓冲区使用相当于有界生产者消费者问题模型来实现同步)，大文件可以分为更小的文件，但需要存储大文件的标示信息（如这个小文件是哪个大文件的）。
３：对读入的每一个单词用内存中的布隆过滤器来判断是否包含这个值，如果不包含，从Filter文件中读取下一个布隆过滤器到内存，直到包含或遍历完所有布隆过滤器。如果包含,更新info 文件。直到处理完所有数据。删除Filter文件。
备注：
１：关于布隆过滤器：其实就是一张用来存储字符串hash值的BitMap.
２：可能还有一些细节问题，如重复的字符串导致的重复计算等要考虑一下。
第9题、有一个词典，包含N个英文单词，现在任意给一个字符串，设计算法找出包含这个字符串的所 有英文单词!

思路：用kmp算法或者字典树，KMP算法可见我的另一篇文章：字符串模式匹配问题