学号 20172326 《程序设计与数据结构》第八周学习总结
教材学习内容总结
堆
- 最小堆 是一棵完全树。对每一结点,它小于或等于其左孩子和右孩子。同理,也存在最大堆,其结点大于或等于他的左右孩子。
- 所具有的的方法(其继承了BinaryTree的方法)
addElement
removeMin
findMin
-
addElement 插入操作。如果不进行比较,插入元素可能会导致堆不符合规则。在保证其始终为完全树的基础上,根据最小堆或者最大堆进行填充。同时,根据其最大堆或最小堆的性质,插入时需要与其父结点以及孩子结点进行比较,例如,对于一个最小堆,如果发现有孩子结点小于待插入结点或其小于其父结点,此时就需要进行调换位置。
-
因此,对最后一个结点进行记录,来确定新插入结点的位置以及其他信息。
-
插入元素的几种情况。由于记录了最后一个结点,因此我们每次默认从最后一个结点开始1.最后一个结点时右子树的右结点。此时,最小堆为满树,直接将带插入结点插入左子树最左结点即可。2.最后结点为右子树的左结点,此时,将带插入结点插入其兄弟位置,即右子树的右孩子位置。3.位于左子树的左孩子,直接将其插入其兄弟位置即可。4.最后结点为左子树的右结点。那么将带插入结点插入至最后结点的父结点的兄弟结点的左孩子位置即可。这个情况是最复杂的。
-
removeMin操作。因为根据定义,堆的根要么是最大的,要么是最小的。因此,尤其是最小堆。这个操作就相当于删除根。删除的同时需要找到堆中其他元素来进行替换,且这个元素时唯一的,也就是树中的最末一片叶子上的元素。
-
findMin很简单,就不在此赘述
-
调整重排序,当建立起一个二叉树后,如果需要将其转化为一个最小堆,那么就要经过数个步骤。
1.调整过程中,总是将根结点(被调整结点)与左右孩子比较;
2.不满足堆条件时,将根结点与左右孩子中较大者交换;
3.这个调整过程一直进行到所有子树都是堆或者交换到叶子为止。从哪个结点开始呢?根据经验,从第n/2个元素开始,若n为奇数,择不保留小数。依次递减。例如,n为8,则从第四个开始,然后从第三个,第二个依次与子结点比较。每经过一次比较,都能找出现有树的一个最小值。 -
顺带一提,在数据空间中同样也有堆栈一说,但与我们现在所学的数据结构的堆和栈有很大区别
教材学习中的问题和解决过程
- 问题1:最小堆的删除问题
- 问题1理解:书上的内容一开始就迷惑了我一下,
当然我也看的不是很仔细删除时,直接将根移除,之后把最后结点放到根处就行。这就结束了?如何保证最后结点就是最小的呢?带着疑惑,继续往下看,同时,结合代码,我逐渐理清了思路。移除根是removeMin的直接目的,所以我们要删除根。但把根删了不能拍屁股走人,总有结点要补上去。为了维护这个最小堆,至少要保证其是一个完全树,因此,我们就把最后结点拿出来,放到根的位置。因为最后结点的移除是不会改变其完全树的性质。完成这一步后,在保证了其树的基础上,再对其进行重新排序。与插入结点的情况类似,当最后结点为右子树的右结点时,直接放至根处即可。当最后结点为右子树的左结点时,同样,直接放至根处即可。当最后结点为左子树的左结点时,直接放至根结点就行。 - 问题2:最小堆怎样提供了一个高效的优先级队列实现?
- 问题2理解:首先明确何为优先级队列。第一,具有更高优先级的项目在先。第二具有相同优先级项目使用先进先出方法来确定其排序。显然堆不是一个队列。而且,他甚至不是线性结构,但正因为其非线性结构,使得在各方面都有方便之处。例如,一个普通的队列,只能在两端进行插入删除操作。但是作为非线性数据结构的堆(树)便不受这种限制。根据优先度可随意插入删除元素,且有着高效的查找效率。因此,从多个角度来说,其都是一种高效的优先级队列实现。
代码调试中的问题和解决过程
- 问题:pp12.1的实现问题
- 问题解决方案:用堆实现队列。队列需要先进先出,用堆怎样实现?和别的同学交流一波并结合自己的理解,我有了这几种思路。第一种,利用书上的优先级队列进行实现。例如,我先输入五个数,则第一个输入的数的优先级为5,依次类推。也就是说,利用优先级来代表那个最先出来。因为不存在同时两个数进入数组,所以也就不会出现优先级相同的情况。
public void addElement(T object, int priority)
{
PrioritizedObject<T> obj = new PrioritizedObject<T>(object, priority);
super.addElement(obj);
}
public T removeNext()
{
PrioritizedObject<T> obj = (PrioritizedObject<T>)super.removeMin();
return obj.getElement();
}
测试类是这样的
PriorityQueue pq= new PriorityQueue();
pq.addElement("a",1);
pq.addElement("b",2);
pq.addElement("c",3);
pq.addElement("o",4);
pq.addElement("g",5);
pq.addElement("cyka bylat",6);
System.out.println(pq.removeNext());
pq.addElement("edd mounted",5);
System.out.println(pq.removeNext());
运行结果是这样的
-
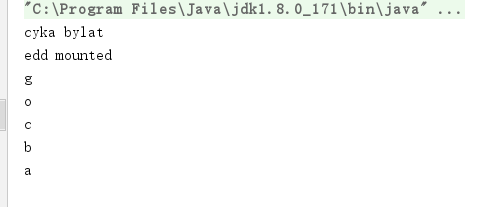
-
第二种思路呢,就是以已有的LinkedHeap为基础,加上一个变量,这个变量的意义就是确定先后顺序,毕竟,堆不能被限制只能在两端操作,那么我们就以其先后顺序为其结点的比较值。详细地说,我输入一组数“55,23,78,66,12”那么第一个输入的数55的order为1,依次类推。同时,不能忘记的是,我们恰恰是使用小顶堆实现的,所以移除元素时,将小order的先出。将removeMin略加改造就行了。
public void addElement(T obj)
{
HeapNode<T> node = new HeapNode<T>(obj);
node.setOrder(count);
count++;
if (root == null)
root=node;
else
{
HeapNode<T> nextParent = getNextParentAdd();
if (nextParent.getLeft() == null)
nextParent.setLeft(node);
else
nextParent.setRight(node);
node.setParent(nextParent);
}
lastNode = node;
modCount++;
if (size() > 1)
heapifyAdd();
}
这里就是关键代码,删除部分基本没什么变化。就不赘述了
代码托管
上周考试错题总结
- 错题1及原因,理解情况
- After one pass on the numbers ( 5 3 9 5 ), what would be the result if you were to use Bubble Sort?
- 一次排序,将大的排至最后所以就有5395->3595->3559
- 错题2及原因,理解情况
- Insertion sort is an algorithm that sorts a list of values by repetitively putting a particular value into its final, sorted, position.
- 插入排序就是每次将最小的元素排至最前,对已经排好的元素,不存在重复排序。
- 错题3及原因,理解情况
- One of the uses of trees is to provide simpler implementations of other collections.
- 这道题我真的不懂,待我问问
其他(感悟、思考等,可选)
- 堆的学习还行,主要是利用了树的性质,然后有了一些有趣的性质
学习进度条
| 代码行数(新增/累积) | 博客量(新增/累积) | 学习时间(新增/累积) | 重要成长 | |
|---|---|---|---|---|
| 目标 | 5000行 | 30篇 | 400小时 | |
| 第一周 | 0/0 | 1/1 | 3/3 | |
| 第二周 | 409/409 | 1/2 | 5/8 | |
| 第三周 | 1174/1583 | 1/3 | 10/18 | |
| 第四周 | 1843/3426 | 2/5 | 10/28 | |
| 第五周 | 539/3965 | 2/7 | 20/48 | |
| 第六周 | 965/4936 | 1/8 | 20/68 | |
| 第七周 | 766/5702 | 1/9 | 20/88 | |
| 第八周 | 1562/7264 | 2/11 | 20/108 |
结对及互评
- 博客中值得学习的或问题:
排版精美,对于问题研究得很细致,解答也很周全。 - 代码中值得学习的或问题:
代码写的很规范,思路很清晰,继续加油!
点评过的同学博客和代码
结对学习内容
- 第十二章 堆