学号 20172326 《程序设计与数据结构》第七周学习总结
教材学习内容总结
AVL树
-
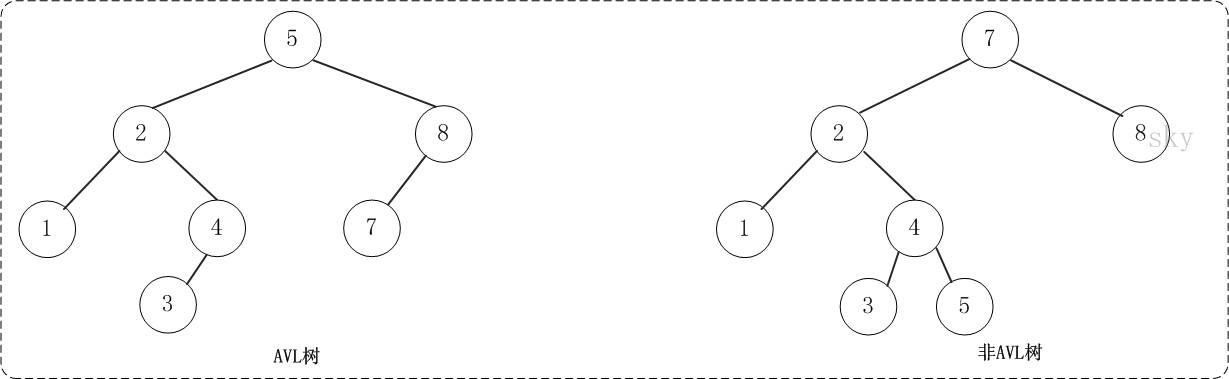
AVL树是实现平衡二叉树的一种算法实现,别的方法也可实现例如红黑树。
-
-
平衡因子:右子树高度-左子树高度的差值(高度是指当前结点到叶子结点的最长路径,如所有叶子结点的高度都为0,而深度则是指从根结点到当前结点的最大路径,如根结点的深度为0。),规定AVL树的平衡因子不大于1。所以在一个已经实现的AVL树中,任意一个节点的平衡因子的取值为(1,-1,0)。
-
左旋,右旋,左右旋,右左旋。当进行插入抑或是删除操作时,可能导致一个平衡二叉树失衡,因此就要对其进行调整,使其恢复平衡。可以简单的用列表遍历这个数,重新构造一个新的树,但这种方法太过简单,粗暴。所以我们可以使用旋转树,来使其恢复平衡。以下是几种失衡的AVL树。
-

-

-
右旋(或称为左左旋),经过计算,发现某一失衡点的左子树的深度大于右子树,这时就需要将左子树向“右”旋转,使其恢复平衡。方法:将失衡点的左结点设为当前树的新根,使原根变为新根的右结点,将新根的右结点变为原根的左结点。
-
左旋,失衡点处右子树的深度大于左子树,将右子树向左旋转。原理与右旋对称。
-
当某一子树太深时,仅通过一次右旋或左旋将无法完成,因此,我们需要使用两次旋转来实现它。因为旋转方法总是对称的,所以,只拿左右旋转为例。
-
左右旋,当左孩子的右子树太深时,进行旋转。先将其父节点变为其左孩子,同时将其左左孩子进行分配。
-
在执行结束操作后,通过比较每个结点的平衡因子来维持AVL树的平衡
红黑树
-
根结点为黑色;每个结点只有红色或黑色;所有的叶结点为黑色;红结点的孩子均为黑色;对于每个结点,从该结点到其叶子结点构成的所有路径上的黑结点个数相同;
-
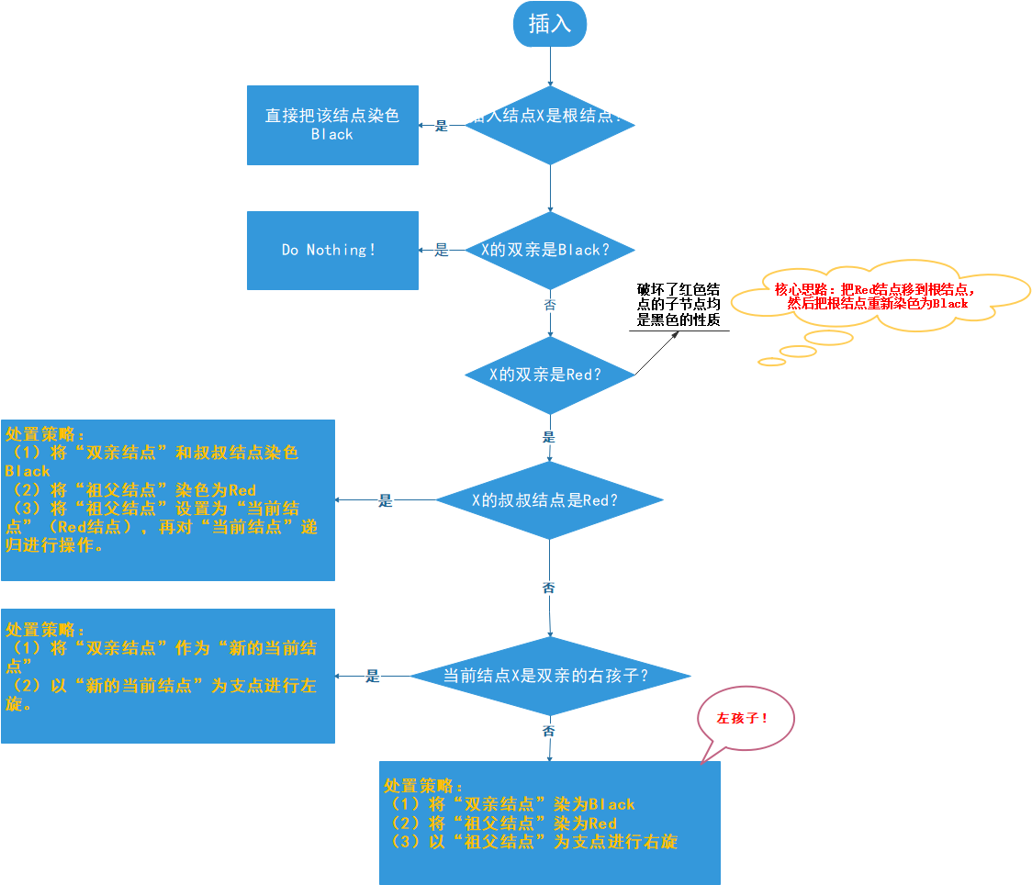
插入结点。1.插入结点为对应的根结点,直接将其涂黑即可。2.插入结点的父节点为黑结点,那么,直接插入即可。3.插入的父节点为红色。此时将破坏红黑树的结构,因此需要将其进行旋转。 分为以下三种情况,满足之一的条件时,进行递归。
-
- 当插入结点的父结点为红,且叔结点也为红时,将其父结点与叔结点改为红色,祖父结点变为黑色。并将带操作结点改为祖父结点
-
- 当待操作结点的父节点是红色的,叔叔节点是黑色的,且插入节点是其父节点的右子节点。这时,将待操作结点改为其父结点,再将带操作结点左旋。
-
- 待操作结点的父结点是红色,叔叔结点是黑色,且插入结点是其父结点的左子结点。我们要做的操作有:将当前结点的父结点涂黑,将祖父结点涂红,在祖父结点为支点做右旋操作。最后把根结点涂黑,整个红-黑树重新恢复了平衡。
-

-
-
删除操作:
-
- 第一步:将红黑树当作一颗二叉查找树,将节点删除。
这和"删除常规二叉查找树中删除节点的方法是一样的"。分3种情况:
① 被删除节点没有儿子,即为叶节点。那么,直接将该节点删除就OK了。
② 被删除节点只有一个儿子。那么,直接删除该节点,并用该节点的唯一子节点顶替它的位置。
③ 被删除节点有两个儿子。那么,先找出它的后继节点;然后把“它的后继节点的内容”复制给“该节点的内容”;之后,删除“它的后继节点”。在这里,后继节点相当于替身,在将后继节点的内容复制给"被删除节点"之后,再将后继节点删除。这样就巧妙的将问题转换为"删除后继节点"的情况了,下面就考虑后继节点。 在"被删除节点"有两个非空子节点的情况下,它的后继节点不可能是双子非空。既然"的后继节点"不可能双子都非空,就意味着"该节点的后继节点"要么没有儿子,要么只有一个儿子。若没有儿子,则按"情况① "进行处理;若只有一个儿子,则按"情况② "进行处理。
- 第一步:将红黑树当作一颗二叉查找树,将节点删除。
-
- 第二步:通过"旋转和重新着色"等一系列来修正该树,使之重新成为一棵红黑树。
因为"第一步"中删除节点之后,可能会违背红黑树的特性。所以需要通过"旋转和重新着色"来修正该树,使之重新成为一棵红黑树。
- 第二步:通过"旋转和重新着色"等一系列来修正该树,使之重新成为一棵红黑树。
-

教材学习中的问题和解决过程
- 问题1:
Comparable<T> comparableElement = (Comparable<T>)element
为什么要使用comparable来将element转为相关格式呢?
-
问题1理解:这是添加元素方法(addElement)的一部分代码,将传入的参数转化为comparable型。为什么不在传入的时候直接将其变为comparable类型呢?况且直接变为comparable型数据,在之后的维护平衡树时有助于进行插入元素之间的比较。我们知道,在方法中传入一个comparable参数看似简单,但在真正通过输入数据的时候,可能是一个string值,也可能是一个int值,但是,想传入一个comparable类型数据,基本不可能,所以,选择了在方法中进行类型转化。
-
问题2:红黑树的平衡问题
-
问题2理解:首先,我们知道,红黑树通过颜色来控制平衡。尤其是黑色结点,通过每条路径有相同数目的黑色结点。同时,每个红色结点的孩子结点为黑色。可以想象,想沿着一边子树的一个方向插入众多的结点将不可实现,从而实现了平衡。同时,根据二叉查找树的性质可知,若删除一个结点,除非该结点为根结点且为红色,否则必需经过一些操作以维持平衡。
-
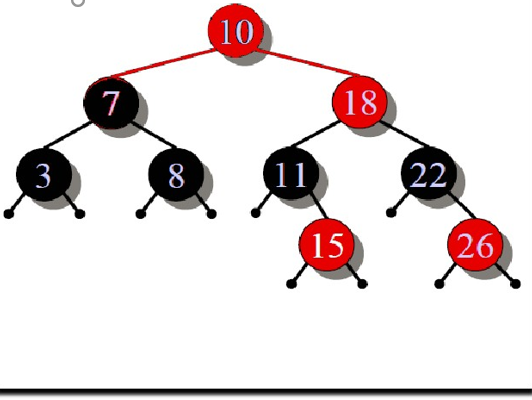
在课堂上,大家发现了一个问题。这种时候,应该怎样操作,对于结点(7)结点(8),无论将其变为黑色还是红色,都符合要求。那么,为什么还要将其涂为红色呢?
-
-
涂为红色,有什么变化呢?相较于涂为黑色,黑色结点减少,且其孩子结点为黑色。如果是黑色呢?该树整体黑色结点增多。但问题恰恰就在这里,如果这是一颗单独的树还好说,但如果是某一棵树的子树呢?只有这一部分的黑色结点增加,别的均不变,这直接导致违反了规定。所以,从中也可以看出,对于红黑树,黑色结点的变化是相当慎重的。从规定插入的结点默认为红色也可以看出这点。
代码问题
- 问题1:AVL树实现动态平衡的方法
- 理解:当顺序输入一组数据“1 2 3 4 5 6 7 8 9”时,如果没有相应的平衡方法,就会出现这种情况。

- 这种情况之前博客也曾提到,是平衡二叉树决不能出现的情况,那么,应该如何处理呢?从思路分析,我们必须要更换根结点的元素,也就是说当一组数据顺序进入时,一旦违反平衡因子的大小,立刻对树中的元素进行对比,将能够平衡树的根找出来,类似于将之前的树折成两半。理想的效果是这样的,也就是说,平衡是动态的,随时根据平衡因子的大小来调整树的元素分布。

因此,一开始,我的思路是,通过比较所有元素来确定一个中间大小的数据来作为根。可是,这一实现过程较为麻烦,需要将当前树进行重构。翻了翻书,看到大篇幅的旋转,我就知道应该怎样做了。可以看到,每次旋转,都是由部分到整体,从某一棵失衡的子树开始,再向上旋转,再判断再旋转。所以,这是一个重复的过程,因此,可以用递归实现。代码将较为简单。
if (data.compareTo(p.getElement()) < 0) {//向左子树寻找插入位置
p.setLeft(insert(data, p.getLeft()));
if (height(p.getLeft()) - height(p.getRight()) == 2) {//插入后计算子树的高度,等于2则需要重新恢复平衡,由于是左边插入,左子树的高度肯定大于等于右子树的高度
//判断data是插入点的左孩子还是右孩子
if (data.compareTo(p.getLeft().getElement()) < 0) {
//进行LL旋转
p = singleRotateLeft(p);
} else {
//进行左右旋转
p = doubleRotateWithLeft(p);
}
}
}
这里是部分代码,全部的有点长,就不进行展示。这里最为关键的就是这行代码“ p.setLeft(insert(data, p.getLeft()));
”也就是重复利用递归的部分,通过代替循环体,我们直接锁定需要插入的位置,在插入结束后,直接就插入结点的父结点的平衡因子来判断插入是否导致失衡,也就是与2进行判断,如果违规,直接进行旋转。这样一来,在树的底层位置进行旋转,尽可能缩小涉及到的范围,也就使得更加便于实现。
代码托管
其他(感悟、思考等,可选)
- 本章的知识不好理解,尤其是红黑树,涉及了大量的不同情况,令人头秃,而且网上的知识有漏洞的也很多,继续自己体会。
学习进度条
| 代码行数(新增/累积) | 博客量(新增/累积) | 学习时间(新增/累积) | 重要成长 | |
|---|---|---|---|---|
| 目标 | 5000行 | 30篇 | 400小时 | |
| 第一周 | 0/0 | 1/1 | 3/3 | |
| 第二周 | 409/409 | 1/2 | 5/8 | |
| 第三周 | 1174/1583 | 1/3 | 10/18 | |
| 第四周 | 1843/3426 | 2/5 | 10/28 | |
| 第五周 | 539/3965 | 2/7 | 20/48 | |
| 第六周 | 965/4936 | 1/8 | 20/68 | |
| 第七周 | 766/5702 | 1/9 | 20/88 |
结对及互评
- 博客中值得学习的或问题:
排版精美,对于问题研究得很细致,解答也很周全。 - 代码中值得学习的或问题:
代码写的很规范,思路很清晰,继续加油!
点评过的同学博客和代码
结对学习内容
- 第十一章 二叉查找树