Codeforces Round #783 (Div. 2)

Codeforces Round #783 (Div. 2)

A - Direction Change

保证让\(n \geq m\), 只要\(m > 1\) 在第二维上就可以反复横跳，则必定有解

int main() {
    IOS;
    for (cin >> _; _; --_) {
        cin >> n >> m;
        if (m > n) swap(n, m);
        if (n - m > 1 && m < 2) cout << -1 << '\n';
        else if (n - m < 2) cout << n + m - 2 << '\n';
        else if (n - m & 1) cout << 2 * n - 3 << '\n';
        else cout << 2 * n - 2 << '\n';
    }
    return 0;
}

B - Social Distance

先拆环

假设最后一个人坐在最后一个位置，则第一人必定坐在\(max(a_n, a_1) + 1\)的位置上，这样才能保证两人在换上相隔人数合法，

之后下一个人的位置\(s_i = s_{i - 1} + max(a_{i -1}, a_i) + 1\)，只要保证最后一个人位置不超过拆环的序列长度即可，

假定$a_0 = a_n, b_i = max(a_{i - 1}, a_i) $

然后就是贪心，使得两人之间所需空位差距尽量最小，排个序即可

int main() {
    IOS;
    for (cin >> _; _; --_) {
        cin >> n >> m;
        bool f = 1;
        for (int i = 1; i <= n; ++i) cin >> a[i];
        sort(a + 1, a + 1 + n);
        a[0] = a[n];
        for (int i = 1; i <= n; ++i) b[i] = max(a[i], a[i - 1]);
        for (int i = 1, j = 0; i <= n && f; ++i) {
            j += b[i] + 1;
            if (j > m) f = 0;
        }
        cout << (f ? "YES" : "NO") << '\n';
    }
    return 0;
}

C - Make it Increasing

模拟题意暴力即可，必定存在一个位置\(i\)不用操作，且其前面的数都要进行 减 操作，其后面的数都需要 加 操作，

暴力去枚举这个\(i\)即可

int main() {
    IOS;
    cin >> n;
    for (int i = 1; i <= n; ++i) cin >> a[i];
    long long mx = 2e18;
    for (int i = 1; i <= n; ++i) {
        long long cur = 0, ls = 0;
        for (int j = i - 1; j; --j) {
            long long c = ls / a[j] + 1;
            cur += c; ls = a[j] * c;  
        }
        ls = 0;
        for (int j = i + 1; j <= n; ++j) {
            long long c = ls / a[j] + 1;
            cur += c; ls = a[j] * c;  
        }
        umin(mx, cur);
    }
    cout << mx;
    return 0;
}

D - Optimal Partition

dp, \(f_i\) 表示以\(i\)结尾分割后的最大值，则

\(f_i = \left\{\begin{matrix} max(f_j + i - j)& \sum_{k = 1}^i a_k > \sum_{k = 1}^j a_k\\ max(f_j) & \sum_{k = 1}^i a_k = \sum_{k = 1}^j a_k\\ max(f_j - i + j) & \sum_{k = 1}^i a_k < \sum_{k = 1}^j a_k \end{matrix}\right. \quad i > j \geq 0\)

即

\(\left\{\begin{matrix} f_i - i = max(f_j - j)& \sum_{k = 1}^i a_k > \sum_{k = 1}^j a_k\\ f_i = max(f_j) & \sum_{k = 1}^i a_k = \sum_{k = 1}^j a_k\\ f_i + i= max(f_j + j) & \sum_{k = 1}^i a_k < \sum_{k = 1}^j a_k \end{matrix}\right. \quad i > j \geq 0\)

一维偏序用for循环搞定，对于前缀和的偏序可以通过数轴映射，离散化在数轴上表示前缀和

再随便找数据结构维护数轴上的 \(f_i - i, f_i, f_i + i\) 的区间最值信息即可

本人选择线段树，一棵即能维护这三种信息在区间最值的信息

const int N = 5e5 + 5;
 
struct BIT {
    struct node {
        int l, r, val[3];
    } tr[N << 2];
    void build(int p, int l, int r) {
        tr[p] = {l, r, {-1000000, -1000000, -1000000}};
        if (l == r) return;
        int mid = l + r >> 1;
        build(p << 1, l, mid); build(p << 1 | 1, mid + 1, r);
    }
    void change(int p, int k, int v, int id) {
        if (tr[p].l == k && tr[p].r == k) {
            umax(tr[p].val[0], v - id);
            umax(tr[p].val[1], v);
            umax(tr[p].val[2], v + id);
            return;
        }
        int mid = tr[p].l + tr[p].r >> 1;
        if (mid >= k) change(p << 1, k, v, id);
        else change(p << 1 | 1, k, v, id);
        rep(i, 0, 2) umax(tr[p].val[i], max(tr[p << 1].val[i], tr[p << 1 | 1].val[i]));
    }
    int ask(int p, int l, int r, int k) {
        if (tr[p].l >= l && tr[p].r <= r) return tr[p].val[k];
        int mid = tr[p].l + tr[p].r >> 1;
        if (mid >= r) return ask(p << 1, l, r, k);
        else if (mid < l) return ask(p << 1 | 1, l, r, k);
        return max(ask(p << 1, l, r, k), ask(p << 1 | 1, l, r, k));
    }
} bit;
 
int n, m, _, k, cas;
long long a[N], b[N];
 
int main() {
    IOS;
    for (cin >> _; _; --_) {
        cin >> n;
        vector<long long> c(1, 0);
        for (int i = 1; i <= n; ++i)
            cin >> a[i], c.emplace_back(a[i] += a[i - 1]); 
        sort(all(c)); c.erase(unique(all(c)), c.end());
        m = c.size();
        for (int i = 1; i <= n; ++i) b[i] = lower_bound(all(c), a[i]) - c.begin() + 1;
        bit.build(1, 1, m);
 
        int cur;
        bit.change(1, lower_bound(all(c), 0) - c.begin() + 1, 0, 0);
        for (int i = 1, ls = 0; i <= n; ++i, ls = cur) {
            cur = (a[i] - a[i - 1] > 0 ? 1 : a[i] - a[i - 1] < 0 ? -1 : 0) + ls;
            long long t = bit.ask(1, b[i], b[i], 1);
            umax(cur, bit.ask(1, b[i], b[i], 1));
            if (b[i] > 1) umax(cur, bit.ask(1, 1, b[i] - 1, 0) + i);
            if (b[i] < m) umax(cur, bit.ask(1, b[i] + 1, m, 2) - i);
            bit.change(1, b[i], cur, i);
        }
        cout << cur << '\n';
    }
    return 0;
}

E - Half Queen Cover

不考虑斜着。则就是\(n\)个半皇后占据\(n\)行\(n\)列，考虑斜着，也就是\(k\)个半皇后形成的对角线正好拼成了一g个\((n - k) \times (n - k)\)的矩形

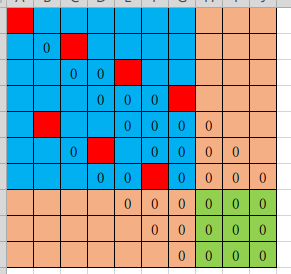
如图，\(k = 7\) 半皇后用行列覆盖了\(k \times k\)矩形，并额外还覆盖到了肉色的两个矩形，并通过\(n - k\)条对角线覆盖了\((n - k) \times (n - k)\)的矩形

边长为\(n - k\)的正方形有\((n - k) * 2 - 1\) 条对角线，则 \(k \geq 2 \times n - 2 \times k - 1\)

则 \(k = \left \lceil \frac{2n - 1}{3} \right \rceil\), 之后就是构造\(k\)个半皇后覆盖\(k * k\)矩形的问题

int main() {
    IOS;
    cin >> n; m = (2 * n + 1) / 3;
    cout << m << '\n';
    for (int i = 1, j = 1; i <= m; ++i, j += 2) {
        if (j > m) j = 2;
        cout << i << ' ' << j << '\n';
    }
    return 0;
}