Codeforces Round #672 (Div. 2)

A

给定次数 n * (n - 1) /2 - 1, 像什么?

把后面的 减一 去掉, 不就是冒泡排序的上限吗?

那不就是只要 原数组不是单调递减需要 n * (n - 1) / 2 次交换, 其他的都可以吗?

#include <bits/stdc++.h>
#define all(n) (n).begin(), (n).end()
#define se second
#define fi first
#define pb push_back
#define mp make_pair
#define sqr(n) (n)*(n)
#define rep(i,a,b) for(int i=(a);i<=(b);++i)
#define per(i,a,b) for(int i=(a);i>=(b);--i)
#define IOS ios::sync_with_stdio(false);cin.tie(nullptr);cout.tie(nullptr)
using namespace std;
typedef unsigned long long ull;
typedef long long ll;
typedef unsigned long long ull;
typedef pair<int, int> PII;
typedef pair<ll, ll> PLL;
typedef vector<int> VI;
typedef double db;
 
const int N = 1e5 + 5;
 
int n, m, _, k;
int a[N] = {2100000000};
 
int main() {
    IOS;
    for (cin >> _; _; --_) {
        cin >> n; bool f = 1;
        rep (i, 1, n) {
            cin >> a[i];
            if (a[i] >= a[i - 1]) f = 0;
        }
        if (f) cout << "NO
";
        else cout << "YES
";
    }
    return 0;
}

B

只有最高位都是 1, a & b > a ^ b, 不然 a & b < a ^ b

直接统计最高位为 1 << i 的数量, 算一下就好了

#include <bits/stdc++.h>
#define all(n) (n).begin(), (n).end()
#define se second
#define fi first
#define pb push_back
#define mp make_pair
#define sqr(n) (n)*(n)
#define rep(i,a,b) for(int i=(a);i<=(b);++i)
#define per(i,a,b) for(int i=(a);i>=(b);--i)
#define IOS ios::sync_with_stdio(false);cin.tie(nullptr);cout.tie(nullptr)
using namespace std;
typedef unsigned long long ull;
typedef long long ll;
typedef unsigned long long ull;
typedef pair<int, int> PII;
typedef pair<ll, ll> PLL;
typedef vector<int> VI;
typedef double db;
 
const int N = 1e5 + 5;
 
int n, m, _, k;
ll a[N], b[32];
 
int main() {
    IOS;
    for (cin >> _; _; --_) {
        cin >> n;
        rep (i, 0, 30) b[i] = 0;
        rep (i, 1, n) {
            cin >> a[i];
            per (j, 30, 0)
                if ((a[i] >> j) & 1) { ++b[j]; break; }
        }
        ll ans = 0;
        rep (i, 0, 30) ans += (b[i] - 1) * b[i] >> 1;
        cout << ans << '
';
    }
    return 0;
}

C1 easy

不交换, 只要找到一对 a[i] - a[j] > 0 就塞进去

当然确保 a[i] - a[j] + a[x] - a[y] 中 a[j] 是 i + 1 ~ x - 1 中最小的

那我们就得到了 (a[b_1] - a[b_2] + ... + a[b_k] - 0) 至于最后一个为什么成了0, 看看代码很好实现

然后就是贪心的删除数了, (a[b_2] > a[b_3]) 那我们肯定删除这两个数, 使得数组成 (a[b_1] - b[b_4] + ... + a[b_k] - 0), O(n)就全部处理完了

#include <bits/stdc++.h>
#define all(n) (n).begin(), (n).end()
#define se second
#define fi first
#define pb push_back
#define mp make_pair
#define sqr(n) (n)*(n)
#define rep(i,a,b) for(int i=(a);i<=(b);++i)
#define per(i,a,b) for(int i=(a);i>=(b);--i)
#define IOS ios::sync_with_stdio(false);cin.tie(nullptr);cout.tie(nullptr)
using namespace std;
typedef unsigned long long ull;
typedef long long ll;
typedef unsigned long long ull;
typedef pair<int, int> PII;
typedef pair<ll, ll> PLL;
typedef vector<int> VI;
typedef double db;
 
const int N = 3e5 + 5;
 
int n, m, _, k;
ll a[N];
 
int main() {
    IOS;
    for (cin >> _; _; --_) {
        cin >> n >> m >> a[1];
        ll h = a[1], ans = 0;
        vector<ll> c;
        rep (i, 2, n) {
            cin >> a[i];
            if (h > a[i]) {
                c.pb(h); c.pb(a[i]); 
                ans += h - a[i]; h = 0;
            }
            else {
                if (!c.empty() && h && h < c.back()) ans += c.back() - h, c.back() = h; 
                h = a[i];
            }
        }
        c.pb(h), ans += h;
        for (int i = 2; i < c.size(); i += 2) if (c[i] - c[i - 1] < 0) ans += c[i - 1] - c[i];
        cout << ans << '
'; 
    }
    return 0;
}

C2 hard

好好想想, C1 easy的贪心策略, 是怎么贪心算出答案的?

给个图, 自己思考一下

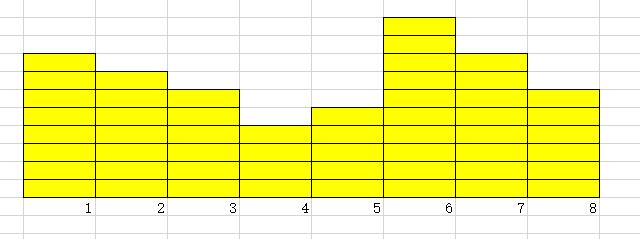
设 a[0] = a[n + 1] = 0

我们初次选定 a[1] - a[2] + a[3] - a[4] + a[6] - a[7] + a[8] - a[n + 1] (0)

根据我们的 (a[b_2] > a[b_3]) 的删除数, 得到 a[1] - a[4] + a[6], 看看我们选出来的数有什么特殊?

正数全是大于两边的, a[1] > max(a[0], a[2]), a[6] > max(a[5], a[7])

负数全是小于两边的 a[4] < max(a[3], a[5])

为什么呢? 在我们更新 h 的时候 也在更新减去的数, 在递减就会更新, 应该结合图很好理解, 剩下的就好做了

#define all(n) (n).begin(), (n).end()
#define se second
#define fi first
#define pb push_back
#define mp make_pair
#define sqr(n) (n)*(n)
#define rep(i,a,b) for(int i=(a);i<=(b);++i)
#define per(i,a,b) for(int i=(a);i>=(b);--i)
#define IOS ios::sync_with_stdio(false);cin.tie(nullptr);cout.tie(nullptr)
using namespace std;
typedef unsigned long long ull;
typedef long long ll;
typedef unsigned long long ull;
typedef pair<int, int> PII;
typedef pair<ll, ll> PLL;
typedef vector<int> VI;
typedef double db;
 
const int N = 3e5 + 5;
 
int n, m, _, k;
ll a[N], ans;
 
void add(int x, int k) {
    if (a[x] > max(a[x - 1], a[x + 1])) ans += k * a[x];
    else if (a[x] < min(a[x - 1], a[x + 1])) ans -= k * a[x];
}

int main() {
    IOS;
    for (cin >> _; _; --_) {
        cin >> n >> m; a[n + 1] = ans = 0;
        rep (i, 1, n) cin >> a[i];
        rep (i ,1, n) add(i, 1);
        cout << ans << '
';
        rep (i, 1, m) {
            int l, r; cin >> l >> r;
            rep (i, -1, 1) {
                add(l + i, -1);
                if (r + i > l + 1) add(r + i, -1);
            }
            swap(a[l], a[r]);
            rep (i, -1, 1) {
                add(l + i, 1);
                if (r + i > l + 1) add(r + i, 1);
            }
            cout << ans << '
';
        }
    }
    return 0;
}

D

贪心, 按照灯的点亮时间排序, 组合数学一下就行, 看看代码就明白了

cf竟然不让数组下标为负数, 哭唧唧

#include <bits/stdc++.h>
#define all(n) (n).begin(), (n).end()
#define se second
#define fi first
#define pb push_back
#define mp make_pair
#define sqr(n) (n)*(n)
#define rep(i,a,b) for(int i=(a);i<=(b);++i)
#define per(i,a,b) for(int i=(a);i>=(b);--i)
#define IOS ios::sync_with_stdio(false);cin.tie(nullptr);cout.tie(nullptr)
using namespace std;
typedef unsigned long long ull;
typedef long long ll;
typedef unsigned long long ull;
typedef pair<int, int> PII;
typedef pair<ll, ll> PLL;
typedef vector<int> VI;
typedef double db;
 
const int N = 3e5 + 5, mod = 998244353;
 
int n, m, _, k;
PII a[N];
int t[N << 1], tot, in[N << 1], out[N << 1];
ll p[N], inv[N];
 
ll qpow(ll a, ll b) {
    ll ans = 1;
    for (; b; a = a * a % mod, b >>= 1)
        if (b & 1) ans = ans * a % mod;
    return ans;
}
 
void init(int n) {
    p[0] = 1; inv[0] = 1;
    for(int i = 1; i <= n; i++) {
        p[i] = p[i-1] * i % mod;
        inv[i] = inv[i-1] * qpow(i, mod - 2) % mod;
    }
}
 
int main() {
    IOS; cin >> n >> m; init(3e5);
    rep (i, 1, n) {
        cin >> a[i].fi >> a[i].se, t[++tot] = a[i].fi, t[++tot] = a[i].se;
    }
    sort(t + 1, t + 1 + tot);
    unordered_map<int ,int> st;
    tot = unique(t + 1, t + 1 + tot) - t - 1;
    rep (i, 1, tot) st[t[i]] = i;
    rep (i, 1, n) ++in[st[a[i].fi]], ++out[st[a[i].se]];
    ll ans = 0, cnt = 0;
    rep (i, 1, tot) {
        cnt += in[i];
        if (out[i] && cnt >= m)
            rep (j, max(1ll, m - cnt + out[i]), min(out[i], m))
                ans = (ans + p[out[i]] * inv[j] % mod * inv[out[i] - j] % mod * p[cnt - out[i]] % mod * inv[m - j] % mod * inv[cnt - out[i] - m + j] % mod) % mod;
        cnt -= out[i];
    }
    cout << ans;
    return 0;
}