题意
给定正多边形的边数为(2 * n, n为偶数), 求最小外接正方形的边长
题解
所以边数是其实是 4 * n, 就意味着这个多边形有四条边在正方形上
每次(n + 1)边数 +4, 就是把左上,左下,右上.右下的边扩展并调整边的长度
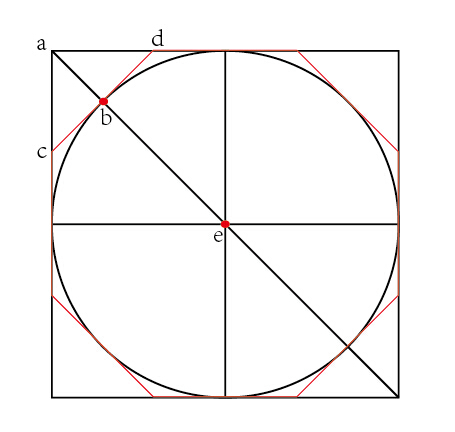
从(4边形到8边形, n = 1 ~ n = 2) 缩短在正方形边上的边, 并在左上,左下,右上.右下添加新的4条边
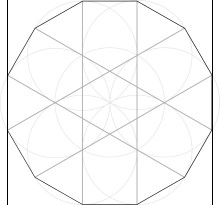
从(8边形到12边形, n = 2 ~ n = 3) 缩短在正方形边上的边, 并在左上,左下,右上.右下添加新的4条边
所以不论n多大, 都是类似的四条边在正方形上, 两条平行边的距离就是正方形的边长
而这是正多边形, 直接从中心作垂线, 直接算就行, L = (a / 2) / tan(360° / 边数) * 2
#include <bits/stdc++.h>
#define all(n) (n).begin(), (n).end()
#define se second
#define fi first
#define pb push_back
#define mp make_pair
#define sqr(n) (n)*(n)
#define rep(i,a,b) for(int i=a;i<=b;++i)
#define per(i,a,b) for(int i=a;i>=b;--i)
using namespace std;
typedef long long ll;
typedef pair<int, int> PII;
typedef vector<int> VI;
typedef double db;
const int N = 1e6 + 5;
int n, m, _, k;
int a[N];
int main()
{
//ios::sync_with_stdio(0); cin.tie(0);
double pi = 3.1415926535898;
for (cin >> _; _; --_)
{
cin >> n; n <<= 1;
printf("%.6lf
", (1.0 / tan(acos(-1) / n)));
}
return 0;
}