返回一个整数数组中最大子数组的和

　　要求： 输入一个整形数组，数组里有正数也有负数。 数组中连续的一个或多个整数组成一个子数组，每个子数组都有一个和。 求所有子数组的和的最大值。要求时间复杂度为O(n)

　　

#include<iostream>
using namespace std;
int main()
{
    int a[100];
    int i,n;
    int m=-1000000;
    cin>>n;

    for(i=0;i<n;i++)
        cin>>a[i];

    for(i=1;i<n;i++)
    {
        if(a[i]+a[i-1]>a[i])
            a[i]=a[i]+a[i-1];
    }

    for(i=0;i<n;i++)
        m=max(m,a[i]);
    cout<<m<<endl;
    return 0;
}

思路：

先将所有的数输入构成数组，然后采用赋值法，如果这个数小于前面所有数的和，那么这个数就赋值为前面的数的和，最后求得赋值之后的最大值。

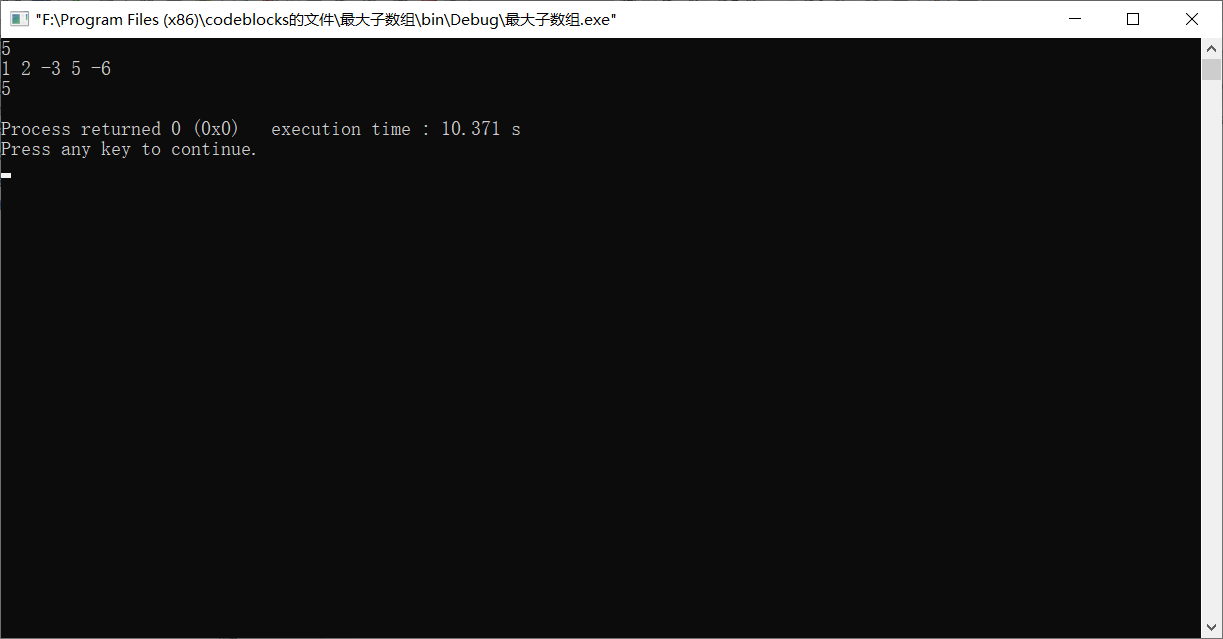
截图