11. 盛最多水的容器

给定 n 个非负整数 a1，a2，...，an，每个数代表坐标中的一个点 (i, ai) 。在坐标内画 n 条垂直线，垂直线 i 的两个端点分别为 (i, ai) 和 (i, 0)。找出其中的两条线，使得它们与 x 轴共同构成的容器可以容纳最多的水。

说明：你不能倾斜容器，且 n 的值至少为 2。

 

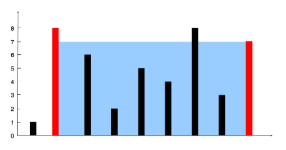
图中垂直线代表输入数组 [1,8,6,2,5,4,8,3,7]。在此情况下，容器能够容纳水（表示为蓝色部分）的最大值为 49。

示例:

输入: [1,8,6,2,5,4,8,3,7]
输出: 49

/*
解题思路：
这道只是让求最大的一个的装水量，
我们需要定义i和j两个指针分别指向数组的左右两端，
然后两个指针向中间搜索，每移动一次算一个值和结果比较取较大的，
容器装水量的算法是找出左右两个边缘中较小的那个乘以两边缘的距离
*/

#include<iostream>
#include<vector>
#include<algorithm>
using namespace std;
class Solution {
public:
	int maxArea(vector<int>& height)
	{
	
				int res = 0, i = 0, j = height.size() - 1;
				while (i < j) 
				{
					res = max(res, min(height[i], height[j]) * (j - i));
					height[i] < height[j] ? ++i : --j;
				}
				return res;
	 }
};

int main()
{
	vector<int> vec;
	int i;
	while (cin.get() != '
')
	{
		cin >> i;
		vec.push_back(i);
	}
	cout << Solution().maxArea(vec) << endl;
	system("pause");
	return 0;
}