题目的传送门
题目描述
Linux用户和OSX用户一定对软件包管理器不会陌生。通过软件包管理器,你可以通过一行命令安装某一个软件包,然后软件包管理器会帮助你从软件源下载软件包,同时自动解决所有的依赖(即下载安装这个软件包的安装所依赖的其它软件包),完成所有的配置。Debian/Ubuntu使用的apt-get,Fedora/CentOS使用的yum,以及OSX下可用的homebrew都是优秀的软件包管理器。
你决定设计你自己的软件包管理器。不可避免地,你要解决软件包之间的依赖问题。如果软件包A依赖软件包B,那么安装软件包A以前,必须先安装软件包B。同时,如果想要卸载软件包B,则必须卸载软件包A。现在你已经获得了所有的软件包之间的依赖关系。而且,由于你之前的工作,除0号软件包以外,在你的管理器当中的软件包都会依赖一个且仅一个软件包,而0号软件包不依赖任何一个软件包。依赖关系不存在环(若有m(m≥2)个软件包A1,A2,A3,⋯,Am,其中A1依赖A2,A2依赖A3,A3依赖A4,……,A[m-1]依赖Am,而Am依赖A1,则称这m个软件包的依赖关系构成环),当然也不会有一个软件包依赖自己。
现在你要为你的软件包管理器写一个依赖解决程序。根据反馈,用户希望在安装和卸载某个软件包时,快速地知道这个操作实际上会改变多少个软件包的安装状态(即安装操作会安装多少个未安装的软件包,或卸载操作会卸载多少个已安装的软件包),你的任务就是实现这个部分。注意,安装一个已安装的软件包,或卸载一个未安装的软件包,都不会改变任何软件包的安装状态,即在此情况下,改变安装状态的软件包数为0。
输入输出格式
输入格式:
从文件manager.in中读入数据。
输入文件的第1行包含1个整数n,表示软件包的总数。软件包从0开始编号。
随后一行包含n−1个整数,相邻整数之间用单个空格隔开,分别表示1,2,3,⋯,n−2,n−1号软件包依赖的软件包的编号。
接下来一行包含1个整数q,表示询问的总数。之后q行,每行1个询问。询问分为两种:
install x:表示安装软件包x
uninstall x:表示卸载软件包x
你需要维护每个软件包的安装状态,一开始所有的软件包都处于未安装状态。
对于每个操作,你需要输出这步操作会改变多少个软件包的安装状态,随后应用这个操作(即改变你维护的安装状态)。
输出格式:
输出到文件manager.out中。
输出文件包括q行。
输出文件的第i行输出1个整数,为第i步操作中改变安装状态的软件包数。
输入输出样例
7
0 0 0 1 1 5
5
install 5
install 6
uninstall 1
install 4
uninstall 0
3
1
3
2
3
10
0 1 2 1 3 0 0 3 2
10
install 0
install 3
uninstall 2
install 7
install 5
install 9
uninstall 9
install 4
install 1
install 9
1
3
2
1
3
1
1
1
0
1
说明
【样例说明 1】
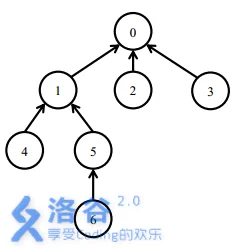
一开始所有的软件包都处于未安装状态。
安装5号软件包,需要安装0,1,5三个软件包。
之后安装6号软件包,只需要安装6号软件包。此时安装了0,1,5,6四个软件包。
卸载1号软件包需要卸载1,5,6三个软件包。此时只有0号软件包还处于安装状态。
之后安装4号软件包,需要安装1,4两个软件包。此时0,1,4处在安装状态。最后,卸载0号软件包会卸载所有的软件包。`
【数据范围】
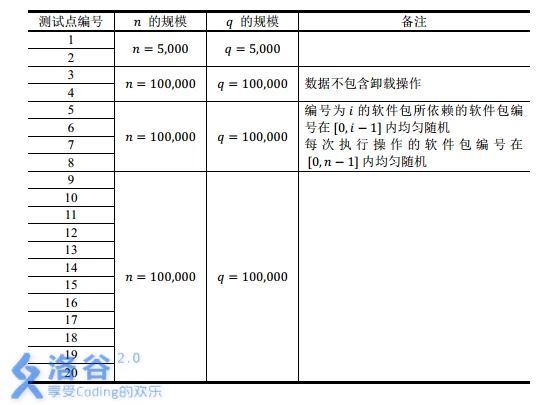
思路:
这题最难的应该在读题,一遍题目读下来都不知道在说什么。。。。
对于本题,有两个操作:
- install x :表示要安装软件包x;
- uninstall x :表示要卸载此安装包;
对于操作一,可以统计从x节点到根节点还未安装软件包的节点数,然后用区间改改成已安装。
对于操作二,可以先统计x所在的子树中已安装的节点数,然后将子树改为没安装。
其他的真的没什么,跟板子也没什么区别,只是注意别超时了,就像我原来的DFS1就写丑了,然后一堆T
1 #include<iostream>
2 #include<cstdio>
3 #include<cstdlib>
4 #include<algorithm>
5 #include<cstring>
6
7 using namespace std;
8
9 const int maxn=5e6+10;
10 struct node
11 {
12 int to,next;
13 }way[maxn];
14 struct tttt
15 {
16 int l,r,ls,rs;
17 int sum;
18 int lazy;
19 }tree[maxn];
20 int top[maxn];
21 int head[maxn];
22 int deep[maxn];
23 int size[maxn];
24 int dfsx[maxn];
25 int rt[maxn];
26 int n,m,rt1;
27 int son[maxn];
28 int tot;
29 int father[maxn];
30
31 int read()
32 {
33 int x=0;char ch=getchar();
34 while(ch<'0'||ch>'9'){ch=getchar();}
35 while(ch>='0'&&ch<='9'){x=(x<<1)+(x<<3)+ch-'0';ch=getchar();}
36 return x;
37 }
38
39 void add(int x,int y)
40 {
41 way[++tot].next=head[x];
42 way[tot].to=y;
43 head[x]=tot;
44 }
45
46 int len(int x)
47 {
48 return tree[x].r-tree[x].l+1;
49 }
50
51 /*void dfs1(int x)
52 {
53 deep[x]=deep[father[x]]+1;
54 size[x]=1;
55 for(int i=head[x];i;i=way[i].next)
56 {
57 int to=way[i].to;
58 if(to!=father[x])
59 {
60 father[to]=x;
61 dfs1(to);
62 size[x]+=size[to];
63 if(size[to]>size[son[x]])
64 {
65 son[x]=to;
66 }
67 }
68 }
69 }*/
70
71 void dfs1(int u,int fa,int depth)
72 {
73 father[u]=fa;
74 deep[u]=depth;
75 size[u]=1;
76 for(int i=head[u];i;i=way[i].next)
77 {
78 int to=way[i].to;
79 if(to==fa)
80 continue;
81 dfs1(to,u,depth+1);
82 size[u]+=size[to];
83 if(size[to]>size[son[u]]||!son[u])
84 son[u]=to;
85 }
86 }
87 int dfs2(int x,int t)
88 {
89 top[x]=t;
90 dfsx[x]=++tot;
91 rt[tot]=x;
92 if(son[x])
93 {
94 dfs2(son[x],t);
95 }
96 for(int i=head[x];i;i=way[i].next)
97 {
98 int to=way[i].to;
99 if(to!=father[x]&&to!=son[x])
100 {
101 dfs2(to,to);
102 }
103 }
104 }
105
106 int pushup(int x)
107 {
108 tree[x].sum=tree[tree[x].rs].sum+tree[tree[x].ls].sum;
109 tree[x].l=tree[tree[x].ls].l;
110 tree[x].r=tree[tree[x].rs].r;
111 }
112
113 void build (int l,int r,int x)
114 {
115 if(l==r)
116 {
117 tree[x].ls=tree[x].rs=tree[x].lazy=-1;
118 tree[x].l=tree[x].r=l;
119 return ;
120 }
121 int mid=(l+r)>>1;
122 tree[x].ls=tot++;
123 tree[x].rs=tot++;
124 build(l,mid,tree[x].ls);
125 build(mid+1,r,tree[x].rs);
126 pushup(x);
127 }
128
129 int pushdown(int x)
130 {
131 int ls=tree[x].ls;
132 int rs=tree[x].rs;
133 int lz=tree[x].lazy;
134 tree[ls].sum=lz*len(ls);
135 tree[rs].sum=lz*len(rs);
136 tree[ls].lazy=tree[x].lazy;
137 tree[rs].lazy=tree[x].lazy;
138 tree[x].lazy=-1;
139 }
140
141 void update(int l,int r,int c,int x)
142 {
143 if(tree[x].l>=l&&tree[x].r<=r)
144 {
145 tree[x].lazy=c;
146 tree[x].sum=c*len(x);
147 return ;
148 }
149 if(tree[x].lazy!=-1)
150 pushdown(x);
151 int mid=(tree[x].l+tree[x].r)>>1;
152 if(mid>=l)
153 {
154 update(l,r,c,tree[x].ls);
155 }
156 if(mid<r)
157 {
158 update(l,r,c,tree[x].rs);
159 }
160 pushup(x);
161 }
162
163 int qwery(int l,int r,int x)
164 {
165 if(tree[x].l>=l&&tree[x].r<=r)
166 {
167 return tree[x].sum;
168 }
169 if(tree[x].lazy!=-1)
170 {
171 pushdown(x);
172 }
173 int mid=(tree[x].l+tree[x].r)>>1;
174 int res=0;
175 if(mid>=l)
176 {
177 res+=qwery(l,r,tree[x].ls);
178 }
179 if(mid<r)
180 {
181 res+=qwery(l,r,tree[x].rs);
182 }
183 return res;
184 }
185
186 int ask(int x)
187 {
188 int ans=0;
189 while(top[x])
190 {
191 ans+=dfsx[x]-dfsx[top[x]]-qwery(dfsx[top[x]],dfsx[x],rt1)+1;
192 update(dfsx[top[x]],dfsx[x],1,rt1);
193 x=father[top[x]];
194 }
195 ans+=dfsx[x]-dfsx[0]-qwery(dfsx[0],dfsx[x],rt1)+1;
196 update(dfsx[0],dfsx[x],1,rt1);
197 return ans;
198 }
199
200 int main()
201 {
202 n=read();
203 for(int i=1;i<n;i++)
204 {
205 int x;
206 x=read();
207 add(x,i);
208 add(i,x);
209 }
210 tot=0;
211 dfs1(0,-1,1);
212 dfs2(0,0);
213 tot=0;
214 rt1=tot++;
215 build(1,n,rt1);
216 m=read();
217 for(int i=1;i<=m;i++)
218 {
219 string flag;
220 cin>>flag;
221 int op;
222 op=read();
223 if(flag=="install")
224 {
225 printf("%d
",ask(op));
226 }
227 else
228 if(flag=="uninstall")
229 {
230 int ans=qwery(dfsx[op],dfsx[op]+size[op]-1,rt1);
231 printf("%d
",ans);
232 update(dfsx[op],dfsx[op]+size[op]-1,0,rt1);
233 }
234 }
235 return 0;
236 }