数论——类欧几里得算法

引入

解决

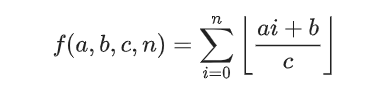
用O(logn)的算法求f(a,b,c,n)。

这个式子和我们以前见过的式子都长得不太一样。带向下取整的式子容易让人想到数论分块，然而数论分块似乎不适用于这个求和。但是我们是可以做一些预处理的。

如果说 a>=c或者b>=c，意味着可以将a,b对c取模以简化问题：

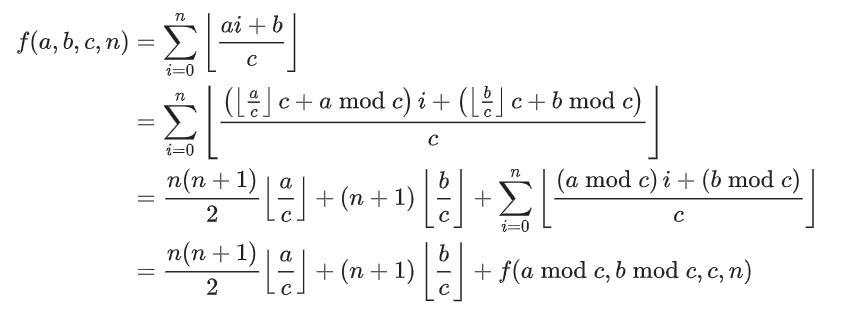
 问题又回到了a<c&&b<c的情况，而且该式子的条件为i<n，贡献为floor((a*i+b)/c),此时我们可以 将贡献与条件做转化,把贡献变成条件形成一个新式子：

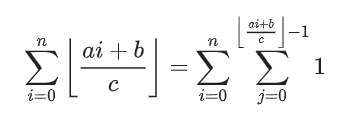
 现在多了个变量j，既然i的贡献不好求，那我们可以去求j的贡献，此时我们将该式限制转移，在上面的和式中n限制i的上界，而i限制j的上界。为了搞 j ，就先把 j 放到贡献的式子里,强制用n 限制j的上界

 将j<floor((a*i+b)/c)进行化简得出

这是一个递归的式子。并且你发现a,c分子分母换了位置，又可以重复上述过程。先取模，再递归。这就是一个辗转相除的过程，这也是类欧几里德算法的得名。

容易发现时间复杂度为 O(log(n))。

扩展

求

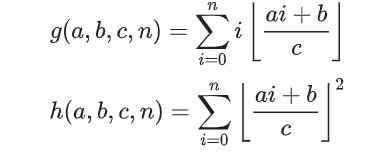
 对于g函数

和前面一样，进行取模，因为∑i*i=(n+1)*(2*n+1)*n/6,所以有

 

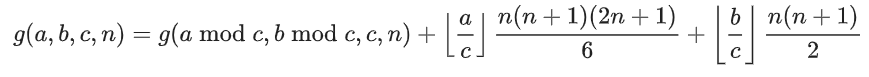
 对于h函数

同样先取模

 

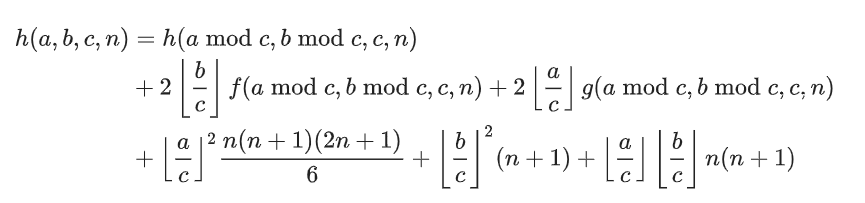
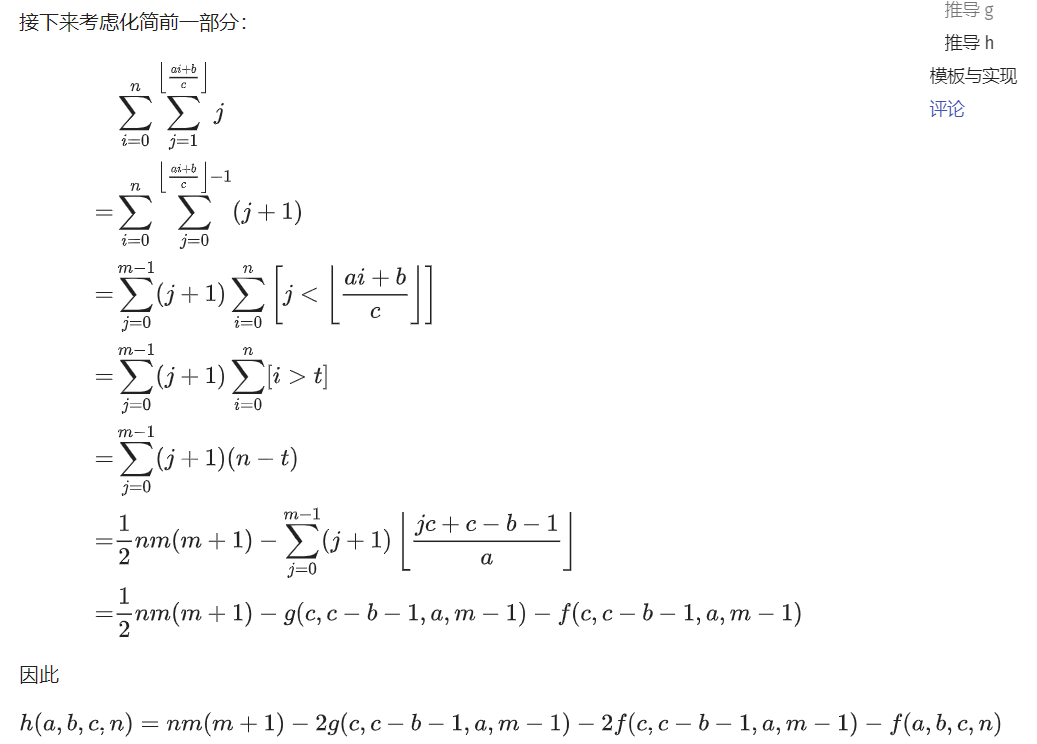
 因为三个函数交叉，所以模板是一起求出

#include <bits/stdc++.h>
#define int long long
using namespace std;
const int P = 998244353;
int i2 = 499122177, i6 = 166374059;
struct data {
  data() { f = g = h = 0; }
  int f, g, h;
};  // 三个函数打包
data calc(int n, int a, int b, int c) {
  int ac = a / c, bc = b / c, m = (a * n + b) / c, n1 = n + 1, n21 = n * 2 + 1;
  data d;
  if (a == 0)  // 迭代到最底层
  {
    d.f = bc * n1 % P;
    d.g = bc * n % P * n1 % P * i2 % P;
    d.h = bc * bc % P * n1 % P;
    return d;
  }
  if (a >= c || b >= c)  // 取模
  {
    d.f = n * n1 % P * i2 % P * ac % P + bc * n1 % P;
    d.g = ac * n % P * n1 % P * n21 % P * i6 % P + bc * n % P * n1 % P * i2 % P;
    d.h = ac * ac % P * n % P * n1 % P * n21 % P * i6 % P +
          bc * bc % P * n1 % P + ac * bc % P * n % P * n1 % P;
    d.f %= P, d.g %= P, d.h %= P;

    data e = calc(n, a % c, b % c, c);  // 迭代

    d.h += e.h + 2 * bc % P * e.f % P + 2 * ac % P * e.g % P;
    d.g += e.g, d.f += e.f;
    d.f %= P, d.g %= P, d.h %= P;
    return d;
  }
  data e = calc(m - 1, c, c - b - 1, a);
  d.f = n * m % P - e.f, d.f = (d.f % P + P) % P;
  d.g = m * n % P * n1 % P - e.h - e.f, d.g = (d.g * i2 % P + P) % P;
  d.h = n * m % P * (m + 1) % P - 2 * e.g - 2 * e.f - d.f;
  d.h = (d.h % P + P) % P;
  return d;
}
int T, n, a, b, c;
signed main() {
  scanf("%lld", &T);
  while (T--) {
    scanf("%lld%lld%lld%lld", &n, &a, &b, &c);
    data ans = calc(n, a, b, c);
    printf("%lld %lld %lld
", ans.f, ans.h, ans.g);
  }
  return 0;
}

 这次主要学习了贡献转条件求和方法，以及n的平方的一步化简，还有三个模板的运用。