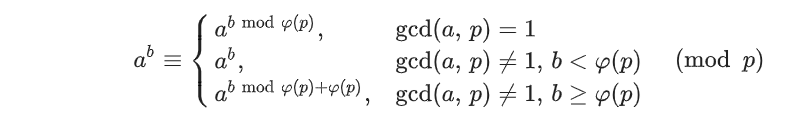数论——欧拉函数

欧拉函数

φ(n)表示的是小于等于 n和n 互质的数的个数，比如φ(1)=1。

很显然，当n为质数时φ(n)=n-1。

利用唯一分解定理，我们可以把一个整数唯一地分解为质数幂次的乘积，

 

 欧拉函数的一些性质：

1.欧拉函数是积性函数。

积性是什么意思呢？如果有 gcd(a,b)=1，那么 φ(a*b)=φ(a)*φ(b)。

特别地，当 n是奇数时 φ(2n)=φ(n)*φ(2)=φ(n)。

2.n=∑_d|nφ(d)

 3.若n=pk，其中p为质数，那φ(n)=pk-p^k-1(根据定义可得)

如何求欧拉函数

int euler_phi(int n) {
  int m = int(sqrt(n + 0.5));
  int ans = n;
  for (int i = 2; i <= m; i++)
    if (n % i == 0) {
      ans = ans / i * (i - 1);
      while (n % i == 0) n /= i;
    }
  if (n > 1) ans = ans / n * (n - 1);
  return ans;
}

如果求多个欧拉函数用线性筛法。

欧拉定理

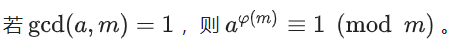
 扩展欧拉定理