贴现值计算

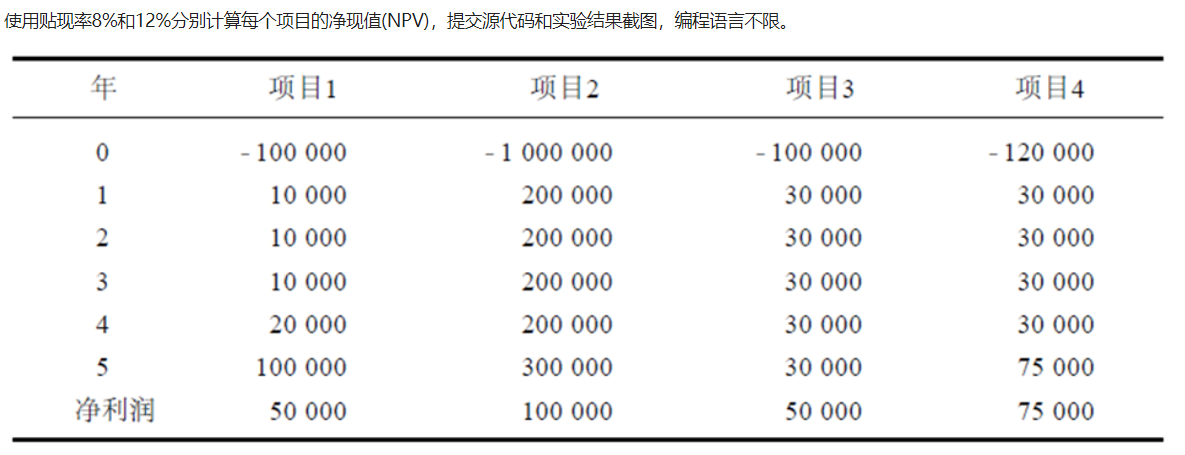
 代码：

package tiexian;
public class Tiexian {
	static int[] P1= new int[]{-100,10,10,10,20,100};
	static int[] P2= new int[]{-1000,200,200,200,200,300};
	static int[] P3= new int[]{-100,30,30,30,30,30};
	static int[] P4= new int[]{-120,30,30,30,30,75};
	public static double[] T=new double[6]; 
	public static void tiexianlv1() {
		double txp1=0;
		double txp2=0;
		double txp3=0;
		double txp4=0;
		double txl=1.08;
		for(int i=0;i<=5;i++)
		{
			T[i]=1/Math.pow(txl, i);
			System.out.println("当贴现率为8%时，第"+i+"年，贴现率为:"+T[i]);
		}
		for(int i=1;i<=5;i++) {
			txp1+=P1[i]*T[i];
			txp2+=P2[i]*T[i];
			txp3+=P3[i]*T[i];
			txp4+=P4[i]*T[i];
		}
		System.out.println("---------------------------------------");
		txp1=(txp1+P1[0])*1000;
		System.out.println("当贴现率为8%时，项目1的净现值为:"+txp1);
		txp2=(txp2+P2[0])*1000;
		System.out.println("当贴现率为8%时，项目2的净现值为:"+txp2);
		txp3=(txp3+P3[0])*1000;
		System.out.println("当贴现率为8%时，项目3的净现值为:"+txp3);
		txp4=(txp4+P4[0])*1000;
		System.out.println("当贴现率为8%时，项目4的净现值为:"+txp4);
		System.out.println("---------------------------------------");
		System.out.println("");
		System.out.println("---------------------------------------");
		
	}
	public static void tiexianlv2() {
		double txp1=0;
		double txp2=0;
		double txp3=0;
		double txp4=0;
		double txl=1.12;
		for(int i=0;i<=5;i++)
		{
			T[i]=1/Math.pow(txl, i);
			System.out.println("当贴现率为12%时，第"+i+"年，贴现率为:"+T[i]);
		}
		for(int i=1;i<=5;i++) {
			txp1+=P1[i]*T[i];
			txp2+=P2[i]*T[i];
			txp3+=P3[i]*T[i];
			txp4+=P4[i]*T[i];
		}
		System.out.println("---------------------------------------");
		txp1=(txp1+P1[0])*1000;
		System.out.println("当贴现率为12%时，项目1的净现值为:"+txp1);
		txp2=(txp2+P2[0])*1000;
		System.out.println("当贴现率为12%时，项目2的净现值为:"+txp2);
		txp3=(txp3+P3[0])*1000;
		System.out.println("当贴现率为12%时，项目3的净现值为:"+txp3);
		txp4=(txp4+P4[0])*1000;
		System.out.println("当贴现率为12%时，项目4的净现值为:"+txp4);
	}
	public static void main(String[] args) {
		tiexianlv1();
		tiexianlv2();	
	}

}

　　

最终结果：

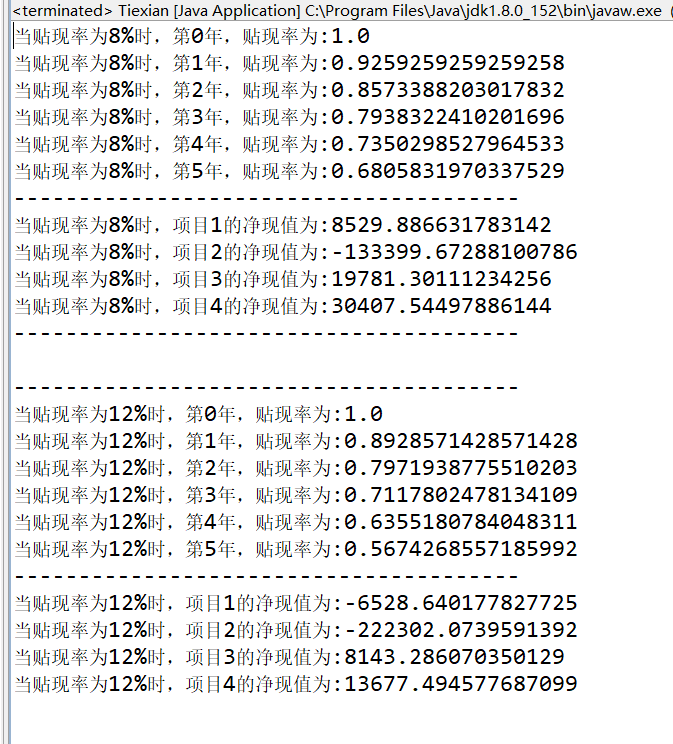
感触对比：

相较于纯利润和投资回报率两种方式。

因为纯利润没有考虑到项目的投入成本和现金流的时限，投资回报率没有考虑到现金时限和利率、利息。

而贴现现金流的恰好考虑到了前两种方法的缺陷之处，所以贴现现金流技术可以提供更好的项目选择标准。