格林(Green)公式告诉我们,在平面闭区域D上的二重积分可以通过沿闭区域D的边界曲线L上的曲线积分来表达。即,设闭区域$D$由分段光滑的曲线$L$围成,函数$P(x,y)$及$Q(x,y)$在$D$上具有一阶连续偏导数,则有$$\iint_{D}(\frac{\partial Q}{\partial x}-\frac{\partial P}{\partial y})dxdy=\oint_{L}Pdx+Qdy$$其中$L$是$D$的取正向的边界曲线。根据公式推导过程(参考高等数学同济版下),有如下关系存在:$$-\iint_{D}\frac{\partial P}{\partial y}dxdy=\oint_{L}Pdx\\\iint_{D}\frac{\partial Q}{\partial x}dxdy=\oint_{L}Qdy $$
对于上面两个式子,分别取$P=-y$,$Q=x$可得到:$$\begin{align}&\iint_{D}dxdy=A=-\oint_{L}ydx\\&\iint_{D}dxdy=A=\oint_{L}xdy\end{align}$$
其中,$A$为闭区域$D$的面积。根据式(1)和(2)也可得出:$$A=\frac{1}{2}\oint_{L}xdy-ydx$$
根据公式(2)来计算多边形面积,参考下面的示意图,曲线$L$由多段光滑的直线段$L_i$连接而成。由于$L$是分段光滑的,则有向曲线$L$上对坐标的曲线积分等于在光滑的各段上对坐标的曲线积分之和。即$A=\oint_Lxdy=\int_{L_0}xdy+...+\int_{L_6}xdy$
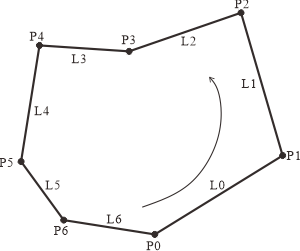
直线段$L_i$从点$(x_i,y_i)$到点$(x_{i+1},y_{i+1})$的参数方程为$L_i(t)=\left ((x_{i+1}-x_i)t+x_i,(y_{i+1}-y_i)t+y_i\right),\quad 0\leq t\leq 1$,于是对线段$L_i$的坐标积分为:$$\begin{aligned}\int_{Li}xdy&=\int_0^1((x_{i+1}-x_i)t+x_i)(y_{i+1}-y_i)dt\\&=(y_{i+1}-y_i)(x_it+\frac{1}{2}t^2(x_{i+1}-x_i))\big|_{0}^{1}\\&=\frac{1}{2}(x_{i+1}+x_i)(y_{i+1}-y_i)\end{aligned}$$
将每段结果相加得到多边形的面积为:$$\boxed{A=\sum_{i=0}^{n}\frac{(x_{i+1}+x_i)(y_{i+1}-y_i)}{2}}$$
其中,$n$为多边形顶点数-1,$(x_{n+1},y_{n+1})=(x_0,y_0)$。类似的,根据公式(1)可计算出多边形的面积为:$$\boxed{A=\sum_{i=0}^{n}\frac{(x_i-x_{i+1})(y_i+y_{i+1})}{2}}$$
多边形面积和顶点数组的顺-逆时针方向可以根据上面的公式计算,即如果是逆时针($L$为正向),则计算出的面积为正值;如果是顺时针,计算出的面积为负值。可参考下面的代码:
class Point: def __init__(self, x, y): self.x = x self.y = y def isCounterclockwise(points): s = 0 points_count = len(points) for i in range(points_count): point = points[i] point2 = points[(i + 1) % points_count] s += (point.x - point2.x) * (point.y + point2.y) return s > 0 def poly_area(points): s = 0 points_count = len(points) for i in range(points_count): point = points[i] point2 = points[(i + 1) % points_count] s += (point.x - point2.x) * (point.y + point2.y) return abs(s/2) if __name__ == "__main__": polygon1 = [Point(0,0), Point(0.5,0), Point(0.5,0.5), Point(0,1)] # counter-clockwise polygon2 = polygon1[::-1] # clockwise print(isCounterclockwise(polygon1), isCounterclockwise(polygon2)) # True, False print(poly_area(polygon1)) # 0.375
参考: