【模板】线性同余方程组

同余方程组

　　　所谓线性同余方程组，指的是将几个线性同余方程连理起来。形如下：

　　　　　　

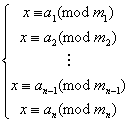
中国剩余定理

　　解同余方程组我们通常会使用中国剩余定理。这种算法最早是在《孙子算经》中所提到的：

有物不知其数，三三数之剩二，五五数之剩三，七七数之剩二。问物几何？

　　　　　　　　　　　　　　　　　　　　　　　　　　　　——【南北朝】《孙子算经》卷下第二十六题

三人同行七十稀，五树梅花廿一支，七子团圆正半月，除百零五使得知。

　　　　　　　　　　　　　　　　　　　　　　　　　　　　——《孙子歌诀》【明】程大位

　　具体的方案如下：

　　对上述定理的证明：

　　

　

扩展中国剩余定理

　　上面讲的办法相比于下面这个方法，实在是太优秀了（反正我很喜欢上面这种），可是它却有着十分令人不爽的限制条件，就是要求所有的m两辆互质。但是又有很多的毒瘤题他就不是互质比如说某不愿透露姓名的POJ2891，所以我们需要Get到一种方法，然我们能够摆脱那个限制。

　　那么，我们应该怎么办呢，我们先来考虑一下如果这个方程的个数为1个我们会怎么做，即问题可以转化为求解同余方程这么弱智的题当然是直接解得 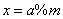呀，的确是如此，那如果我们在这个基础上再加入其他的方程呢？考虑n个有点麻烦，那我们从加入第二个开始考虑：

　

　　接着我们再把第三个方程加进去：

　

看了前三个之后想必各位都应该有了点感觉（没有的话可以自己尝试推一下第四个），我么直接来考虑一下加入第i + 1个方程的情况：

　　经过上面的归纳，我们发现我们可以通过n次扩欧将所需要的答案给求出来。代码如下：

#include<bits/stdc++.h>
using namespace std;
#define LL long long
const int MAX = 100005;

LL a[MAX], m[MAX], mod, mul, M;
int n;
inline LL read()
{
    LL x = 0; int w = 0; char ch = getchar();
    for(;!isdigit(ch); w |= (ch == '-') , ch = getchar());
    for(;isdigit(ch); x = (x << 3) + (x << 1) + (LL)(ch ^ 48), ch = getchar());
    return w ? -x : x;
}

inline LL Gcd(LL a, LL b)
    {
       return b == 0 ?  a : Gcd(b, a % b);
    }

LL exgcd(LL a, LL b, LL &x, LL &y)
    {
        if(b == 0)
            {
                x = 1, y = 0;
                return a;
            }
        LL gcd = exgcd(b, a % b, y, x);
        y -= x * (a / b);
        return gcd;
    }

LL smul(LL a, LL b, LL mod)
    {
        LL ret = 0;
        for(;b;)
            {
                if(b & 1)    ret = (ret + a) % mod;
                a = (a + a) % mod, b >>= 1;
            }
        return ret;
    }

bool Get_ans(LL a, LL b, LL c, LL & x, LL & y, LL &gcd)
    {
        gcd = exgcd(a, b, x, y);
        if(c % gcd)    return false;
        LL k = c / gcd, t = b / gcd;
        x = smul(x, k, t);
        x = ((x % t) + t) % t;
        return true;
    }

bool exChina(LL & ans)
    {
        LL y, x, gcd;
        M = m[1]; ans = a[1];
        for(int i = 2; i <= n; ++ i)
            {
                if(!Get_ans(M, m[i], (a[i] - ans % m[i] + m[i]) % m[i], x, y, gcd))    return false;
                ans = (ans + x * M);
                M = (M / gcd) * m[i];
                ans = (ans % M + M) % M;
            }
        ans = (ans % M + M) % M;
        return true;
    }

int main()
{    
    LL ans = 0;
    scanf("%d", &n);
    for(int i = 1; i <= n; ++ i)    m[i] = read(), a[i] = read();
    if(exChina(ans))    printf("%lld
", ans);
    else    printf("No solution
");
    return 0;
}