1、从Fibonacci函数的四种实现聊起。
Fibonacci数列,中文也译作斐波那契数列,相信大多数同学不会陌生,就是经典的兔子问题,以下图片内容来源于网络。
很清晰地,如上所述,如果把自然数到Fibonacci数列的映射看作一个函数U(n)的话,那么有U(n) = U(n-1) + U(n-2)。编码实现的话,自然是首选递归,Fibonacci数列的递归实现如下:
Fibonacci数列实现方法1-------递归
unsigned int Fibonacci_1(unsigned int n)
{
if ((n == 1) || (n == 2)) {
return 1;
}
return Fibonacci_1(n - 1) + Fibonacci_1(n - 2);
}看上去非常地简洁,非常地清晰,但是,有没有什么问题?有!而且是大问题,算法复杂度太高了,很容易发现算法复杂度为O(2^n)。展开来看,大概就是这么个情况。
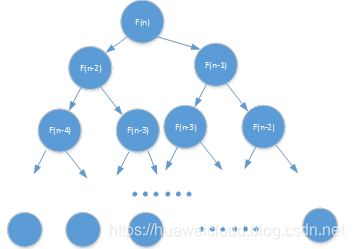
有没有办法可以优化一下呢?很容易发现,采用上述递归实现算法复杂度之所以高的原因就在于做了太多的重复计算。

到这里我们就要质疑一下,多问一句“有这个必要么?!”
当然没有!保存一下运算结果,以空间来换时间不可以么?来,试试看。
Fibonacci数列实现方法2-------递归+去重复计算
unsigned int Fibonacci_2(unsigned int n)
{
static unsigned int f[100] = {0};
if ((n == 1) || (n == 2)) {
return 1;
}
else if (0 != f[n]) {
return f[n];
}
f[n] = Fibonacci_2(n - 1) + Fibonacci_2(n - 2);
return f[n];
}看上去似乎要好一点了,但是性能如何呢?来来来,是骡子是马拉出来66,跑起来才知道。定义测试函数。
void testF(void)
{
long t1, t2;
unsigned int fn;
t1 = clock();
fn = Fibonacci_1(40);
t2 = clock();
if (t1 <= t2) {
printf("Fibonacci_1 run time =%u, result = %u
", t2 - t1, fn);
}
t1 = clock();
fn = Fibonacci_2(40);
t2 = clock();
if (t1 <= t2) {
printf("Fibonacci_2 run time =%u, result = %u
", t2 - t1, fn);
}
}实测结果

没有对比就没有伤害。
来,继续思考,是否还可以继续优化?实现方法2是以空间换时间,空间复杂度为O(n),时间复杂度,因对每个i<n,f(i)都只需要计算1次,因此时间复杂度也为O(n)。目测,时间复杂度基本上已无优化空间,那么空间复杂度呢?静态数组f是否必要?
![]()
回过头来再看递归关系:U(n) = U(n-1) + U(n-2),也就是说只要依次算出U(i),1<=i<n,就自然可以得到U(n),并且计算U(n)时,只需要知道U(n-1)和U(n-2)的值就可以。而对于U(i),i<n-2的值都用不到,保存这些东西干啥呢?由此出发,我们推演出代码实现方案3
Fibonacci数列实现方法3-------正向计算

看上去貌似好简单的样子,没有递归,没有对中间结果的保存,so easy!
再对比一下性能来看看:
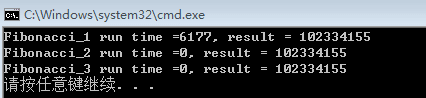
就是这么漂亮!
BTW:顺便提一句,事实上对于Fibonacci数列,是有通项公项可以直接计算的,这是高中奥数的基本功。
根据递推关系得特征根方程è X^2-X-1 = 0
解特征根方程得特征根è x1 = (1+5^(1/2))/2 x2 = (1-5^(1/2))/2
代入通项公式F(n) = C1*(x1)^n + C2*(x2)^n,F(1)=1,F(2)=1,解得
è C1=1/(5)^(1/2) C2= -1/(5)^(1/2),得通项公式
èF(n) = ![]()
,非本文重点介绍内容,故在此不作过多介绍,如有兴趣,可以私聊。
补充编码实现:
Fibonacci数列实现方法4------不动点通项公式
unsigned int Fibonacci_4(unsigned int n)
{
double sqrt5 = sqrt(5);
double root1 = (1 + sqrt5) / 2;
double root2 = (1 - sqrt5) / 2;
return (pow(root1, n) - pow(root2, n)) / sqrt5;
}注: 实现方法4,涉及开方,幂,以及除法等数学运算,受限于计算机精度限制,在n较大时,计算数值不准确,故不推荐。此外,仅为理论说明。
2、动态规划与递归的关系。
回过头来继续再看,Fibonacci数列实现方法2和Fibonacci数列实现方法3到底有什么差别,本质上来讲,没有差别。这是由Fibonacci数列的递推关系式决定的。实现方法3之所以空间复杂度低,那仅是由于Fibonacci的递推关系实在是太简单了,F(n)仅依赖于F(n-1)和F(n-2),如果递推关系再复杂一些,甚至依赖项的个数再与n相关,两者就更像了。
但是从实现设计的思想上来看,两者略有不同。
实现方案3是正向的来考虑,换种写法,就是标准的动态规划。

但是这种考虑方式略显得反人类。为什么这样说呢?作为技术面试官,我在面试时,喜欢出一些算法方面的问题,来考察应聘者对基本数据结构和算法的理解,对于Fibonacci数列,大多数应聘者,包括能力很强的程序员,都是按照递归来写的(问题是很少有考虑性能因素的,都采用的实现方案1),很少有人会用实现方案3,不太符合我们的思维模式。
实现方案2相对实现方案3要更符合我们的思维模式,递归嘛,只要注意到了递归的性能问题,就自然水道渠成了。如刚才提到的实现方案2本质上来讲也是动态规划,或者说跟动态规划没有差别,只要有递推关系存在,本质上就是一样的。动态规划相对于递归,仅仅是减少了些不必要的重复计算而已。递归当然也可以做得到。而且更附合我们的思维模式。
所以,总结一下,涉及递推送关系的算法问题,可以用动态规划思维解决的,用递归一样可以解决,关键在于要注意到算法性能,通过矩阵数组保存中间过程运算结果,从而避免不必要的重复计算。一句话,去除了重复计算的递归就是动态规划。
3、实战演练。
题目描述
给定一个正整数,我们可以定义出下面的公式:
N=a[1]+a[2]+a[3]+…+a[m];
a[i]>0,1<=m<=N;
对于一个正整数,求解满足上面公式的所有算式组合,如,对于整数 4 :
4 = 4;
4 = 3 + 1;
4 = 2 + 2;
4 = 2 + 1 + 1;
4 = 1 + 1 + 1 + 1;
所以上面的结果是 5 。
注意:对于 “4 = 3 + 1” 和 “4 = 1 + 3” ,这两处算式实际上是同一个组合!
解答要求时间限制:1000ms, 内存限制:64MB
输入
每个用例中,会有多行输入,每行输入一个正整数,表示要求解的正整数N(1 ≤ N ≤ 120) 。
输出
对输入中的每个整数求解答案,并输出一行(回车换行);
样例
输入样例 1 复制
4
10
20
输出样例 1
5
42
627
作者:张亮