演讲摘要(即论文摘要)

作者视频讲解:https://www.youtube.com/watch?v=WWWQXTb_69c&feature=youtu.be&t=20s
摘要
分布式训练的瓶颈为同步梯度和参数的高网络通信成本。在论文中,我们提出了三元梯度来加速分布式学习。只需要一个三元数组{-1,0,1}就可以减少通信时间。在梯度有界的前提下,我们数学证明了TerGrad的收敛性。在边界指导下,我们提出了分层的三元化和梯度裁剪来提高收敛性。实验证明可以提升准确性。
1.introdution
训练大规模模型的数据经常采用分布式系统。SGD通常作为优化算法,由于其高计算效率。
同步SGD:

缺点:延长通信时间
异步SGD:
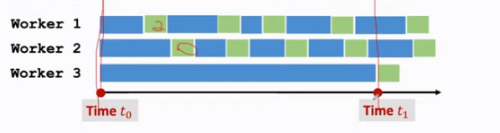
缺点:降低模型精度
目前加速分布式训练最常使用的是稀疏性和量化技术。
我们的工作属于梯度量化的范畴,这是一种正交的稀疏方法。TernGrad量化梯度为三元级{-1,0,1}来减少梯度并行的开销。更重要的是,我们提出了标量共享与参数定位,用一个低精度的梯度牵引来代替参数同步。
contribution:
- use ternary values for gradients to reduce communication
- prove the convergence of TernGrad in general by proposing a statistical bound on gradients
- propose layer-wise ternarizing and gradient clipping to move this bound closer toward the bound of standard SGD
- build a performance model to evaluate the speed of training methods with compressed gradients, like TernGrad
2.相关工作
2.1 Gradient sparsification(梯度稀疏化)
论文[27]提出了一种启发式梯度稀疏化方法。截断最小梯度,只传输剩余的大梯度。这种方法在不影响传输质量的前提下,减少了梯度通信。论文[31]也采用了类似的方法,但目标是稀疏恢复而不是加速训练。我们提出的方法与这些方法是正交的。
2.2 Gradient quantization(梯度量化)
论文[22]将权重、激活和梯度分别降到了1、2和6,当加速单一节点时损失了9.8%精确度
论文[30]用16位数字精度的硬件加速器在MNIST和CIFAR数据集上成功训练了神经网络
我们的工作是加速分布式训练通过降低通讯梯度到三元水平{-1,0,1}
论文[28]应用了1位SGD来加速分布式训练,实验证明了在语音应用中的有效性。
论文[32]提出来随机梯度旋转量化,将MNIST和CIFAR数据集的梯度精度降低到了4位。
论文[29]中的QSGD探索准确性和梯度精度之间的关系。梯度量化的有效性和QSGD的收敛可被证明。【论文29链接:https://arxiv.org/pdf/1610.02132.pdf】
TernGrad和论文[29]有相同的概念,但有以下三方面的改进:
- (1)我们从梯度统计界的角度证明了算法的收敛性。界限也揭示了为什么在QSGD中需要多个量化桶;
- (2)该界用于指导实践并启发分层三元化和梯度裁剪技术;
- (3)TernGrad使用三层梯度实现了0.92%的精度提高,在QSGD中的精度损失为1.73%。
3.Problem Formulation and Our Approach
3.1 Problem Formulation and TernGrad
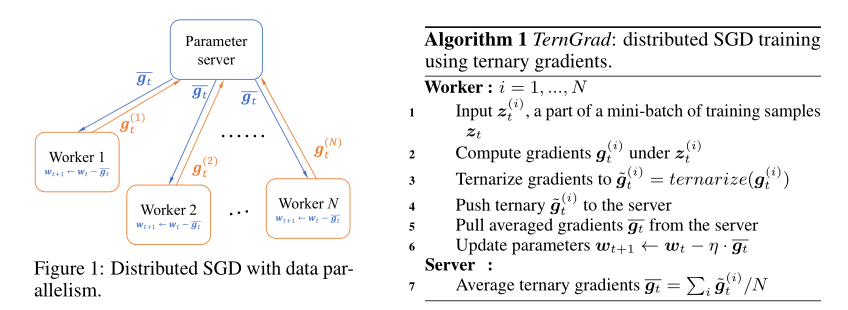
参数服务器在大多数应用中是用来保护分享的参数,在论文中我们用来保护分享的梯度。
TernGrad大多数步骤和传统的分布式训练相同,除了梯度在传给参数服务器之前会被量化为三元精度。更准确来讲,是为了减少梯度的通信量。
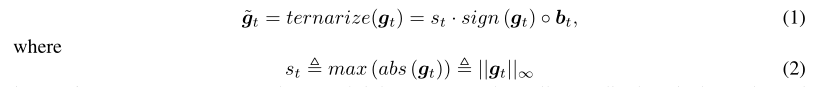
- s是标量,例如最大范式,可以对一个很小的振幅进行变化。
- ◦ 是Hadamard产品。
- sign(·)和abs(·)分别返回每个元素的标志和绝对值。

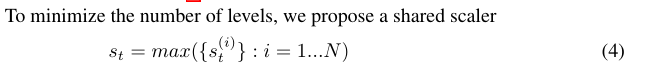
看不懂的话,看下图作者举的例子,一目了然:

3.2 Convergence Analysis and Gradient Bound(收敛性分析和梯度界线)
1.我们分析了在线学习系统框架中TernGrad的收敛性。在线学习系统将参数w调整为一系列观察值来最大化性能。每个观察值z是从未知分布中得知的,损失函数Q(z,w)用来测量参数w和输入z的系统性能。最小化目标就是损失预期。
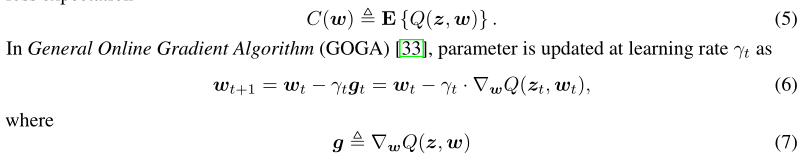
-
t表示迭代步骤中的每一步
-
E{g}是梯度是最小化的目标
在TernGrad 中,参数为:
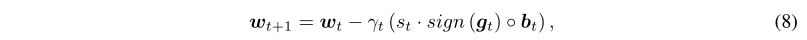
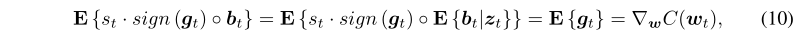
- 收敛性分析我们是采用论文[33]中GOGA的收敛性证明改编而成的,我们采用两个假设,用于分析GOGA的收敛性。(注:向量在这里表示为列向量)

剩下的没看懂。接下来就是实验证明部分了。
问题:
传输梯度的过程中梯度的信息是否会被泄露?是否可以通过梯度进行反推?
源码链接://download.csdn.net/download/weixin_45428522/12264387
PPT链接://download.csdn.net/download/weixin_45428522/12264378