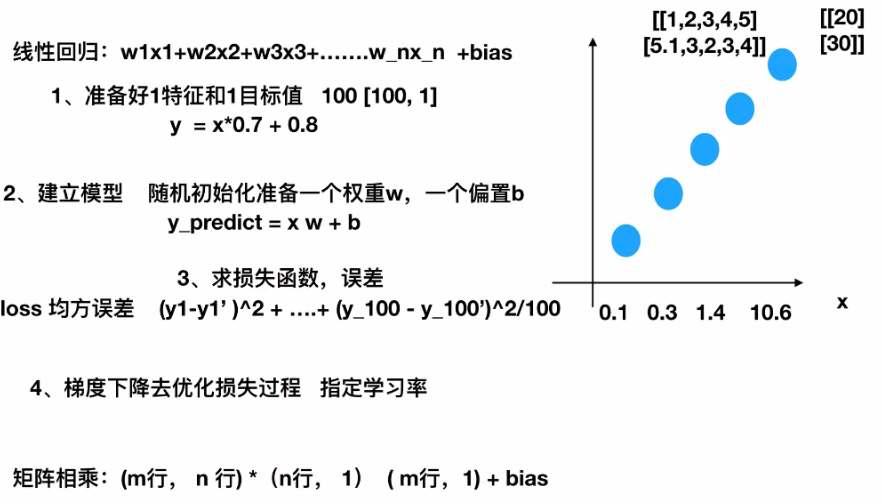
一、线性回归原理分析
二、实现线性回归所用到的api
1、Tensorflow运算API
矩阵相乘 tf.matmul(x, w)
平方 tf.square(error)
均值 tf.reduce_mean(error)
2、梯度下降API
tf.train.GradientDescentOptimizer(learning_rate) 梯度下降优化
learning_rate:学习率,一般为 method: return:梯度下降op
三、简单案例
import tensorflow as tf import os os.environ['TF_CPP_MIN_LOG_LEVEL']='2' # 1、训练参数问题:trainable # 学习率和步数的设置: # 2、添加权重参数,损失值等在tensorboard观察的情况 1、收集变量2、合并变量写入事件文件 # 定义命令行参数 # 1、首先定义有哪些参数需要在运行时候指定 # 2、程序当中获取定义命令行参数 # 第一个参数:名字,默认值,说明 tf.app.flags.DEFINE_integer("max_step", 100, "模型训练的步数") # 定义获取命令行参数名字 FLAGS = tf.app.flags.FLAGS def myregression(): """ 自实现一个线性回归预测 :return: None """ with tf.variable_scope("data"): # 1、准备数据,x 特征值 [100, 1] y 目标值[100] x = tf.random_normal([100, 1], mean=1.75, stddev=0.5, name="x_data") # 矩阵相乘必须是二维的 y_true = tf.matmul(x, [[0.7]]) + 0.8 with tf.variable_scope("model"): # 2、建立线性回归模型 1个特征,1个权重, 一个偏置 y = x w + b # 随机给一个权重和偏置的值,让他去计算损失,然后再当前状态下优化 # 用变量定义才能优化 # trainable参数:指定这个变量能跟着梯度下降一起优化 weight = tf.Variable(tf.random_normal([1, 1], mean=0.0, stddev=1.0), name="w") bias = tf.Variable(0.0, name="b") y_predict = tf.matmul(x, weight) + bias with tf.variable_scope("loss"): # 3、建立损失函数,均方误差 loss = tf.reduce_mean(tf.square(y_true - y_predict)) with tf.variable_scope("optimizer"): # 4、梯度下降优化损失 leaning_rate: 0 ~ 1, 2, 3,5, 7, 10 train_op = tf.train.GradientDescentOptimizer(0.1).minimize(loss) # 1、收集tensor tf.summary.scalar("losses", loss) tf.summary.histogram("weights", weight) # 定义合并tensor的op merged = tf.summary.merge_all() # 定义一个初始化变量的op init_op = tf.global_variables_initializer() # 定义一个保存模型的实例 saver = tf.train.Saver() # 通过会话运行程序 with tf.Session() as sess: # 初始化变量 sess.run(init_op) # 打印随机最先初始化的权重和偏置 print("随机初始化的参数权重为:%f, 偏置为:%f" % (weight.eval(), bias.eval())) # 循环训练 运行优化 for i in range(FLAGS.max_step): sess.run(train_op) print("第%d次优化的参数权重为:%f, 偏置为:%f" % (i, weight.eval(), bias.eval())) return None if __name__ == "__main__": myregression()
