BZOJ4238 : 电压
感谢这位dalao的文章:https://www.cnblogs.com/clrs97/p/4737869.html
这道题有利用dfs树的巧妙做法,但是仅仅是思路上的优化,这里我们总结下比较常规(?)的方法
首先分析题意,我们发现,环与一条边能否被选有着密切的关系
若图中有环,那么这条边必须在所有奇环的交,且不属于任何一个偶环
因为如果奇环中没有这条边的话就不能二分染色,而偶环有了就不能
因为环的特殊性,我们可以想到先做出个没有环的图,再逐个统计环的影响
所以我们先生成一个树/森林,再将非树边加入,统计经过每条边的奇环数和偶环数即可
但是也有可能在一个环上不只有一条非树边,对于这种由多个环组成的环怎么办呢?
答案是不用管他。。。
(以下图黑边为树边,红边为非树边)

1.奇环+奇环=偶环 新形成的偶环因为上面的边都没法经过所有奇环被自然淘汰了
2.偶环+偶环=偶环 反正都不能选了
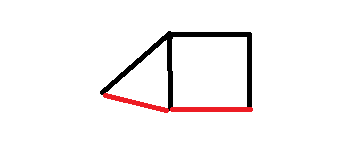
3.奇环+偶环=奇环 就是从奇环上扣去一部分,偶环的标记可以做到这一点
而具体的实现上使用了树链刨分加前缀和,我觉得dalao的代码非常妙,这里列一下
1.将边转化成了点,即u——v变成u—i—v,其中i是边的标号,这样非常方便打标记,边用的是1+n至m+n的编号
2.判断奇偶环使用的是两个端点深度的奇偶是否相同,这里为了方便维护了两个深度(dis,d)分别是真实深度和算上“边节点”的深度
还有一些关于自己要学习的码风
3.多用“,”,少用“;”
4.for的循环变量尽量全局
5.树刨代码简洁明了,值得学习(我太菜了555

1 #include<cstdio> 2 #define N 300010 3 using namespace std; 4 int n,m,i,x,y,dfn,f[N],e[N][2],need[N],h[N],v[N<<1],nxt[N<<1],et,d[N],size[N],son[N],top[N],loc[N],cnt,s[2][N],ans,dis[N],ban[N]; 5 inline int read(){ 6 int x=0;char ch=getchar();while(ch<'0'||ch>'9')ch=getchar(); 7 while(ch>='0'&&ch<='9'){x=x*10+ch-'0';ch=getchar();} 8 return x; 9 } 10 int F(int x){if(f[x]!=x)f[x]=F(f[x]);return f[x];} 11 inline void add(int x,int y){ 12 v[++et]=y;nxt[et]=h[x];h[x]=et; 13 v[++et]=x;nxt[et]=h[y];h[y]=et; 14 } 15 void dfs(int x,int y){ 16 size[x]=1,d[x]=d[f[x]=y]+1,dis[x]=dis[y]+(x<=n); 17 for(int k=h[x];k;k=nxt[k])if(v[k]!=y){ 18 dfs(v[k],x);size[x]+=size[v[k]]; 19 if(size[v[k]]>size[son[x]])son[x]=v[k]; 20 } 21 } 22 void dfs2(int x,int y){ 23 top[x]=y;loc[x]=++dfn; 24 if(son[x])dfs2(son[x],y); 25 for(int k=h[x];k;k=nxt[k])if(v[k]!=f[x]&&v[k]!=son[x])dfs2(v[k],v[k]); 26 } 27 inline void modify(int x,int y,int p){ 28 for(;top[x]!=top[y];x=f[top[x]]){ 29 if(d[top[x]]<d[top[y]]){int z=x;x=y;y=z;} 30 s[p][loc[top[x]]]++,s[p][loc[x]+1]--; 31 } 32 if(d[x]<d[y]){int z=x;x=y;y=z;} 33 s[p][loc[y]]++,s[p][loc[x]+1]--; 34 } 35 int main(){ 36 n=read();m=read(); 37 for(i=1;i<=n;i++)f[i]=i; 38 for(i=1;i<=m;i++){ 39 x=read(),y=read(),e[i][0]=x,e[i][1]=y; 40 if(F(x)!=F(y))f[f[x]]=f[y],add(x,i+n),add(y,i+n); 41 else need[i]=1; 42 } 43 for(i=1;i<=n;i++)if(!d[i])dfs(i,0),dfs2(i,i); 44 for(i=1;i<=m;i++)if(need[i]){ 45 x=e[i][0],y=e[i][1]; 46 if((dis[x]&1)^(dis[y]&1))ban[i]=1,modify(x,y,0);else modify(x,y,1),cnt++; 47 } 48 for(i=2;i<=dfn;i++)s[0][i]+=s[0][i-1],s[1][i]+=s[1][i-1]; 49 for(i=1;i<=m;i++)if(need[i]){ 50 if(!ban[i]&&cnt==1)ans++; 51 }else{ 52 if(!s[0][loc[i+n]]&&s[1][loc[i+n]]==cnt)ans++; 53 } 54 printf("%d",ans); 55 return 0; 56 }
