【bzoj3224】普通平衡树 && 平衡树大测速【平衡树】

题目链接

若专门来看平衡树测速，请略过这一部分，迅速往下！

GDKOI将近，蒟蒻的博主来复习平衡树怎么打了。
很伤心的是，开心地写了5种解法后，很多没有1A。看来比赛中对拍还是很重要的。只打了自己会的，非旋Treap什么的早就忘到九霄云外去了！
1 Treap

#include<cstdio>
#include<cstdlib>
const int N=100005;
int n,op,x,rt,cnt,val[N],rnd[N],siz[N],w[N],ch[N][2];
void maintain(int k){
    siz[k]=siz[ch[k][0]]+siz[ch[k][1]]+w[k];
}
void rotate(int &y,int md){
    int x=ch[y][md];
    ch[y][md]=ch[x][!md];
    ch[x][!md]=y;
    maintain(y);
    maintain(x);
    y=x;
}
void insert(int &k,int x){
    if(!k){
        k=++cnt;
        val[k]=x;
        rnd[k]=rand();
        siz[k]=w[k]=1;
        return;
    }
    siz[k]++;
    if(x==val[k]){
        w[k]++;
    }else if(x<val[k]){
        insert(ch[k][0],x);
        if(rnd[ch[k][0]]>rnd[k]){
            rotate(k,0);
        }
    }else{
        insert(ch[k][1],x);
        if(rnd[ch[k][1]]>rnd[k]){
            rotate(k,1);
        }
    }
}
void remove(int &k,int x){
    if(!k){
        return;
    }
    if(x==val[k]){
        if(w[k]>1){
            w[k]--;
            siz[k]--;
        }else if(ch[k][0]*ch[k][1]==0){
            k=ch[k][0]+ch[k][1];
        }else if(rnd[ch[k][0]]>rnd[ch[k][1]]){
            rotate(k,0);
            remove(k,x);
        }else{
            rotate(k,1);
            remove(k,x);
        }
    }else if(x<val[k]){
        siz[k]--;
        remove(ch[k][0],x);
    }else{
        siz[k]--;
        remove(ch[k][1],x);
    }
}
int rnk(int x){
    int k=rt,ret=1;
    while(k){
        if(x<=val[k]){
            k=ch[k][0];
        }else{
            ret+=siz[ch[k][0]]+w[k];
            k=ch[k][1];
        }
    }
    return ret;
}
int kth(int x){
    int k=rt;
    while(k){
        if(x>siz[ch[k][0]]&&x<=siz[ch[k][0]]+w[k]){
            return val[k];
        }else if(x<=siz[ch[k][0]]){
            k=ch[k][0];
        }else{
            x-=siz[ch[k][0]]+w[k];
            k=ch[k][1];
        }
    }
}
int main(){
    scanf("%d",&n);
    for(int i=1;i<=n;i++){
        scanf("%d%d",&op,&x);
        if(op==1){
            insert(rt,x);
        }else if(op==2){
            remove(rt,x);
        }else if(op==3){
            printf("%d
",rnk(x));
        }else if(op==4){
            printf("%d
",kth(x));
        }else if(op==5){
            printf("%d
",kth(rnk(x)-1));
        }else{
            printf("%d
",kth(rnk(x+1)));
        }
    }
    return 0;
}

2 Splay Tree

#include<cstdio>
const int N=100005;
int n,op,x,rt,cnt,tmp,val[N],ch[N][2],fa[N],siz[N],w[N];
int which(int k){
    return ch[fa[k]][1]==k;
}
void maintain(int k){
    siz[k]=siz[ch[k][0]]+siz[ch[k][1]]+w[k];
}
void rotate(int x){
    int y=fa[x],md=which(x);
    if(fa[y]){
        ch[fa[y]][which(y)]=x;
    }
    fa[x]=fa[y];
    ch[y][md]=ch[x][!md];
    fa[ch[y][md]]=y;
    ch[x][!md]=y;
    fa[y]=x;
    maintain(y);
    maintain(x);
}
void splay(int k,int f){
    while(fa[k]!=f){
        if(fa[fa[k]]!=f){
            rotate(which(k)==which(fa[k])?fa[k]:k);
        }
        rotate(k);
    }
    if(!f){
        rt=k;
    }
}
void insert(int pre,int &k,int x){
    if(!k){
        tmp=k=++cnt;
        val[k]=x;
        w[k]=siz[k]=1;
        fa[k]=pre;
        return;
    }
    siz[k]++;
    if(x==val[k]){
        w[k]++;
    }else if(x<val[k]){
        insert(k,ch[k][0],x);
    }else{
        insert(k,ch[k][1],x);
    }
}
void insert(int x){
    tmp=0;
    insert(0,rt,x);
    if(tmp){
        splay(tmp,0);
    }
}
void remove(int x){
    int k=rt;
    while(k){
        if(x==val[k]){
            break;
        }else if(x<val[k]){
            k=ch[k][0];
        }else{
            k=ch[k][1];
        }
    }
    splay(k,0);
    if(w[k]>1){
        w[k]--;
        siz[k]--;
    }else if(ch[rt][0]*ch[rt][1]==0){
        fa[ch[rt][0]+ch[rt][1]]=0;
        rt=ch[rt][0]+ch[rt][1];
    }else{
        k=ch[rt][0];
        while(ch[k][1]){
            k=ch[k][1];
        }
        splay(k,rt);
        ch[k][1]=ch[rt][1];
        fa[ch[rt][1]]=k;
        fa[k]=0;
        rt=k;
        maintain(rt);
    }
}
int rnk(int x){
    int k=rt,ret=1;
    while(k){
        if(x<=val[k]){
            k=ch[k][0];
        }else{
            ret+=siz[ch[k][0]]+w[k];
            k=ch[k][1];
        }
    }
    return ret;
}
int kth(int x){
    int k=rt;
    while(k){
        if(x>siz[ch[k][0]]&&x<=siz[ch[k][0]]+w[k]){
            return val[k];
        }else if(x<=siz[ch[k][0]]){
            k=ch[k][0];
        }else{
            x-=siz[ch[k][0]]+w[k];
            k=ch[k][1];
        }
    }
}
int main(){
    scanf("%d",&n);
    for(int i=1;i<=n;i++){
        scanf("%d%d",&op,&x);
        if(op==1){
            insert(x);
        }else if(op==2){
            remove(x);
        }else if(op==3){
            printf("%d
",rnk(x));
        }else if(op==4){
            printf("%d
",kth(x));
        }else if(op==5){
            printf("%d
",kth(rnk(x)-1));
        }else{
            printf("%d
",kth(rnk(x+1)));
        }
    }
    return 0;
}

3 替罪羊树

#include<cstdio>
#include<algorithm>
using namespace std;
const int N=100005;
const double alpha=0.75;
int n,op,x,rt,cnt,*goat,mmp[N],val[N],ch[N][2],del[N],siz[N],tot[N],pos[N];
int rnk(int x){
    int k=rt,ret=1;
    while(k){
        if(x<=val[k]){
            k=ch[k][0];
        }else{
            ret+=siz[ch[k][0]]+del[k];
            k=ch[k][1];
        }
    }
    return ret;
}
int kth(int x){
    int k=rt;
    while(k){
        if(del[k]&&x==siz[ch[k][0]]+1){
            return val[k];
        }else if(x<=siz[ch[k][0]]+del[k]){
            k=ch[k][0];
        }else{
            x-=siz[ch[k][0]]+del[k];
            k=ch[k][1];
        }
    }
}
void dfs(int k){
    if(!k){
        return;
    }
    dfs(ch[k][0]);
    if(del[k]){
        pos[++pos[0]]=k;
    }else{
        mmp[++mmp[0]]=k;
    }
    dfs(ch[k][1]);
}
void build(int &k,int l,int r){
    if(l>r){
        k=0;
        return;
    }
    int mid=(l+r)/2;
    k=pos[mid];
    build(ch[k][0],l,mid-1);
    build(ch[k][1],mid+1,r);
    siz[k]=siz[ch[k][0]]+siz[ch[k][1]]+1;
    tot[k]=tot[ch[k][0]]+tot[ch[k][1]]+1;
}
void rebuild(int &k){
    pos[0]=0;
    dfs(k);
    build(k,1,pos[0]);
}
void insert(int &k,int x){
    if(!k){
        if(mmp[0]){
            k=mmp[mmp[0]--];
        }else{
            k=++cnt;
        }
        val[k]=x;
        siz[k]=tot[k]=del[k]=1;
        ch[k][0]=ch[k][1]=0;
        return;
    }
    siz[k]++;
    tot[k]++;
    if(x<=val[k]){
        insert(ch[k][0],x);
    }else{
        insert(ch[k][1],x);
    }
    if(tot[k]*alpha<max(tot[ch[k][0]],tot[ch[k][1]])){
        goat=&k;
    }
}
void insert(int x){
    goat=NULL;
    insert(rt,x);
    if(goat){
        rebuild(*goat);
    }
}
void remove(int k,int x){
    if(!k){
        return;
    }
    siz[k]--;
    if(del[k]&&x==siz[ch[k][0]]+1){
        del[k]=0;
        return;
    }
    if(x<=siz[ch[k][0]]+del[k]){
        remove(ch[k][0],x);
    }else{
        remove(ch[k][1],x-siz[ch[k][0]]-del[k]);
    }
}
void remove(int x){
    remove(rt,rnk(x));
    if(siz[rt]<tot[rt]*alpha){
        rebuild(rt);
    }
}
int main(){
    scanf("%d",&n);
    for(int i=1;i<=n;i++){
        scanf("%d%d",&op,&x);
        if(op==1){
            insert(x);
        }else if(op==2){
            remove(x);
        }else if(op==3){
            printf("%d
",rnk(x));
        }else if(op==4){
            printf("%d
",kth(x));
        }else if(op==5){
            printf("%d
",kth(rnk(x)-1));
        }else{
            printf("%d
",kth(rnk(x+1)));
        }
    }
    return 0;
}

4 离散化+权值线段树

#include<cstdio>
#include<algorithm>
using namespace std; 
const int N=100005;
int n,cnt,rt,Hash[N],sum[N*20],ch[N*20][2];
struct query{
    int op,x;
}q[N];
void update(int &o,int l,int r,int k,int v){
    if(!o){
        o=++cnt;
    }
    sum[o]+=v;
    if(l==r){
        return;
    }
    int mid=(l+r)/2;
    if(k<=mid){
        update(ch[o][0],l,mid,k,v);
    }else{
        update(ch[o][1],mid+1,r,k,v);
    }
}
int rnk(int o,int l,int r,int k){
    if(l==r){
        return 1;
    }
    int mid=(l+r)/2;
    if(k<=mid){
        return rnk(ch[o][0],l,mid,k); 
    }else{
        return sum[ch[o][0]]+rnk(ch[o][1],mid+1,r,k);
    }
}
int kth(int o,int l,int r,int k){
    if(l==r){
        return l;
    }
    int mid=(l+r)/2;
    if(k<=sum[ch[o][0]]){
        return kth(ch[o][0],l,mid,k);
    }else{
        return kth(ch[o][1],mid+1,r,k-sum[ch[o][0]]);
    }
}
int main(){
    scanf("%d",&n);
    for(int i=1;i<=n;i++){
        scanf("%d%d",&q[i].op,&q[i].x);
        if(q[i].op!=4){
            Hash[++Hash[0]]=q[i].x;
        }
    }
    sort(Hash+1,Hash+Hash[0]+1);
    Hash[0]=unique(Hash+1,Hash+Hash[0]+1)-Hash-1;
    for(int i=1;i<=n;i++){
        if(q[i].op!=4){
            q[i].x=lower_bound(Hash+1,Hash+Hash[0]+1,q[i].x)-Hash;
        }
        if(q[i].op==1){
            update(rt,1,n,q[i].x,1);
        }else if(q[i].op==2){
            update(rt,1,n,q[i].x,-1);
        }else if(q[i].op==3){
            printf("%d
",rnk(rt,1,n,q[i].x));
        }else if(q[i].op==4){
            printf("%d
",Hash[kth(rt,1,n,q[i].x)]);
        }else if(q[i].op==5){
            printf("%d
",Hash[kth(rt,1,n,rnk(rt,1,n,q[i].x)-1)]); 
        }else{
            printf("%d
",Hash[kth(rt,1,n,rnk(rt,1,n,q[i].x+1))]);
        }
    }
    return 0;
}

5 乱入的普通二叉搜索树
其实我不会打，删除是乱打的，用了Treap的rotate。光速逃跑

#include<cstdio>
#include<cstdlib>
const int N=100005;
int n,op,x,rt,cnt,val[N],siz[N],w[N],ch[N][2];
void maintain(int k){
    siz[k]=siz[ch[k][0]]+siz[ch[k][1]]+w[k];
}
void rotate(int &y,int md){
    int x=ch[y][md];
    ch[y][md]=ch[x][!md];
    ch[x][!md]=y;
    maintain(y);
    maintain(x);
    y=x;
}
void insert(int &k,int x){
    if(!k){
        k=++cnt;
        val[k]=x;
        siz[k]=w[k]=1;
        return;
    }
    siz[k]++;
    if(x==val[k]){
        w[k]++;
    }else if(x<val[k]){
        insert(ch[k][0],x);
    }else{
        insert(ch[k][1],x);
    }
}
void remove(int &k,int x){
    if(!k){
        return;
    }
    if(x==val[k]){
        if(w[k]>1){
            w[k]--;
            siz[k]--;
        }else if(ch[k][0]*ch[k][1]==0){
            k=ch[k][0]+ch[k][1];
        }else{
            rotate(k,0);
            remove(k,x);
        }
    }else if(x<val[k]){
        siz[k]--;
        remove(ch[k][0],x);
    }else{
        siz[k]--;
        remove(ch[k][1],x);
    }
}
int rnk(int x){
    int k=rt,ret=1;
    while(k){
        if(x<=val[k]){
            k=ch[k][0];
        }else{
            ret+=siz[ch[k][0]]+w[k];
            k=ch[k][1];
        }
    }
    return ret;
}
int kth(int x){
    int k=rt;
    while(k){
        if(x>siz[ch[k][0]]&&x<=siz[ch[k][0]]+w[k]){
            return val[k];
        }else if(x<=siz[ch[k][0]]){
            k=ch[k][0];
        }else{
            x-=siz[ch[k][0]]+w[k];
            k=ch[k][1];
        }
    }
}
int main(){
    scanf("%d",&n);
    for(int i=1;i<=n;i++){
        scanf("%d%d",&op,&x);
        if(op==1){
            insert(rt,x);
        }else if(op==2){
            remove(rt,x);
        }else if(op==3){
            printf("%d
",rnk(x));
        }else if(op==4){
            printf("%d
",kth(x));
        }else if(op==5){
            printf("%d
",kth(rnk(x)-1));
        }else{
            printf("%d
",kth(rnk(x+1)));
        }
    }
    return 0;
}

于是我搞了一个平衡树测速，就用这道题，把n加到3000000（三百万），时限20s。这真是一(sang)棵(xin)赛(bing)艇(kuang)啊！
数据：1~3：随机，带删除。 4~6：随机，不带删除 。7：单调，带删除。8：单调，不带删除。9：半单调半随机，带删除。10：半单调半随机，不带删除。都是博主乱搞的，没有任何科学所在。
为了保证测试的准确性，所有的平衡树都是数组版的，寻址速度一样。
测试是在博主的win7电脑的lemon上进行的。
系统配置：

好，经过几十分钟漫长的调试和评测之后终于有结果了!
期间遇到最大的问题就是权值树的空间问题，因此n从5000000到4000000再降到3000000。
UPD：后来发现自己傻了。不用可持久化，空间只用开n*2。
好，上结果！

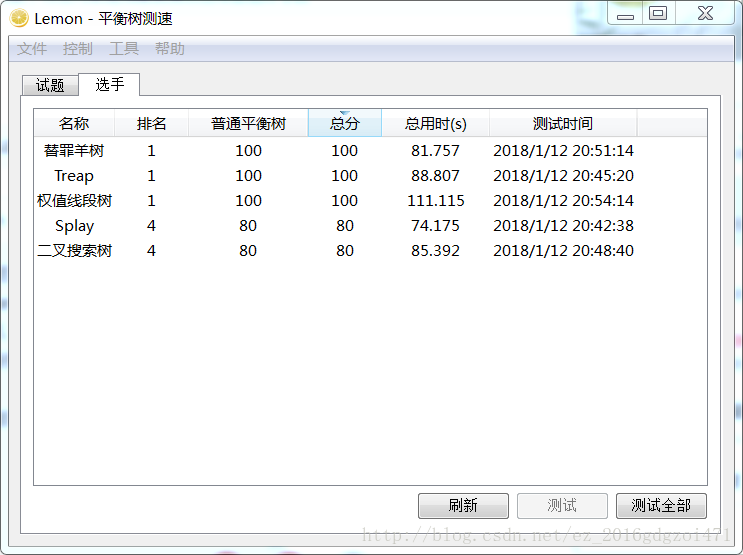
第一名：替罪羊树

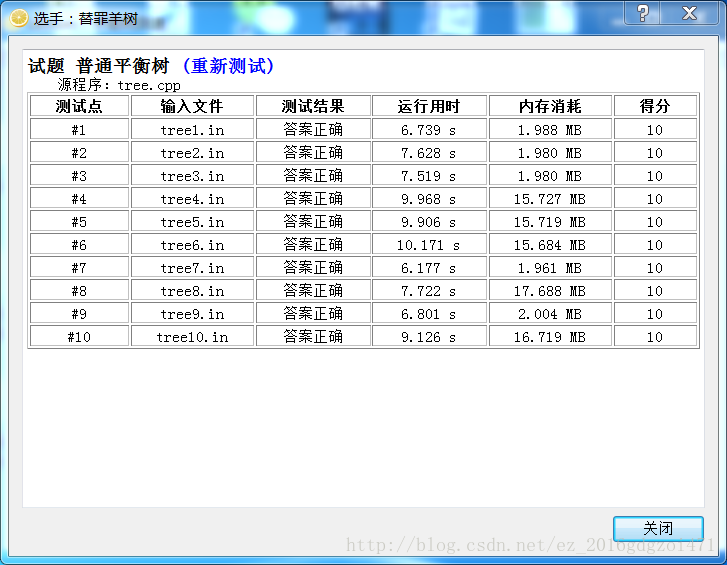
替罪羊树果然是跑得最快的。根据结果来看，它的效率只和树中的节点个数有关。再加上它又那么好写，是平衡树的很好的选择。如果裸的平衡树的话蒟蒻博主肯定会毅然选择它。
第二名：Treap

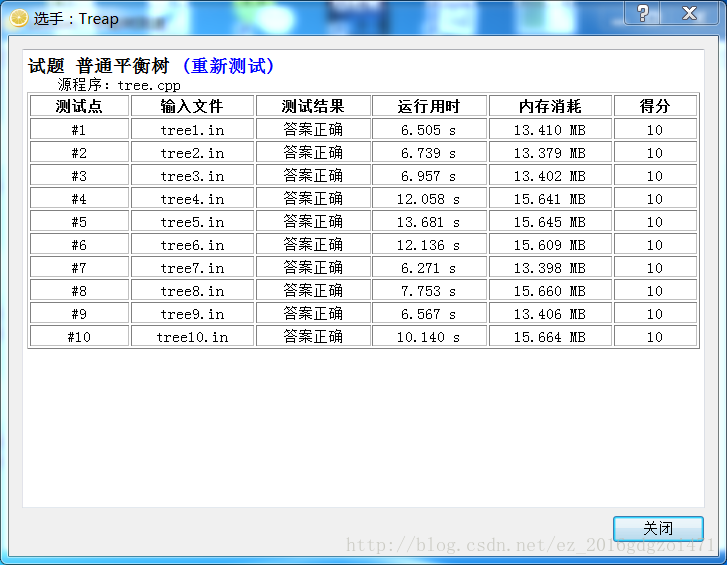
Treap也跑得很快，但效率可能会微微收到随机数的影响，相同规模的数据之间稍有起伏。编程复杂度也很低，总的来说也是很不错的。
第三名：离散化+权值线段树

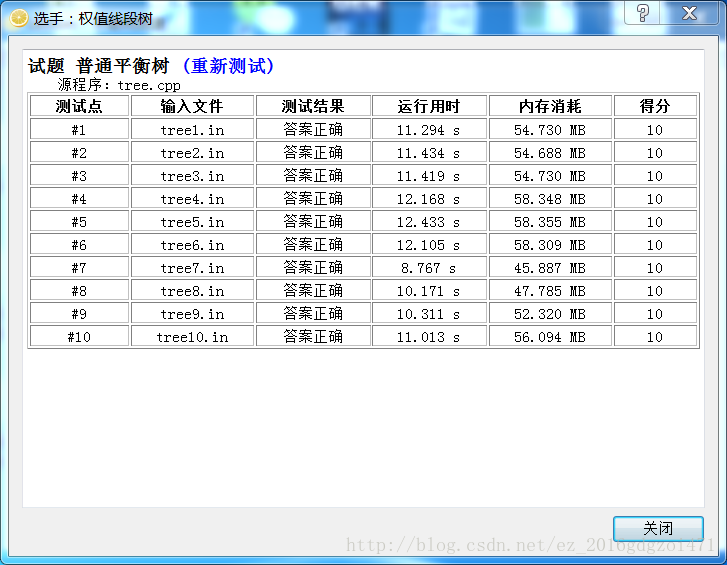
Ps：后来数组改小再测总用时只有96s，每个点各快了1s左右。
可以看出，权值线段树是效率最稳定的，因为它每次操作都是严格的logn，因此这种做法是不依靠数据的。如果除去离散化排序的复杂度，这种做法应该是最快的。但它的内存堪忧啊，nlogn，因此在内存允许的条件下，不卡时间的条件下，以及来不及写平衡树的时候可以用。
UPD：好吧我傻了，不可持久化就并没有内存问题。
第四名 Splay

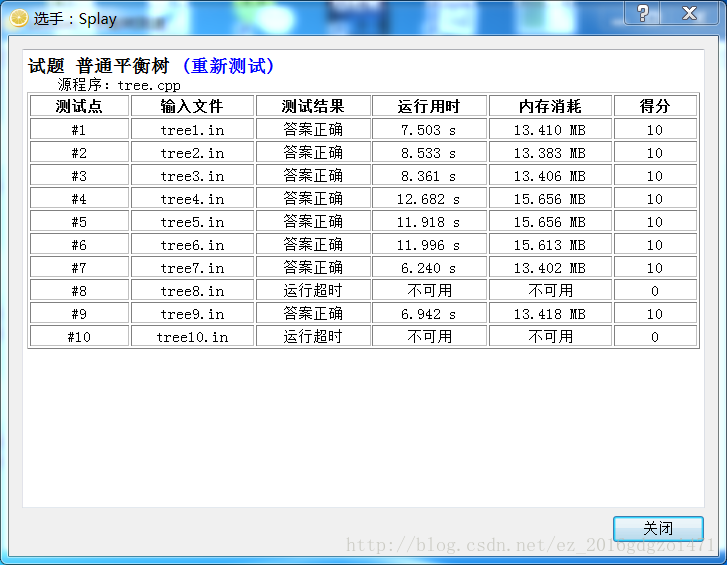
什么？Splay居然T了2个点！不知道是不是写矬了。随机数据下，splay都跑得过去，但一有单调数据且规模大（没有删除）起来，splay就慢了。而且众所周知splay常数巨大，因此splay很容易被卡。博主建议除了LCT和维护区间，都尽量不要用splay。
第五名 二叉搜索树

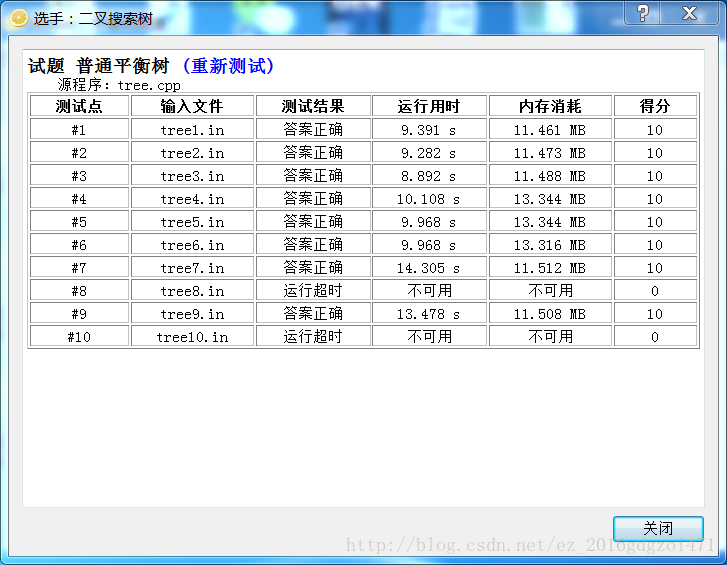
随机数据下跑得过去，但是单调数据随随便便可以卡它。因此坚决不要用！
总结一下，裸的平衡树替罪羊、Treap任选，如果要好写就用权值线段树，Splay只用来维护区间和LCT。
这次测试和观点仅供参考，若有高见请私信我!