一、杨辉三角形与组合数公式
1.使用组合数公式n!来实现
(1)利用组合数公式计算,通过对n的阶乘进行递归,实现求n!。
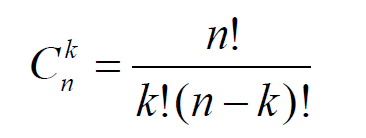
(2)程序流程图









(3)源程序代码
import java.util.Scanner;
public class Yhunsanjiao
{
public static void main(String[] args)
{
Scanner sc = new Scanner(System.in);
System.out.print("请输入一个数作为n:");
int n=sc.nextInt();
System.out.print("请输入一个数作为k:");
int k=sc.nextInt();
System.out.print("在n个元素中选取k个组合的所有结果数:"+zuheshu(k,n));
}
public static long zuheshu(int k,int n){
long i;
i=jiecheng(n)/(jiecheng(k)*jiecheng(n-k));
return i;
}
public static long jiecheng(int i){
long j=1;
if(i!=1)
j=i*jiecheng(i-1);
else
i=1;
return j;
}
}
(4)程序截图

2.使用递推方法用杨辉三角形计算组合数
(1)解题思想:
杨辉三角可以反映组合数的值,例如杨辉三角中第六排三列为10,即对应组合数c(5,2);通过递归建立杨辉三角,
再通过杨辉三角输出组合数值。
(2)程序流程图









(3)源程序代码
import java.util.Scanner;
public class YHSJ {
public static void main(String[] args)
{
// TODO Auto-generated method stub
Scanner sc = new Scanner(System.in);
System.out.print("请输入一个数作为n:");
int n=sc.nextInt();
System.out.print("请输入一个数作为k:");
int k=sc.nextInt();
System.out.print("在n个元素中选取k个组合的所有结果数:"+ditui(k,n));
}
public static int ditui(int n,int m)
{
int a[][]=new int[m+1][m+1];
for(int i=0;i<m+1;i++)
{
for(int j=i+1;j<m+1;j++)
{
a[i][j]=0;
}
for(int j=0;j<=i;j++)
{
if(j==0){ a[i][j]=1;}
else
{
a[i][j]=a[i-1][j-1]+a[i-1][j];
}
}
}
return a[m][n];
}
}
(4)截图

3.使用递归的方法用组合数递推公式计算
(1)解题思想:通过对组合数递推公式的递归实现,输出组合数的值
(2)程序流程图:
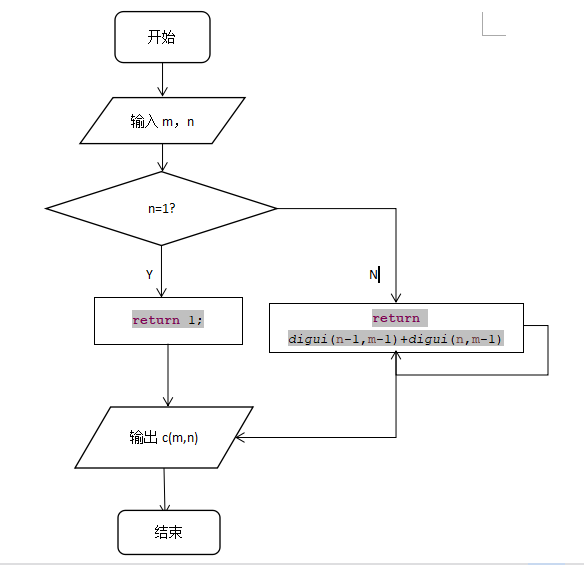
(3)源程序代码
import java.util.Scanner;
public class YH {
public static void main(String[] args)
{
// TODO Auto-generated method stub
Scanner sc = new Scanner(System.in);
System.out.print("请输入一个数作为n:");
int n=sc.nextInt();
System.out.print("请输入一个数作为k:");
int k=sc.nextInt();
System.out.print("在n个元素中选取k个组合的所有结果数:"+digui(k,n));
}
public static int digui(int n,int m)
{
if(n>m||n<0||m<0){return 0;}
if(n==1){return m;}
if(n==m){return 1;}
return digui(n-1,m-1)+digui(n,m-1);
}
}
(4)截图

二、递归编程解决汉诺塔问题,用Java实现
1.解决思想:
无论有多少个盘子,始终都有n个盘子从peg1移动到peg3,有n-1个盘子从peg3移动到peg2,也有n-1个盘子从peg1到peg2,
由此进行递归运算,解决问题。
2.程序流程图:
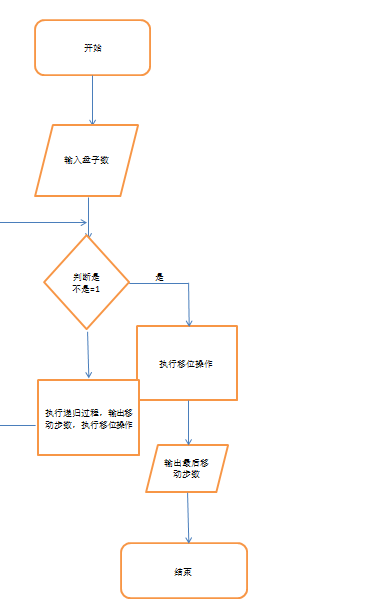
(3)源程序代码
import java.util.Scanner;
public class HANNUOTA
{
public static void moveDish(int level, char from, char inter, char to)
{
if (level == 1) {
System.out.println("从" + from + " 移动盘子" + level + " 号到" + to);
} else {
moveDish(level - 1, from, to, inter);
System.out.println("从" + from + " 移动盘子" + level + " 号到" + to);
moveDish(level - 1, inter, from, to);
}
}
public static void main(String[] args)
{
System.out.print("请输入盘子个数:");
Scanner sc = new Scanner(System.in);
int nDisks=sc.nextInt();
moveDish(nDisks, 'A', 'B', 'C');
}
}
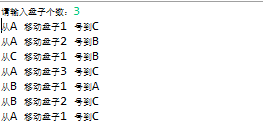
(4)实验截图
三、使用递归方式判断某个字串是否是回文
1.解题思路:先从键盘输入一个字符串,再利用String.charAT()函数得到字符串的各个位上的字符,进行比较,判断是否是回文字符串。
2.程序流程图:

(3)源程序代码:
import java.util.*;
public class HWZF
{
public static void main(String[] args)
{
Scanner s = new Scanner(System.in);
String str = null;
System.out.println("请输入您想输入的字符串:");
str = s.next();
System.out.println("您输入的是:");
System.out.println(str);
System.out.println("Is "+str+" a Palindrome?"+isPalindrome(str));
}
public static boolean isPalindrome(String s){
if(s.length()<=1){
return true;
}else if(s.charAt(0) != s.charAt(s.length()-1)){
return false;
}
return isPalindrome(s.substring(1,s.length()-1));
}
}
(4)结果截图:
