【实验项目名称】
基于贝叶斯分类器的手写数字识别
【实验目的】
在实验1模板匹配基础上,以贝叶斯分类器为判别函数,对模板化后的手写数字进行分类识别,达到熟练掌握贝叶斯分类器的目的。
【实验原理】
(1)利用样本计算每个数字的先验概率, 即每个数字出现的概率。
(2)读取标准化后的数字0~9,二值化,对每个数字进行等分区域分割,统计每个区域内的黑色像素点的个数,即为特征初值。利用公式计算类条件概率密度。
(3)利用贝叶斯求后验概率,最大的后验概率就是所属密度。
【实验要求】
给定数字0-9的原始样本集合,每个数字都有10个大小为240*240的样本图像。要求如下:
1、输出每种数字的先验概率
2、输出条件概率密度矩阵
3、输出测试结果
4、从统计意义上,给出每个数字的识别率。
5、对本实验进行总结
0.朴素贝叶斯;
1.流程图:
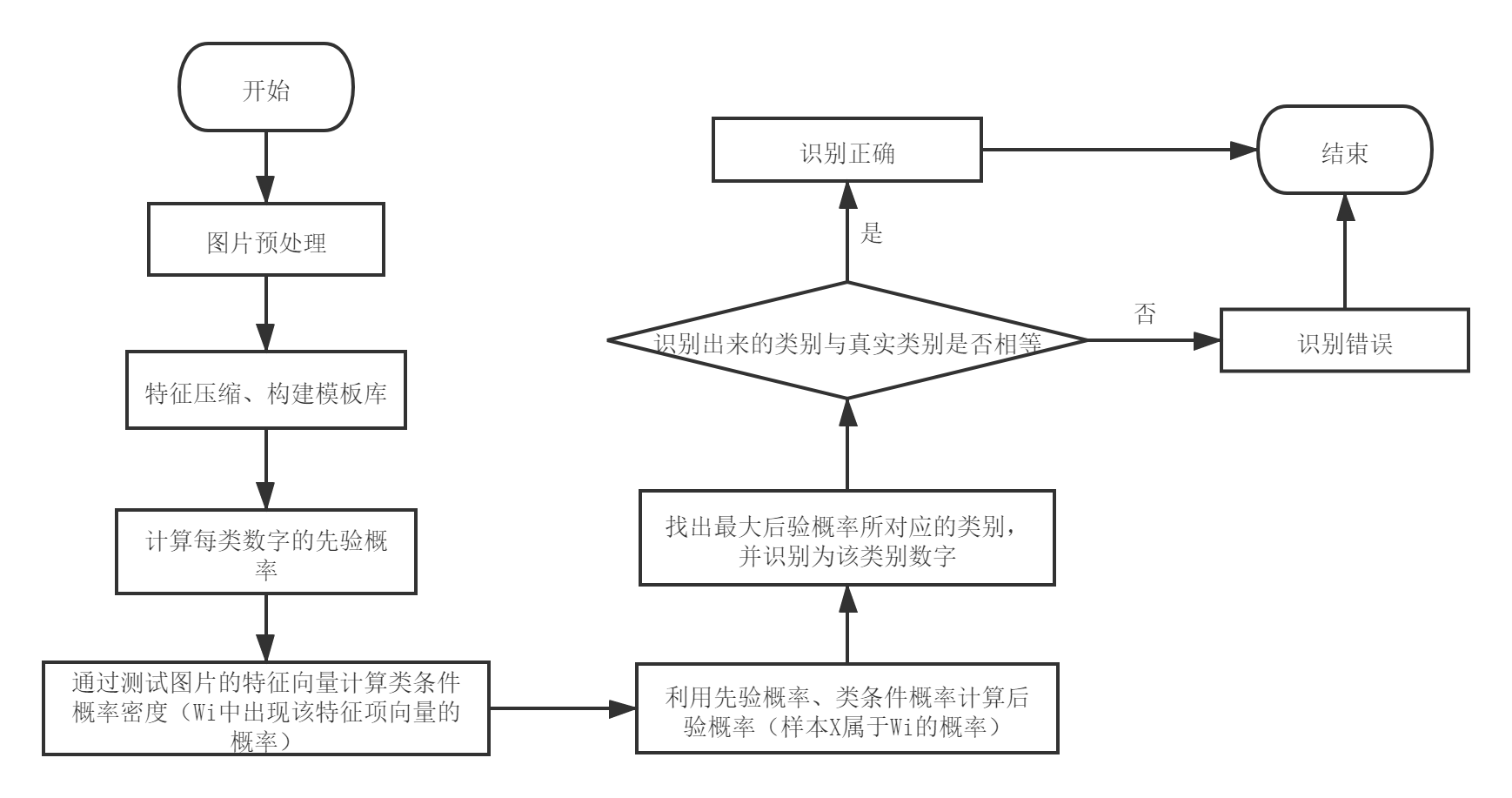
2.三种概率的计算与分析:
先验概率: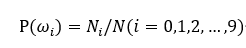 其中N为总样本数,Ni为每类样本的个数,由此可以计算出每类样本的先验概率。
其中N为总样本数,Ni为每类样本的个数,由此可以计算出每类样本的先验概率。
类条件概率: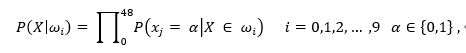
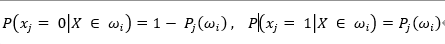
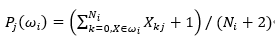 --公式4
--公式4
类条件概率:在特征空间ωi中出现样本特征X的概率,即为每个数字的特征空间中出现X的概率,所以针对每一个测试样本,需要计算出十个类条件概率。每个类条件概率通过 X 的每个特征在该类特征库里所占的比例来确定(公式4),最后通过各特征独立,直接相乘计算出来。
后验概率: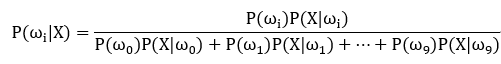
后验概率:样本特征X属于ωi的概率。利用先验概率、类条件概率,计算得到后验概率(一个test样本对应十个后验概率),其中概率最大的类别即为识别出来的类别。
3.测试结果(部分截图):
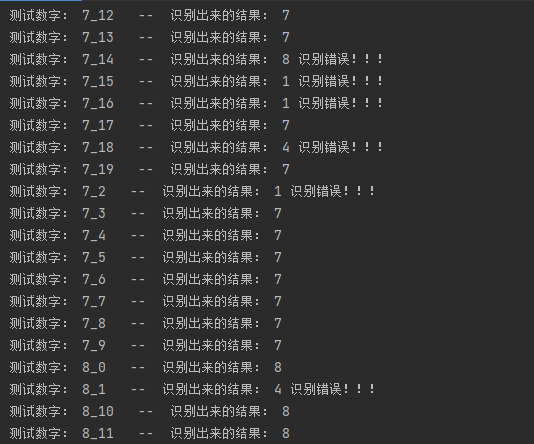
4.统计意义上的识别率:
数字 0 识别的正确率 = 85.00% ,错误率 = 15.00%
数字 1 识别的正确率 = 85.00% ,错误率 = 15.00%
数字 2 识别的正确率 = 65.00% ,错误率 = 35.00%
数字 3 识别的正确率 = 50.00% ,错误率 = 50.00%
数字 4 识别的正确率 = 65.00% ,错误率 = 35.00%
数字 5 识别的正确率 = 40.00% ,错误率 = 60.00%
数字 6 识别的正确率 = 60.00% ,错误率 = 40.00%
数字 7 识别的正确率 = 70.00% ,错误率 = 30.00%
数字 8 识别的正确率 = 60.00% ,错误率 = 40.00%
数字 9 识别的正确率 = 45.00% ,错误率 = 55.00%
5.关于错误率较大的分析:
一是由于图片结构的原因,白色字符区域过小,背景区域过大,并且特征压缩(降维)比较严重,可以适当保留更多的特征,当然保留更多特征带来的是更为庞大的计算量;二是朴素贝叶斯假定特征之间相互独立,当数据之间独立性较大时,分类效果较好,反之,当各属性之间存在关联时,会导致分类效果大大降低。显然,其特征之间存在关联。
6.代码:

1 # Bayes手写数字识别 2 import os 3 import Function 4 # 1.样本特征,不需预处理 5 # 2.图像压缩表示,28*28——7*7,存储于(picture_bayes(i).txt) 6 # 3.根据数字类别分别存储于不同的txt 7 root_dir = "E:/train-images" # 训练数据集 8 file_bayes = [] 9 for i in range(10): 10 file_bayes.append(open("E:/PatternRecognition/pic_txt/picture_bayes" + str(i) + ".txt", 'w')) # 覆盖写模式 11 sum_num = 0 12 Priori_pro = [0, 0, 0, 0, 0, 0, 0, 0, 0, 0] 13 for fl in os.listdir(root_dir): # 循环处理所有train图片 14 img_str = fl[0:-4] + ":" + Function.Image_Compression(root_dir + '/' + fl) # 图像压缩,返回压缩数据流 15 file_bayes[eval(fl[0])].write(img_str + ' ') # 压缩后的图像数据写入文本存储 16 Priori_pro[eval(fl[0])] += 1 # 统计每一类数字的个数 17 sum_num += 1 18 for i in range(10): 19 file_bayes[i].close() 20 # 3.bayes概率计算,先验概率、类条件概率、后验概率 21 # 先验概率--Priori_pro 22 for i in range(10): 23 Priori_pro[i] = Priori_pro[i] / sum_num 24 # 类条件概率--Class_pro && 后验概率--Posterior_pro 25 Class_pro = [0, 0, 0, 0, 0, 0, 0, 0, 0, 0] # 某个样本的类条件概率 26 Posterior_pro = [0, 0, 0, 0, 0, 0, 0, 0, 0, 0] # 某个样本的后验概率 27 Correct_rate = [0, 0, 0, 0, 0, 0, 0, 0, 0, 0] # 识别率 28 ############ 29 root_dir = "E:/test-images" # 测试test-images数据集 30 for fl in os.listdir(root_dir): # 循环处理所有test图片 31 class_pic = 0 # 比较得出后验概率最大的图片类别 32 max_pxh = 0 # 最大的后验概率 33 px_h_deno = 0 # 后验概率中的分母 34 test_img_str = Function.Image_Compression(root_dir + '/' + fl) 35 for i in range(10): # 计算类条件概率 36 Class_pro[i] = Function.Class_conditional_pro(test_img_str, i) 37 px_h_deno += Priori_pro[i] * Class_pro[i] 38 # print("{:.3e}".format(Class_pro[i]), end=" ") 39 for i in range(10): # 计算后验概率 40 Posterior_pro[i] = Priori_pro[i] * Class_pro[i] / px_h_deno 41 if max_pxh < Posterior_pro[i]: # 根据后验概率判断分类 42 max_pxh = Posterior_pro[i] 43 class_pic = i 44 if class_pic == eval(fl[0]): 45 print("测试数字:", fl[0:-4], " -- 识别出来的结果:", class_pic) # 数字的识别结果 46 Correct_rate[class_pic] += 1 47 else: 48 print("测试数字:", fl[0:-4], " -- 识别出来的结果:", class_pic, "识别错误!!!") 49 # print() 50 print("------------------------------------------------") 51 for i in range(10): 52 print("数字 {:d} 识别的正确率 = {:.2f}% ,错误率 = {:.2f}%".format(i, Correct_rate[i]*5, 100 - Correct_rate[i]*5)) 53 print("success!")
Class_conditional_pro(test_str, n)
(应该设计为,一次读取一行数据,然后同时处理49位数字,而非读取49次文件,不过都可实现)

1 ####################### 2 # 计算Pj(Wi),在此基础上计算P(X/Wi) 3 # 返回一个double类型数据,为在某一类数字(0-9)的特征空间中出现X的概率 4 # 某类数字的特征空间中出现该样本X的概率 5 ####################### 6 def Class_conditional_pro(test_str, n): 7 file = open("E:/PatternRecognition/pic_txt/picture_bayes" + str(n) + ".txt", 'r') # 只读模式 8 p_x_wi = 1.0 9 for i in range(len(test_str)): 10 sum_pj_wi = 0 11 while True: 12 line = file.readline() 13 if not line: # 已读完整个文档,光标返回开头,结束此次匹配 14 file.seek(0) 15 break 16 train_str = line[-50:-1] 17 sum_pj_wi += eval(train_str[i]) 18 if eval(test_str[i]) == 1: 19 p_x_wi *= (sum_pj_wi + 1) / (100 + 2) 20 else: 21 p_x_wi *= 1 - (sum_pj_wi + 1) / (100 + 2) 22 file.close() 23 return p_x_wi
2021-04-30
