题目大意:
给定一个数 x,设它十进制展从高位到低位上的数位依次是 a0, a1, ..., an - 1,定义交错和函数:
f(x) = a0 - a1 + a2 - ... + ( - 1)n - 1an - 1
例如:
f(3214567) = 3 - 2 + 1 - 4 + 5 - 6 + 7 = 4
给定
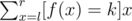
输入
输入数据仅一行包含三个整数,l, r, k(0 ≤ l ≤ r ≤ 1018, |k| ≤ 100)。
输出
输出一行一个整数表示结果,考虑到答案可能很大,输出结果模 109 + 7。
提示
对于样例 ,满足条件的数有 110 和 121,所以结果是 231 = 110 + 121。
更多样例:
| Input |
| 4344 3214567 3 |
| Output |
| 611668829 |
| Input |
| 404491953 1587197241 1 |
| Output |
| 323937411 |
| Input |
| 60296763086567224 193422344885593844 10 |
| Output |
| 608746132 |
| Input |
| 100 121 -1 |
| Output |
| 120 |
样例输入
100 121 0
样例输出
231
题目分析:定义状态dp(len,x,k)表示长度为len,开头数字为x,交错和为k的所有数之和,num(len,x,k)为上述状态的数的个数。则通过递推即可得到这两个状态组,然后构造答案即可。
ps:这道题贼恶心。。。每一步加或乘运算后必须取余,否则结果一定错误。
代码如下:
# include<iostream>
# include<cstdio>
# include<map>
# include<set>
# include<queue>
# include<vector>
# include<list>
# include<cstring>
# include<algorithm>
using namespace std;
# define LL long long
const int N=1000000000;
const int mod=1000000007;
int bit[20];
LL num[25][10][205];
LL dp[25][10][205];
LL base[20];
bool ok(int x)
{
return x>=-100&&x<=100;
}
void init()
{
base[0]=base[1]=1;
for(int i=2;i<=20;++i)
base[i]=(base[i-1]*10)%mod;
memset(num,0,sizeof(num));
memset(dp,0,sizeof(dp));
for(int i=0;i<10;++i){
num[1][i][i+100]=1;
dp[1][i][i+100]=i;
}
int flag=1;
for(int i=1;i<20;++i){
flag*=-1;
for(int j=0;j<10;++j){
for(int k=-100;k<=100;++k){
for(int l=0;l<10;++l) if(ok(k+flag*l)){
num[i+1][j][k+flag*l+100]+=num[i][j][k+100];
num[i+1][j][k+flag*l+100]%=mod;
dp[i+1][j][k+flag*l+100]+=((dp[i][j][k+100]*10)%mod+(num[i][j][k+100]*l)%mod)%mod;
dp[i+1][j][k+flag*l+100]%=mod;
}
}
}
}
}
LL solve(LL x,int k)
{
if(x<0) return 0ll;
LL temp=x;
bit[0]=0;
while(x>0){
bit[++bit[0]]=x%10;
x/=10;
}
LL res=0;
for(int i=1;i<bit[0];++i)
for(int j=1;j<10;++j){
res+=dp[i][j][k+100];
res%=mod;
}
int t=0;
int flag=1;
LL tt=0ll;
for(int i=bit[0];i>=1;--i){
int low=(i==bit[0])?1:0;
for(int j=low;j<bit[i];++j){
LL tres=((tt*num[i][j][(k-t)/flag+100])%mod+dp[i][j][(k-t)/flag+100])%mod;
res=(res+tres)%mod;
}
t+=flag*bit[i];
tt=(tt+(bit[i]*base[i])%mod)%mod;
flag*=-1;
}
if(t==k)
res=(res+temp)%mod;
return res;
}
int main()
{
init();
LL k,l,r;
//freopen("in.txt","r",stdin);
while(~scanf("%lld%lld%d",&l,&r,&k))
{
LL a=solve(r,k);
LL b=solve(l-1,k);
if(a<b) a+=mod;
printf("%lld
",a-b);
}
return 0;
}