信息安全系统设计基础第四周学习总结
位:孤立地讲,单个的位不是非常有用。然而,当把位组合在一起,再加上某种解释,即给不同的可能为模式赋予含义,我们就能够表示任何有限集合的元素。
三种最重要的数字表示:
无符号,补码,浮点数。
逆向角度思考安全漏洞的产生:
当你正向编写代码的时候,你是按照自己想使用代码的方式来理解代码;但是由于可能存在的编写不严谨的情况,这句完成的代码可能本身还有另外的理解方式。从逆向角度看,假如你从已经写好的代码反推其含义时,发现可能读出的含义与代码的初衷不同,就会导致BUG或者漏洞。
2.1信息存储
C语言的一个指针的值,都是某个存储块的第一个字节的虚拟地址。
2.1.1 十六进制表示法
当值X是2的非负整数n次幂时,X的二进制就是1后面跟n个0。当n表示成i+4j的形式,其中0<=i<=3,我们可以把X写成开头的十六进制数字为1(i=0),2(i=1),4(i=2),8(i=3),后面跟着j个十六进制的0。
例如,X=2048=2的11次方,我们有n=11=3+4*2,从而得到十六进制表示0x800。
PS:进制转换,可以用二进制做中间结果。
gcc -m32可以在64位环境产生32位代码。
2.1.4 寻址和字节顺序
小端法:最低有效字节在最前面,“高对高,低对低”,是大多数intel兼容机,包括IBM和Sun的个人intel兼容处理器的计算机使用的规则。
例如:变量x为int,位于地址0x100,十六进制值为0x01234567。
小端法:
地址: 0x100 0x101 0x102 0x103
67 45 23 01
在0x01234567中,高位字节为0x01,低位字节为0x67。
PS:字节顺序是网络编程的基础。
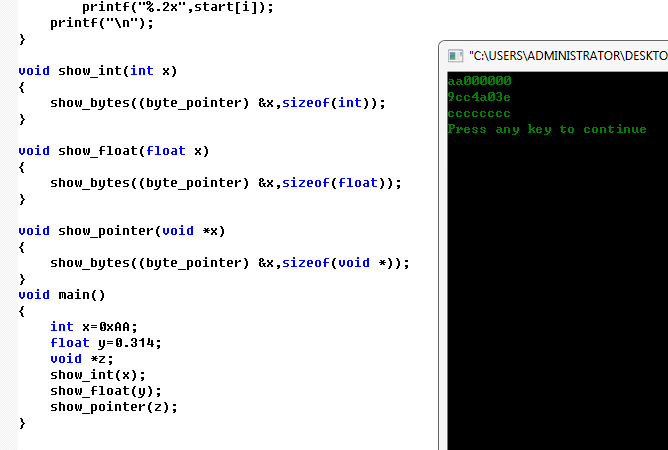
PS:P28教材代码运行
2.1.7 布尔代数简介
逻辑运算:~ & 0 1 | 0 1 ^ 0 1(异或)
0 1 0 0 0 0 0 1 0 0 1
1 0 1 0 1 1 1 1 1 1 0
位运算:结果是位向量
0110 0110 0110
&1100 |1100 ^1100 ~1100
0100 1110 1010 0011
PS:与或非均可用“与非”或者“或非”来表达,因此,只要一个与非门,就可以完成所有的逻辑运算。
掩码:通过指定一个位向量掩码,有选择地使能或者不能屏蔽一些信号,其中某一位位置上为1时,表明信号i是有效的,而0表明该信号是被屏蔽的。因而,这个掩码表示的就是设置为有效信号的集合。
2.2整数表示
两种方式:1.非负数 2.负数,零和正数
2.2.1 整型数据类型
整型:表示有限范围的整数
PS:long long 在ISO C99 中引入,需要至少8个字节表示。
最小值-9 223 372 036 854 775 808
最大值 9 223 372 036 854 775 807
编译时要使用 gcc -std=C99
2.2.3 补码编码
B2Tw表示长度为w的补码编码,其中,将字的最高有效位解释为负权。
例如:B2T4([0001])=-0*2^3+0*2^2+0*2^1+1*2^0= 1
B2T4([0101])=-0*2^3+1*2^2+0*2^1+1*2^0= 5
B2T4([1011])=-1*2^3+0*2^2+1*2^1+1*2^0=-5
B2T4([1111])=-1*2^3+1*2^2+1*2^1+1*2^0=-1
2.2.4 有符号数和无符号数之间的转换
对大多数C语言实现而言,处理同样字长的有符号数和无符号数之间相互转换的一般规则是:
数值可能会改变,但是位模式不变。
一个有符号数x和与之对应的无符号数T2Uw(x)之间的关系:
T2Uw(x)= x+2^w , x<0
x , x>=0
2.2.5 C语言中的有符号数和无符号数
当C语言执行一个运算,若一个运算数有符号而另一个运算数无符号,C语言会隐式地将有符号强转为无符号,并假设两者都非负,执行运算。
PS:要想让负数等于正数,可以让这个负数和这个正数的无符号形式相等,再在对比时将两者之一强转为无符号形式,即可。
2.2.6 扩展一个数字的位表示
0扩展:将一个无符号数转换为一个更大的数据类型,在表示的开头添加0。
符号扩展:将一个补码数字转换为一个更大的数据类型,在表示中添加最高有效位的值的副本。
2.2.8 关于有符号数和无符号数的建议
float sum_elements(float a[], unsigned length)
{
int i;
float result = 0;
for(i = 0; i< = length-1; i++)
result += a[i];
return result;
}
在2.25的代码中,无符号数0减去1,会导致-1被强转为对应无符号数,从而得到UMax,又因为i始终小于UMax,这会使程序进入超越数组长度的循环,出现错误。
2.3 整数运算
2.3.1 无符号加法
现定义参数x和y的运算+uw,这里0<=x,y<2^w:
x +uw y = x + y ,x+y<2^w;
x + y - 2^w , 2^w <= x+y <2^w+1;
一个算术运算溢出,是指完整的整数结果不能放到数据类型的字长限制中去。
让整数运算溢出:让无符号加法的和大于等于2^w。
避免溢出: 让无符号加法的的和小于2^w。
2.3.2 补码加法
范围在-2^w-1<=x,y<=(2^w-1)-1之内的x和y实施运算+tw :
x +tw y = x + y - 2^w , 2^w-1 <= x+y 正溢出
x + y ,-2^w-1 <= x+y < 2^w-1 正常
x + y + 2^w , x+y < -2^w-1 负溢出
2.3.3 补码非
-2^w-1 <= x < 2^w-1
-tw x = -2^w-1 ,x= -2^w-1
-x ,x> -2^w-1
2.3.4 无符号乘法
x *uw y =(x*y)%2^w
2.3.5 补码乘法
x *tw y =U2Tw((x*y)%2^w)
2.3.8 关于整数运算的最后思考
1.“整数”运算实际上是一种模运算形式。
2.表示数字的有限字长限制了可能的值得取值范围,结果运算可能溢出。
3.补码使用了与执行无符号算术相同的位级实现。
4.在书写整数常数和调用函数库时,特别要注意unsigned数据类型。
2.4 浮点数
IEEE标准754详细制定了表示浮点数及其运算的标准,后来被称为IEEE浮点。
2.4.1 二进制小数
0.111…1表示刚好小于1的数,可以用简单表示法1.0-ε来表示。
不精确性:小数的二进制表示法只能表示那些能被写成x*2^y的数,其他的值只能近似表示。
舍入:当一个数不能被准确地表示为一种格式时,就必须向上调整或者向下调整,就会出现舍入。
2.4.2 IEEE的浮点表示
IEEE浮点标准:V=(-1)^s * M * 2^E
符号:s确定正(s=0)还是负(s=1)
尾数:M是一个二进制小数,它的范围是1~2-ε,或者是0~1-ε。
n位小数字段frac=fn-1…f1f0编码尾数M
阶码:E的作用是对浮点数加权,这个权重是2的E次幂(可能是负数)。
k位阶码字段exp=ek-1…e1e0编码阶码E
float:s一位,k=8,n=23,得到一个32位的表示
double:s一位,k=11,n=52,得到一个64位的表示
1.规格化的值:
exp的位模式既不全为0(数值0),也不全为1(单精度数值255,双精度数值2047)
2.非规格化的值:
阶码域全为0
3.特殊值:
阶码全为1
整数与浮点数表示同一个数的关系:
整数12345(0x3039)表示成二进制为11000000111001,共有14位,将二进制小数点左移13位,
即:1.1000000111001(2)*2^13。
IEEE单精度编码:
小数字段:(去开头1,末尾加上23-(14-1)=10个0)[10000001110010000000000]
阶码字段:13+偏置量127=140,[10001100]
符号位:0
[01000110010000001110010000000000]
单精度浮点值12345.0:0x4640E400与整数12345(0x3039)重复部分:13位:1000000111001。
2.4.4 舍入
方式 1.40 1.60 1.50 2.50 -1.50
向偶数 1 2 2 2 -2
向0 1 1 1 2 -1
向下 1 1 1 2 -2
向上 2 2 2 3 -1
二进制舍入法可以应用于二进制小数。将最低有效位的值0认为是偶数,值1认为是奇数。
对形如XX…X.YY…Y100…的位模式表示在两个可能的结果正中间的值,并且我们倾向于使最低有效位为0。
2.4.6 C语言中的浮点数
若int为32位:
从int到float,数字不会溢出,可能舍入
从int或float到double,能保留精确数值
从double到float,可能溢出为正无穷或负无穷;可能被舍入
从float或者double到int,值将向0舍入,可能会溢出。
问题:
在这一章中,我们看了这么多种因为没有分析原始定义或者概念而导致的溢出现象,其中不少造成了灾难性后果。那么,对于溢出这种现象,我们是究竟完全不希望其发生呢?还是反过来在某些场合能够将其作为一种功能?亦或是,因为其不可控的特性,我们在实际使用中要尽可能避免其发生,不要尝试使用这种功能?