0.PTA得分截图

1.本周学习总结
1.1 总结线性表内容
1.线性表定义
线性表是具有相同特性的数据元素的一个有序序列。
2.顺序表
(1)结构体定义
#define MAXSIZE 50//最大长度
typedef int ElemType;
typedef struct
{
ElemType *elem;//指向数据元素的基地址
int length; //线性表当前长度
} SqList;
或者
#define MAXSIZE 50//最大长度
typedef int ElemType;
typedef struct
{
ElemType data[MaxSize];//存放顺序表中的元素
int length; //顺序表的长度
} SqList;
建议:typedef SqList *List;
(2)顺序表的基本操作
1.初始化顺序表
typedef int ElemType;
typedef struct
{
ElemType data[MaxSize];//存放顺序表中的元素
int length; //顺序表的长度
} List;
typedef List *SqList;
void CreateList(SqList &L,int n)
{
int i;
L=new List;
L->length=n;
for(i=0;i<n;i++)
{
cin>>L->data[i];
}
}
2.销毁线性表DestroyList(L)
结果是释放线性表L占用的内存空间。
void DestroyList(SqList *&L)
{
free(L);
}
3.输出线性表DispList(L)
void DispList(List L)
{ int i;
if (ListEmpty(L)) return;
for (i=0;i<L->length;i++)
cout<<L->data[i]<<" ";
}
4.获取L中第i个元素
返回L中第i个元素的值,存放在e中。1≤i≤ListLength(L)
bool GetElem(List L,int i,ElemType &e){
if (i<1 || i>L->length)
return false;
e=L->data[i-1];
return true;
}
5.按元素值查找
int LocateElem(List L, ElemType e)
{
for(int i=0; i<L->length;i++)
if(L->data[i]==e)
return i+1; //返回元素的逻辑位序
return 0;
}
6.插入元素
插入做法:
(1).找插入位置
(2).数组元素a[i]--a[n]后移一个位置
(3).a[i]插入数,表长度增1
代码:
bool ListInsert(List &L,int i,ElemType e)
{ int j;
if (i<1 || i>L->length+1)
return false; //参数错误时返回false
i--; //将顺序表逻辑序号转化为物理序号
for (j=L->length;j>i;j--) //将data[i..n]元素后移一个位置
L->data[j]=L->data[j-1];
L->data[i]=e; //插入元素e
L->length++; //顺序表长度增1
return true; //成功插入返回true
}
7.删除元素
bool ListDelete(List &L,int i,ElemType &e)
{
if (i<1 || i>L->length) //删除位置不合法
return false;
i--; //将顺序表逻辑序号转化为物理序号
e=L->data[i];
for (int j=i;j<L->length-1;j++)
L->data[j]=L->data[j+1];
L->length--; //顺序表长度减1
return true;
}
(3)顺序存储结构的优缺点:
优点
逻辑相邻,物理相邻
无须为表示表中元素之间的顺序关系增加额外的存储空间
可随机存取任一元素
存储空间使用紧凑
缺点
插入、删除操作需要移动大量的元素(除操作在表尾的位置进行外)
预先分配空间需按最大空间分配,利用不充分
表容量难以扩充
3.链表
1.链表结构和定义
结构:
节点 = 数据元素 + 指针
1.数据元素:存放数据
2.指针:存放该节点下一个元素的存储位置
定义:
这样的链接表可以存放线性表,称之为链表。
2.线性表基本运算在单链表实现
1.初始化线性表
typedef struct LNode{
ElemType data; //数据域
struct LNode *next; //指针域
}LNode,*LinkList;
Status InitList_L(LinkList &L){
L=new LNode;
L->next=NULL;
return OK;
}
2.建立单链表
头插法:
新增节点从链表头部插入
代码:
void CreateListF(LinkList &L,ElemType a[],int n)
{
int i;
L=new LNode;
L->next=NULL;
LinkList nodePtr;
for(i=0;i<n;i++)
{
nodePtr=new LNode;
nodePtr->data=a[i];
nodePtr->next=L->next;
L->next= nodePtr;
}
}
尾插法:
新增节点从链表尾部插入
代码:
void CreateListR(LinkList &L,ElemType a[],int n)
{
int i;
LinkList nodePtr,tailPtr;
L=new LNode;
L->next=NULL;
tailPtr=L;//尾指针
for(i=0;i<n;i++)
{
nodePtr=new LNode;
nodePtr->data=a[i];
rearPtr->next=s;//尾部插入新结点
rearPtr=s;
}
nodePtr->next=NULL;
}
3.销毁线性表
void DestroyList(LinkList &L)
{
LinkList p;
while(L)
{
p=L;
L=L->next;
delete p;
}
}
4.输出线性表DispList(L)
void DispList(LinkList L)//输出链表
{
LNode* p;
p = L->next;
if (p == NULL)
{
cout << "空链表!";
return;
}
while (p->next)
{
cout << p->data << " ";
p = p->next;
}
cout << p->data;
}
5.查找数据元素
bool GetElem(LinkList L,int i,ElemType &e)
{ int j=0;
LinkList p=L; //p指向头节点,j置为0(即头节点的序号为0)
while (j<i && p!=NULL) //找第i个节点
{ j++;
p=p->next;
}
if (p==NULL) //不存在第i个数据节点,返回false
return false;
else //存在第i个数据节点,返回true
{ e=p->data;
return true;
}
}
6.插入数据元素
在L中第i个元素之前插入数据元素e
bool ListInsert(LinkList &L,int i,ElemType e)
{
int j=0;
LinkList p=L,s;
while(p&&j<i-1)
{
j++;p=p->next;
}
if(p==NULL) return false; //未找到第i-1个结点
s=new LNode;
s->data=e;
s->next=p->next; //插入p后面
p->next=s;
return true;
}
7.删除数据元素
在单链表中删除第 i 个结点的基本操作为:找到线性表中第i-1个结点,修改其指向后继的指针。
bool ListDelete_L(LinkList &L,int i,ElemType &e)
{
int j=0;
LinkList p=L,s,q;
while(p&&j<i-1)
{
p=p->next;j++;
}
if(p==NULL) return false;
q=p->next; //第i个位置
if(q==NULL) return false;
e=q->data;
p->next=q->next;//改变指针关系,删除
delete q;
return true;
}
3.链表中应注意
(1).遍历链表过程中务必考虑指针是否为空,尤其p->next或p->data前务必考虑p是否为空
(2).链表变化,经常要重构。重构做法:
p=L->next;L->next=NULL;
(3).链表做删除时候,务必考虑链表已经空的情况
(4).链表做插入时候,注意要知道插入点的前驱指针在哪里,可以通过pre->next来获取。
(5).要保留指针后继,可设计nextptr=p->next,中间p变化,再p=nextptr。
(6).链表设计,务必画图,了解指针目前状态。
4.有序表
1.定义
所谓有序表,是指这样的线性表,其中所有元素以递增或递减方式有序排列。
2.有序顺序表的插入
void InsertSq(SqList &L,int x)
{
for(int j = L->length; j > 0; j--)
{
if (x >= L->data[j-1]) //找
{
L->data[j] = x;
break;
}
L->data[j] = L->data[j-1];//移动,边移边找
L->data[j-1] = x;//保证第一个数据插入
}
L->length++;
}
3.有序单链表的插入
void ListInsert(LinkNode &L,ElemType e)
{ LinkNode pre=L,p;
while (pre->next!=NULL && pre->next->data<e)
pre=pre->next; //查找插入结点的前驱结点*pre
p=new LinkNode;
p->data=e; //创建存放e的数据结点*p
p->next=pre->next; //在*pre结点之后插入*p结点
pre->next=p;
}
4.两个有序表的合并
void MergeList(LinkList& L1, LinkList L2)//合并链表
{
LinkList ptr1, ptr2, tailptr;
ptr1 = L1->next;
L1->next = NULL;
ptr2 = L2->next;
tailptr = L1;
while (ptr1 && ptr2)
{
if (ptr1->data < ptr2->data)
{
tailptr->next = ptr1;
tailptr = ptr1;
ptr1 = ptr1->next;
}
else if (ptr1->data > ptr2->data)
{
tailptr->next = ptr2;
tailptr = ptr2;
ptr2 = ptr2->next;
}
else
{
tailptr->next = ptr2;
tailptr = ptr2;
ptr2 = ptr2->next;
ptr1 = ptr1->next;
}
}
if (ptr1 != NULL)
tailptr->next = ptr1;
if (ptr2 != NULL)
tailptr->next = ptr2;
}
5.双链表
1.双链表的建立
头插法:
void CreateListF(DLinkNode *&L,ElemType a[],int n)
{ DLinkNode *s; int i;
L=(DLinkNode *)malloc(sizeof(DLinkNode)); //创建头结点
L->prior=L->next=NULL; //前后指针域置为NULL
for (i=0;i<n;i++) //循环建立数据结点
{ s=(DLinkNode *)malloc(sizeof(DLinkNode));
s->data=a[i]; //创建数据结点*s
s->next=L->next; //将*s插入到头结点之后
if (L->next!=NULL) //若L存在数据结点,修改前驱指针
L->next->prior=s;
L->next=s;
s->prior=L;
}
}
尾插法:
void CreateListR(DLinkNode *&L,ElemType a[],int n)
{ DLinkNode *s,*r;
int i;
L=(DLinkNode *)malloc(sizeof(DLinkNode)); //创建头结点
L->prior=L->next=NULL; //前后指针域置为NULL
r=L; //r始终指向尾结点,开始时指向头结点
for (i=0;i<n;i++) //循环建立数据结点
{ s=(DLinkNode *)malloc(sizeof(DLinkNode));
s->data=a[i]; //创建数据结点*s
r->next=s;
s->prior=r; //将*s插入*r之后
r=s; //r指向尾结点
}
r->next=NULL; //尾结点next域置为NULL
}
2.双链表中结点的插入和删除
在p结点之后插入结点s
操作语句:
s->next = p->next
p->next->prior = s
s->prior = p
p->next = s
删除*p结点之后的一个结点
操作语句:
p->next->next->prior = p
p->next = p->next->next
6.循环链表
循环链表是另一种形式的链式存储结构形式。
循环单链表:将表中尾结点的指针域改为指向表头结点,整个链表形成一个环。由此从表中任一结点出发均可找到链表中其他结点。
与单链表区别:
1.从循环链表中的任何一个结点的位置都可以找到其他所有结点,而单链表做不到;
2.循环链表中没有明显的尾端
1.2.谈谈你对线性表的认识及学习体会。
优点:
1.节省存储空间
2.存取表中任一位置的元素时方便快捷
3.用链表表示线性表不受空间限制,在节点的插入、删除方便,不用大量移动数据;
缺点:
1.当长度变化大时,难以确定存储空间的容量
2.顺序存储结构会造成存储空间的“碎片”。
2.顺序存储结构时,插入和删除操作需要移动大量的元素。
学习体会:
顺序存储和链式存储具有不同的优缺点,用线性表操作可以更加方便。
2.PTA实验作业
2.1
------------恢复内容开始------------
0.PTA得分截图
1.本周学习总结
1.1 总结线性表内容
1.线性表定义
线性表是具有相同特性的数据元素的一个有序序列。
2.顺序表
(1)结构体定义
#define MAXSIZE 50//最大长度
typedef int ElemType;
typedef struct
{
ElemType *elem;//指向数据元素的基地址
int length; //线性表当前长度
} SqList;
或者
#define MAXSIZE 50//最大长度
typedef int ElemType;
typedef struct
{
ElemType data[MaxSize];//存放顺序表中的元素
int length; //顺序表的长度
} SqList;
建议:typedef SqList *List;
(2)顺序表的基本操作
1.初始化顺序表
typedef int ElemType;
typedef struct
{
ElemType data[MaxSize];//存放顺序表中的元素
int length; //顺序表的长度
} List;
typedef List *SqList;
void CreateList(SqList &L,int n)
{
int i;
L=new List;
L->length=n;
for(i=0;i<n;i++)
{
cin>>L->data[i];
}
}
2.销毁线性表DestroyList(L)
结果是释放线性表L占用的内存空间。
void DestroyList(SqList *&L)
{
free(L);
}
3.输出线性表DispList(L)
void DispList(List L)
{ int i;
if (ListEmpty(L)) return;
for (i=0;i<L->length;i++)
cout<<L->data[i]<<" ";
}
4.获取L中第i个元素
返回L中第i个元素的值,存放在e中。1≤i≤ListLength(L)
bool GetElem(List L,int i,ElemType &e){
if (i<1 || i>L->length)
return false;
e=L->data[i-1];
return true;
}
5.按元素值查找
int LocateElem(List L, ElemType e)
{
for(int i=0; i<L->length;i++)
if(L->data[i]==e)
return i+1; //返回元素的逻辑位序
return 0;
}
6.插入元素
插入做法:
(1).找插入位置
(2).数组元素a[i]--a[n]后移一个位置
(3).a[i]插入数,表长度增1
代码:
bool ListInsert(List &L,int i,ElemType e)
{ int j;
if (i<1 || i>L->length+1)
return false; //参数错误时返回false
i--; //将顺序表逻辑序号转化为物理序号
for (j=L->length;j>i;j--) //将data[i..n]元素后移一个位置
L->data[j]=L->data[j-1];
L->data[i]=e; //插入元素e
L->length++; //顺序表长度增1
return true; //成功插入返回true
}
7.删除元素
bool ListDelete(List &L,int i,ElemType &e)
{
if (i<1 || i>L->length) //删除位置不合法
return false;
i--; //将顺序表逻辑序号转化为物理序号
e=L->data[i];
for (int j=i;j<L->length-1;j++)
L->data[j]=L->data[j+1];
L->length--; //顺序表长度减1
return true;
}
(3)顺序存储结构的优缺点:
优点
逻辑相邻,物理相邻
无须为表示表中元素之间的顺序关系增加额外的存储空间
可随机存取任一元素
存储空间使用紧凑
缺点
插入、删除操作需要移动大量的元素(除操作在表尾的位置进行外)
预先分配空间需按最大空间分配,利用不充分
表容量难以扩充
3.链表
1.链表结构和定义
结构:
节点 = 数据元素 + 指针
1.数据元素:存放数据
2.指针:存放该节点下一个元素的存储位置
定义:
这样的链接表可以存放线性表,称之为链表。
2.线性表基本运算在单链表实现
1.初始化线性表
typedef struct LNode{
ElemType data; //数据域
struct LNode *next; //指针域
}LNode,*LinkList;
Status InitList_L(LinkList &L){
L=new LNode;
L->next=NULL;
return OK;
}
2.建立单链表
头插法:
新增节点从链表头部插入
代码:
void CreateListF(LinkList &L,ElemType a[],int n)
{
int i;
L=new LNode;
L->next=NULL;
LinkList nodePtr;
for(i=0;i<n;i++)
{
nodePtr=new LNode;
nodePtr->data=a[i];
nodePtr->next=L->next;
L->next= nodePtr;
}
}
尾插法:
新增节点从链表尾部插入
代码:
void CreateListR(LinkList &L,ElemType a[],int n)
{
int i;
LinkList nodePtr,tailPtr;
L=new LNode;
L->next=NULL;
tailPtr=L;//尾指针
for(i=0;i<n;i++)
{
nodePtr=new LNode;
nodePtr->data=a[i];
rearPtr->next=s;//尾部插入新结点
rearPtr=s;
}
nodePtr->next=NULL;
}
3.销毁线性表
void DestroyList(LinkList &L)
{
LinkList p;
while(L)
{
p=L;
L=L->next;
delete p;
}
}
4.输出线性表DispList(L)
void DispList(LinkList L)//输出链表
{
LNode* p;
p = L->next;
if (p == NULL)
{
cout << "空链表!";
return;
}
while (p->next)
{
cout << p->data << " ";
p = p->next;
}
cout << p->data;
}
5.查找数据元素
bool GetElem(LinkList L,int i,ElemType &e)
{ int j=0;
LinkList p=L; //p指向头节点,j置为0(即头节点的序号为0)
while (j<i && p!=NULL) //找第i个节点
{ j++;
p=p->next;
}
if (p==NULL) //不存在第i个数据节点,返回false
return false;
else //存在第i个数据节点,返回true
{ e=p->data;
return true;
}
}
6.插入数据元素
在L中第i个元素之前插入数据元素e
bool ListInsert(LinkList &L,int i,ElemType e)
{
int j=0;
LinkList p=L,s;
while(p&&j<i-1)
{
j++;p=p->next;
}
if(p==NULL) return false; //未找到第i-1个结点
s=new LNode;
s->data=e;
s->next=p->next; //插入p后面
p->next=s;
return true;
}
7.删除数据元素
在单链表中删除第 i 个结点的基本操作为:找到线性表中第i-1个结点,修改其指向后继的指针。
bool ListDelete_L(LinkList &L,int i,ElemType &e)
{
int j=0;
LinkList p=L,s,q;
while(p&&j<i-1)
{
p=p->next;j++;
}
if(p==NULL) return false;
q=p->next; //第i个位置
if(q==NULL) return false;
e=q->data;
p->next=q->next;//改变指针关系,删除
delete q;
return true;
}
3.链表中应注意
(1).遍历链表过程中务必考虑指针是否为空,尤其p->next或p->data前务必考虑p是否为空
(2).链表变化,经常要重构。重构做法:
p=L->next;L->next=NULL;
(3).链表做删除时候,务必考虑链表已经空的情况
(4).链表做插入时候,注意要知道插入点的前驱指针在哪里,可以通过pre->next来获取。
(5).要保留指针后继,可设计nextptr=p->next,中间p变化,再p=nextptr。
(6).链表设计,务必画图,了解指针目前状态。
4.有序表
1.定义
所谓有序表,是指这样的线性表,其中所有元素以递增或递减方式有序排列。
2.有序顺序表的插入
void InsertSq(SqList &L,int x)
{
for(int j = L->length; j > 0; j--)
{
if (x >= L->data[j-1]) //找
{
L->data[j] = x;
break;
}
L->data[j] = L->data[j-1];//移动,边移边找
L->data[j-1] = x;//保证第一个数据插入
}
L->length++;
}
3.有序单链表的插入
void ListInsert(LinkNode &L,ElemType e)
{ LinkNode pre=L,p;
while (pre->next!=NULL && pre->next->data<e)
pre=pre->next; //查找插入结点的前驱结点*pre
p=new LinkNode;
p->data=e; //创建存放e的数据结点*p
p->next=pre->next; //在*pre结点之后插入*p结点
pre->next=p;
}
4.两个有序表的合并
void MergeList(LinkList& L1, LinkList L2)//合并链表
{
LinkList ptr1, ptr2, tailptr;
ptr1 = L1->next;
L1->next = NULL;
ptr2 = L2->next;
tailptr = L1;
while (ptr1 && ptr2)
{
if (ptr1->data < ptr2->data)
{
tailptr->next = ptr1;
tailptr = ptr1;
ptr1 = ptr1->next;
}
else if (ptr1->data > ptr2->data)
{
tailptr->next = ptr2;
tailptr = ptr2;
ptr2 = ptr2->next;
}
else
{
tailptr->next = ptr2;
tailptr = ptr2;
ptr2 = ptr2->next;
ptr1 = ptr1->next;
}
}
if (ptr1 != NULL)
tailptr->next = ptr1;
if (ptr2 != NULL)
tailptr->next = ptr2;
}
5.双链表
1.双链表的建立
头插法:
void CreateListF(DLinkNode *&L,ElemType a[],int n)
{ DLinkNode *s; int i;
L=(DLinkNode *)malloc(sizeof(DLinkNode)); //创建头结点
L->prior=L->next=NULL; //前后指针域置为NULL
for (i=0;i<n;i++) //循环建立数据结点
{ s=(DLinkNode *)malloc(sizeof(DLinkNode));
s->data=a[i]; //创建数据结点*s
s->next=L->next; //将*s插入到头结点之后
if (L->next!=NULL) //若L存在数据结点,修改前驱指针
L->next->prior=s;
L->next=s;
s->prior=L;
}
}
尾插法:
void CreateListR(DLinkNode *&L,ElemType a[],int n)
{ DLinkNode *s,*r;
int i;
L=(DLinkNode *)malloc(sizeof(DLinkNode)); //创建头结点
L->prior=L->next=NULL; //前后指针域置为NULL
r=L; //r始终指向尾结点,开始时指向头结点
for (i=0;i<n;i++) //循环建立数据结点
{ s=(DLinkNode *)malloc(sizeof(DLinkNode));
s->data=a[i]; //创建数据结点*s
r->next=s;
s->prior=r; //将*s插入*r之后
r=s; //r指向尾结点
}
r->next=NULL; //尾结点next域置为NULL
}
2.双链表中结点的插入和删除
在p结点之后插入结点s
操作语句:
s->next = p->next
p->next->prior = s
s->prior = p
p->next = s
删除*p结点之后的一个结点
操作语句:
p->next->next->prior = p
p->next = p->next->next
6.循环链表
循环链表是另一种形式的链式存储结构形式。
循环单链表:将表中尾结点的指针域改为指向表头结点,整个链表形成一个环。由此从表中任一结点出发均可找到链表中其他结点。
与单链表区别:
1.从循环链表中的任何一个结点的位置都可以找到其他所有结点,而单链表做不到;
2.循环链表中没有明显的尾端
1.2.谈谈你对线性表的认识及学习体会。
优点:
1.节省存储空间
2.存取表中任一位置的元素时方便快捷
3.用链表表示线性表不受空间限制,在节点的插入、删除方便,不用大量移动数据;
缺点:
1.当长度变化大时,难以确定存储空间的容量
2.顺序存储结构会造成存储空间的“碎片”。
2.顺序存储结构时,插入和删除操作需要移动大量的元素。
学习体会:
顺序存储和链式存储具有不同的优缺点,用线性表操作可以更加方便。
2.PTA实验作业
2.1区间删除数据
2.1.1代码截图
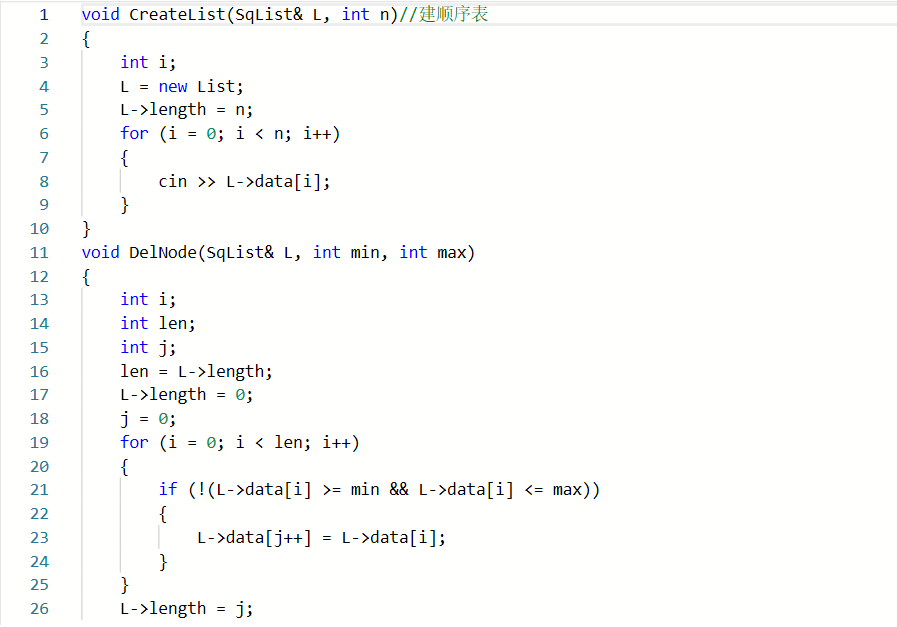

2.1.2本题PTA提交列表说明。

部分正确:输出的时候尾部多了一个空格,自己逐步调试发现问题
部分正确:线性表为空的时候输出错误,请教同学发现是判断条件错了
2.2有序链表合并
2.2.1代码截图
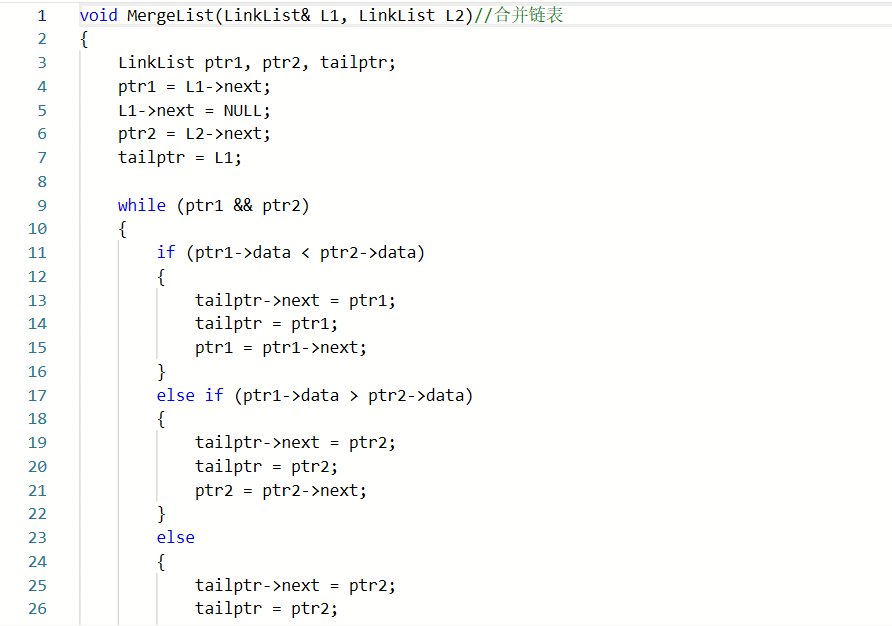
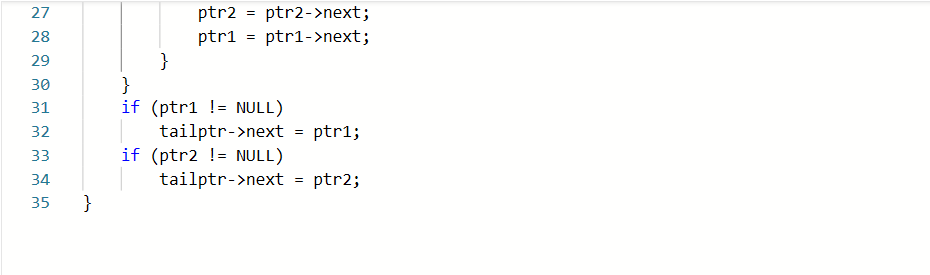
2.2.2本题PTA提交列表说明。

部分正确:没有考虑链表没有比较完的情况
多种错误:添加链表没有比较完时代码错误,后来回顾了之前的讲解才改正
2.3链表倒数第m个数
2.3.1代码截图
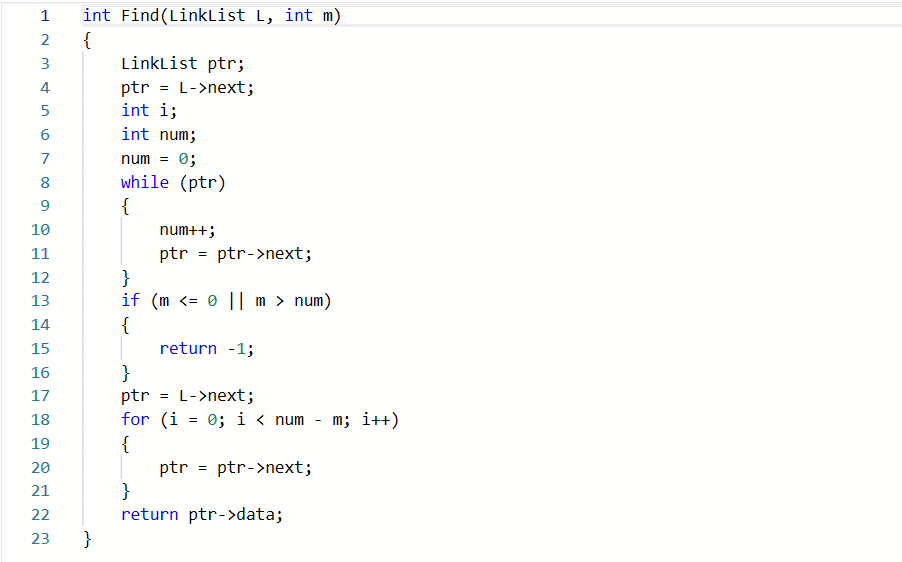
2.3.2本题PTA提交列表说明。
编译错误:有两条语句写错了
部分正确:倒数最后一个数的地方错误,后来请教了同学才改正。
3.阅读代码
3.1反转链表
题目:反转从位置 m 到 n 的链表。请使用一趟扫描完成反转。
说明:
1 ≤ m ≤ n ≤ 链表长度。
示例:
输入: 1->2->3->4->5->NULL, m = 2, n = 4
输出: 1->4->3->2->5->NULL
代码:
/**
* Definition for singly-linked list.
* struct ListNode {
* int val;
* ListNode *next;
* ListNode(int x) : val(x), next(NULL) {}
* };
*/
class Solution {
public:
ListNode* reverseBetween(ListNode* head, int m, int n) {
ListNode* dummy=new ListNode(-1);
ListNode* pre=dummy;
dummy->next=head;
for(int i=0;i<m-1;i++)
pre=pre->next;
ListNode* cur=pre->next;
for(int i=m;i<n;i++){
ListNode* t=cur->next;
cur->next=t->next;
t->next=pre->next;
pre->next=t;
}
return dummy->next;
}
};
3.1.1该题的设计思路
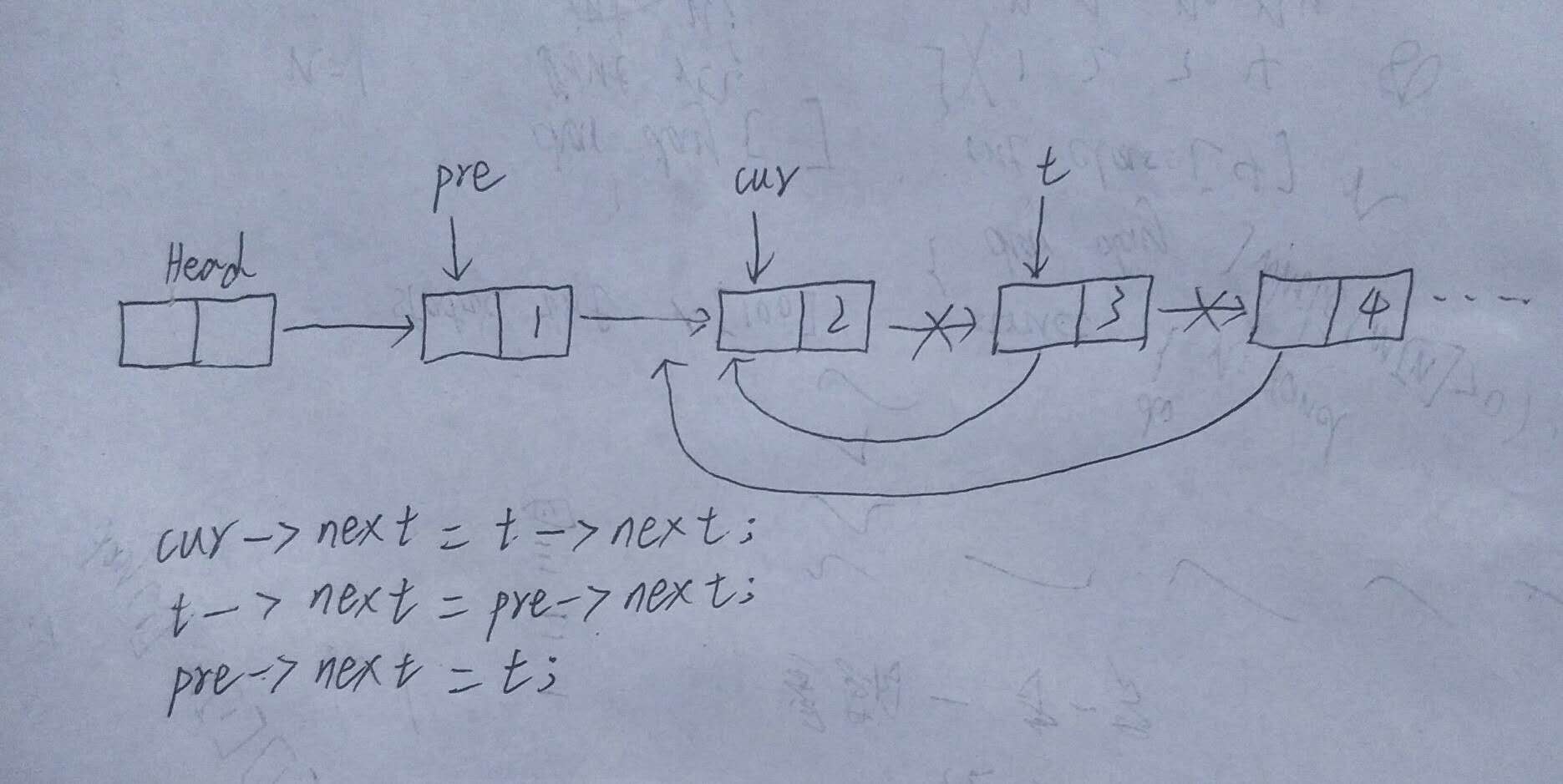
时间复杂度:O(n)
空间复杂度:O(1)
3.1.2该题的伪代码
for i to m-1
结点1pre=结点1的next;
结点2cur=结点1的next;
for i=m to n
临时结点t=结点2的next;
cur->next=t->next;
t->next=pre->next;
pre->next=t;
end for
3.1.3运行结果

3.1.4分析该题目解题优势及难点。
优势:思路简洁清晰,用了所熟悉的头插法,不容易出错,只需遍历一遍。
难点:只能遍历一遍
3.2旋转链表
题目:给定一个链表,旋转链表,将链表每个节点向右移动 k 个位置,其中 k 是非负数。
示例 1:
输入: 1->2->3->4->5->NULL, k = 2
输出: 4->5->1->2->3->NULL
解释:
向右旋转 1 步: 5->1->2->3->4->NULL
向右旋转 2 步: 4->5->1->2->3->NULL
代码:
class Solution {
public ListNode rotateRight(ListNode head, int k) {
// base cases
if (head == null) return null;
if (head.next == null) return head;
// close the linked list into the ring
ListNode old_tail = head;
int n;
for(n = 1; old_tail.next != null; n++)
old_tail = old_tail.next;
old_tail.next = head;
// find new tail : (n - k % n - 1)th node
// and new head : (n - k % n)th node
ListNode new_tail = head;
for (int i = 0; i < n - k % n - 1; i++)
new_tail = new_tail.next;
ListNode new_head = new_tail.next;
// break the ring
new_tail.next = null;
return new_head;
}
}
3.2.1该题的设计思路
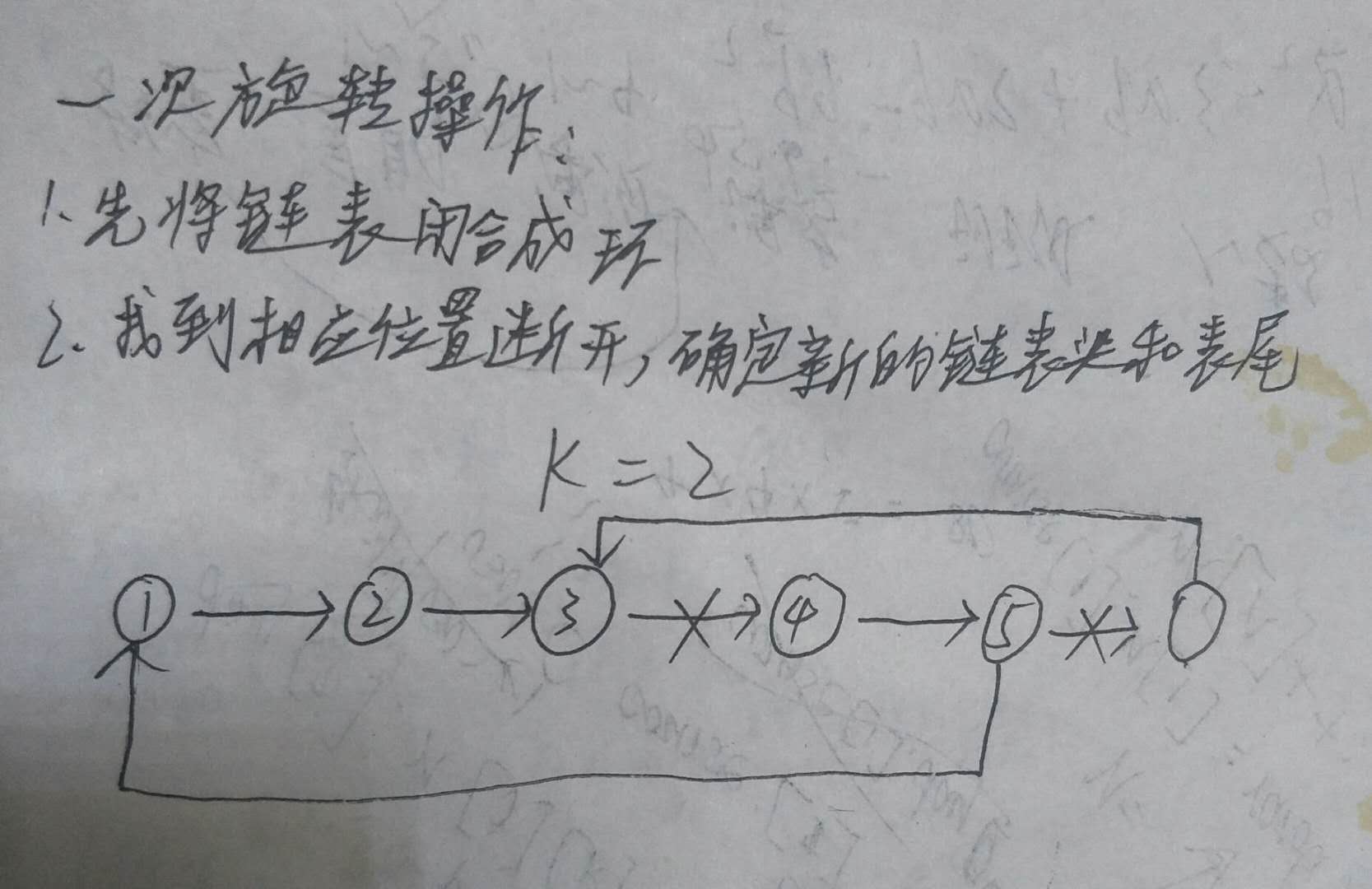
时间复杂度:O(n)
空间复杂度:O(1)
3.2.2该题的伪代码
for n to old-tail.next不为空
旧尾结点=旧尾结点的next;
旧尾结点的next=头结点;
end for
for i to n-k%n-1
新尾结点=新尾结点的next;
新头结点=新尾结点的next;
新尾结点的next=null;
end for
return 新头结点
3.2.3运行结果

3.2.4分析该题目解题优势及难点。
优势:闭合成循环链表,方便寻找新表头
难点:新尾部的结点位置不容易找准