(奇奇怪怪的dp)
题目大意
设有N*N的方格图(N<=20,我们将其中的某些方格中填入正整数,而其他的方格中则放入数字0。如下图所示(见样例):
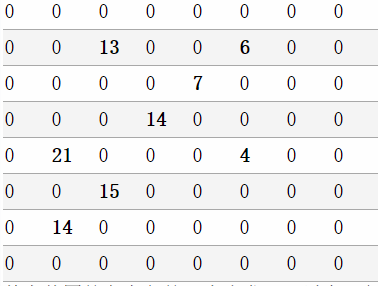
某人从图的左上角的A(1,1) 点出发,可以向下行走,也可以向右走,直到到达右下角的B(n,n)点。在走过的路上(包括起点在内),他可以取走方格中的数(取走后的方格中将变为数字0)。此人从A点到B 点共走两次,试找出2条这样的路径,使得取得的数之和为最大。
输入格式
输入的第一行为一个整数N(表示N*N的方格图)
接下来的每行有三个整数,前两个表示位置,第三个数为该位置上所放的数。一行单独的0表示输入结束。
输出格式
只需输出一个整数,表示2条路径上取得的最大的和
样例
样例输入
8
2 3 13
2 6 6
3 5 7
4 4 14
5 2 21
5 6 4
6 3 15
7 2 14
0 0 0
样例输出
67
算法分析
- 这样的题裸眼就能看出来是dp了吧…………
- 选出两条道路 使得两条道路的和最大 怎么转移呢? 先来想想我们平时的dp题 一般这样的题都是枚举坐标 然后这个坐标可以由他的上边或者左边转移过来 挑一个较大值 然后再加上当前位置的权值(如果有的话)
- 那这个题我们就让dp的主人公有一个分身 (就是开四维呗)他俩一起走 如果两个人到了相同的位置(而且当前位置有权值)就加上这个位置的权值 如果两个人到了不同的位置(而且有权值) 就分别加上两个人所在位置的权值
代码展示
#include<bits/stdc++.h>
using namespace std;
const int maxn = 30;
int f[30][30][30][30],a[maxn][maxn];
int x,y,c;
int main(){
int n;
scanf("%d",&n);
while(1){//输入
scanf("%d%d%d",&x,&y,&c);
if(x == y && y == c && x==c && x==0)break;
a[x][y] = c;//为节点附权值
}
f[1][1][1][1] = a[1][1];//初始化
//枚举俩个人分别的位置
for(int i = 1;i <= n;++i){//枚举第一个人的横坐标
for(int j = 1;j <= n;++j){//枚举第一个人的纵坐标
for(int k = 1;k <= n;++k){//枚举第二个人的横坐标
for(int l = 1;l <= n;++l){//枚举第二个人的纵坐标
if(i == k && j == l)f[i][j][k][l] = max(f[i-1][j][k-1][l],max(f[i-1][j][k][l-1],max(f[i][j-1][k-1][l],f[i][j-1][k][l-1]))) + a[i][j];//如果两个人到了相同的位置
else f[i][j][k][l] = max(f[i-1][j][k-1][l],max(f[i-1][j][k][l-1],max(f[i][j-1][k-1][l],f[i][j-1][k][l-1]))) + a[i][j] + a[k][l];//如果两个人到了不同的位置
}
}
}
}
printf("%d",f[n][n][n][n]);
return 0;
}
写在后面:
-
这个题n的数据范围并不大(只有20),因此开四维的数组还是绰绰有余的 但是如果这个题的数据改大呢?
-
再来想想本体和分身的行路规则 我们可以发现: 本体所走的路程 = 分身所走的路程 = 本体的横坐标 + 本体的纵坐标 - 2= 分身的横坐标 + 分身的纵坐标 - 2(如果起点为(1,1)的话)
-
这样我们就可以第一维枚举已经走过的步数 , 第二维是第一个人的横坐标 第三维是第二个人的横坐标(知道横坐标和步数也就知道纵坐标了吧) 然后同样的方法去dp求解就好了
-
代码请自行写出(
博主不是因为懒所以不加的) -
还有一种可以压到二维(
请自行查找洛谷题解)
谢谢观看
点个关注>?<