实现二叉树
要求:参考教材p375,完成链树LinkedBinaryTree的实现(getRight,contains,toString,preorder,postorder)用JUnit或自己编写驱动类对自己实现的LinkedBinaryTree进行测试,提交测试代码运行截图,要全屏,包含自己的学号信息,课下把代码推送到代码托管平台.
实验思路:getright仿照书上getleft格式即可;contains方法调用find方法,返回值则是boolean类型;preorder和postorder方法则和inorder方法有些类似,都是调用BTnode类并递归;
实验截图: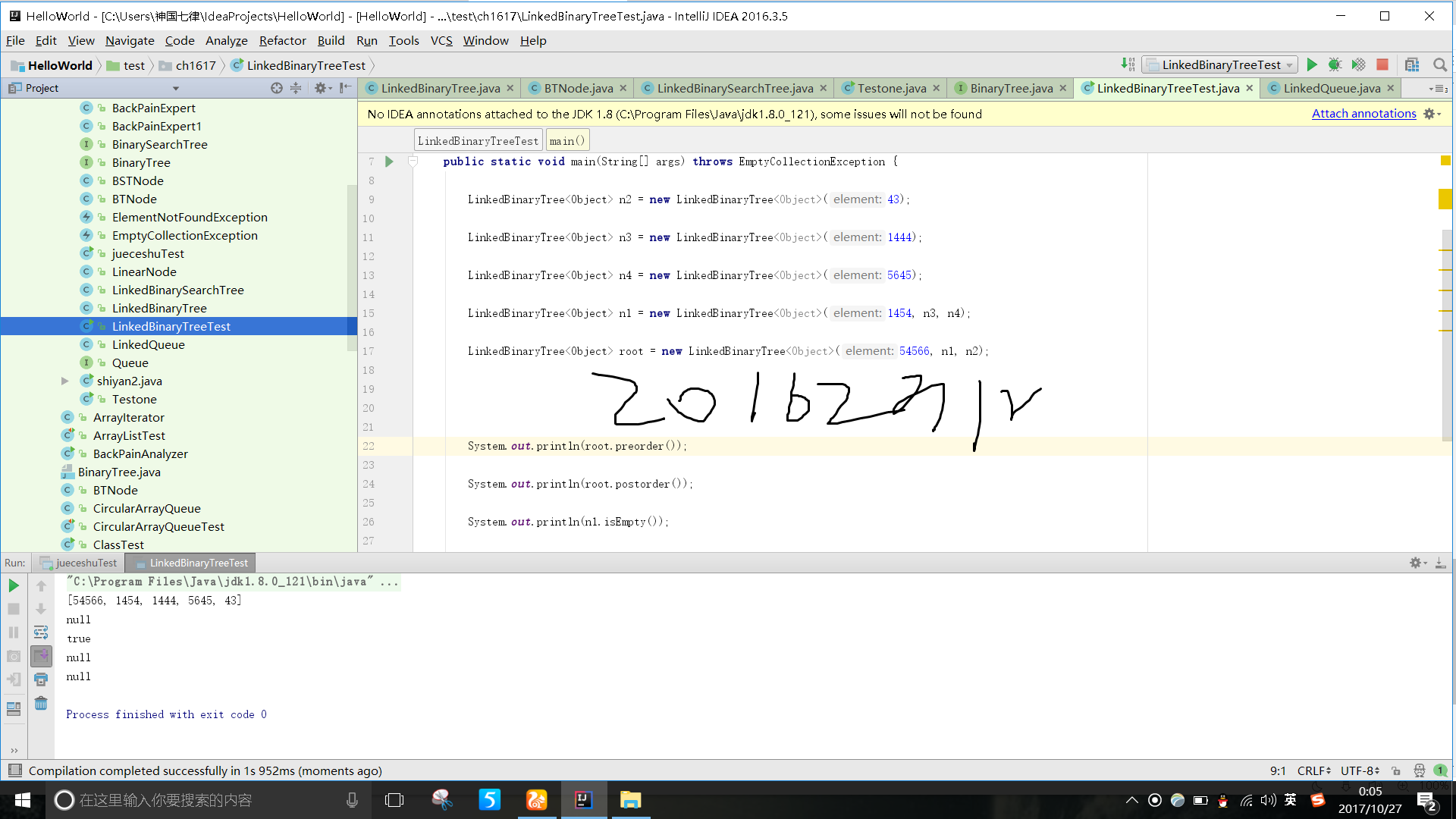
中序先序序列构造二叉树
要求:基于LinkedBinaryTree,实现基于(中序,先序)序列构造唯一一棵二㕚树的功能,比如教材P372,给出HDIBEMJNAFCKGL和ABDHIEJMNCFGKL,构造出附图中的树
用JUnit或自己编写驱动类对自己实现的功能进行测试,提交测试代码运行截图,要全屏,包含自己的学号信息
课下把代码推送到代码托管平台
实验思路:将左子树中的元素的先序表达式放入新的数组
实验截图: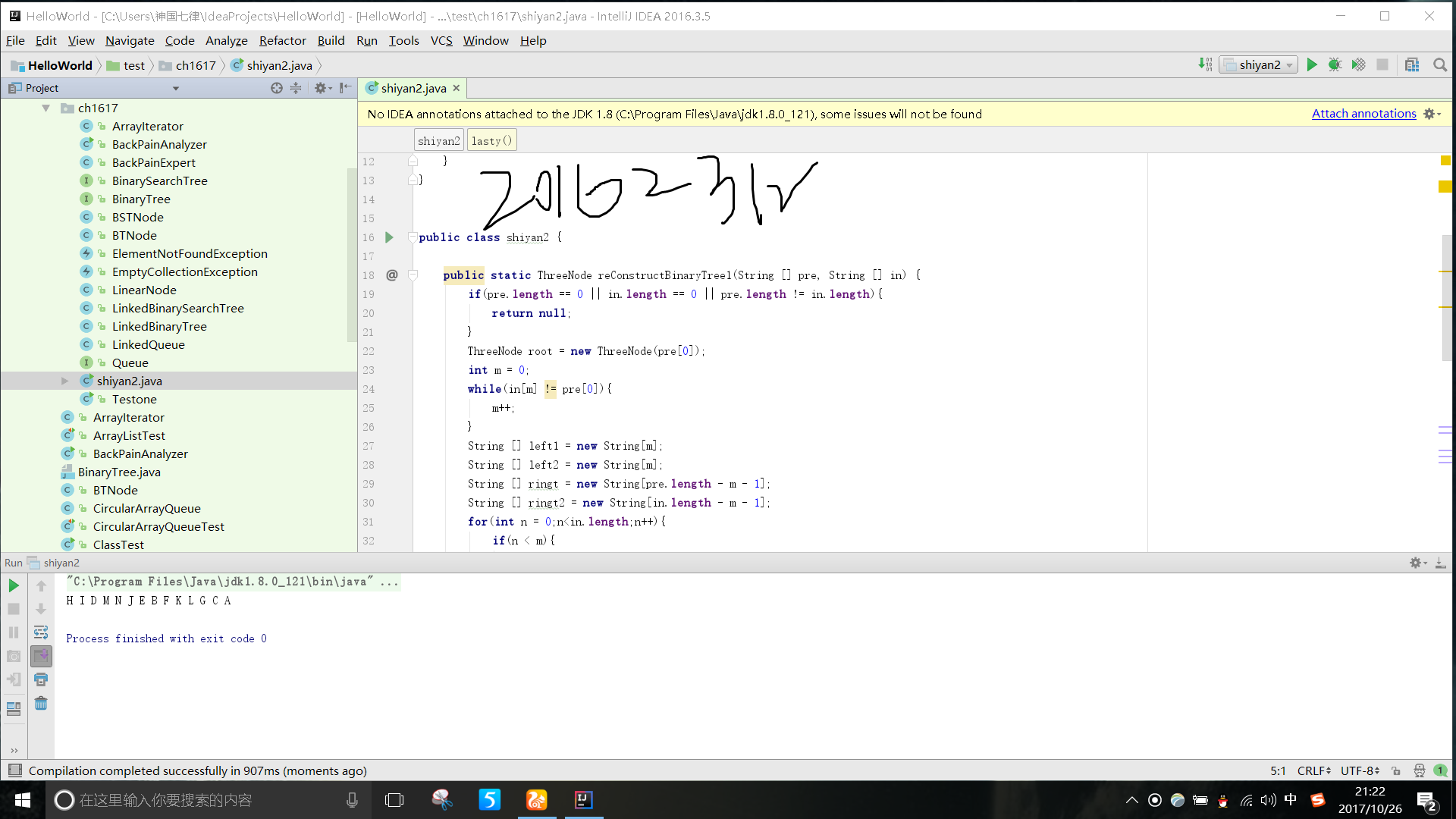
决策树
要求:完成PP16.6,提交测试代码运行截图,要全屏,包含自己的学号信息,课下把代码推送到代码托管平台.
实验思路:主要是改书上的代码,但要对树的构造比较清楚,并且自己设定的内容逻辑要和树的构造相符。
实验截图: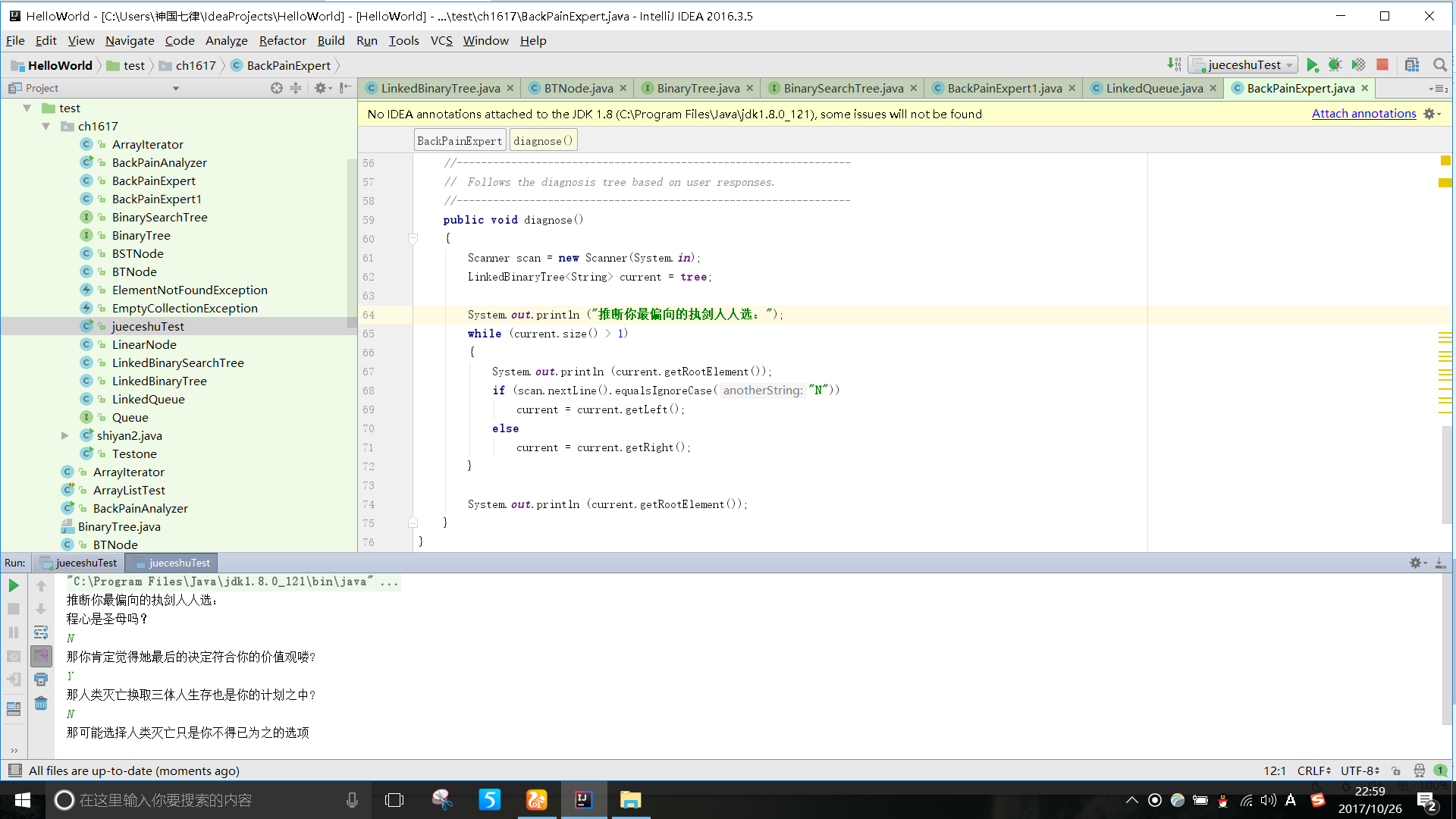
表达式树
要求:完成PP16.8,提交测试代码运行截图,要全屏,包含自己的学号信息,课下把代码推送到代码托管平台
实验思路:没有完成
二叉查找树
要求:完成PP17.1,提交测试代码运行截图,要全屏,包含自己的学号信息,课下把代码推送到代码托管平台.
实验思路:很容易补全findMax(),findMin()方法.
实验截图: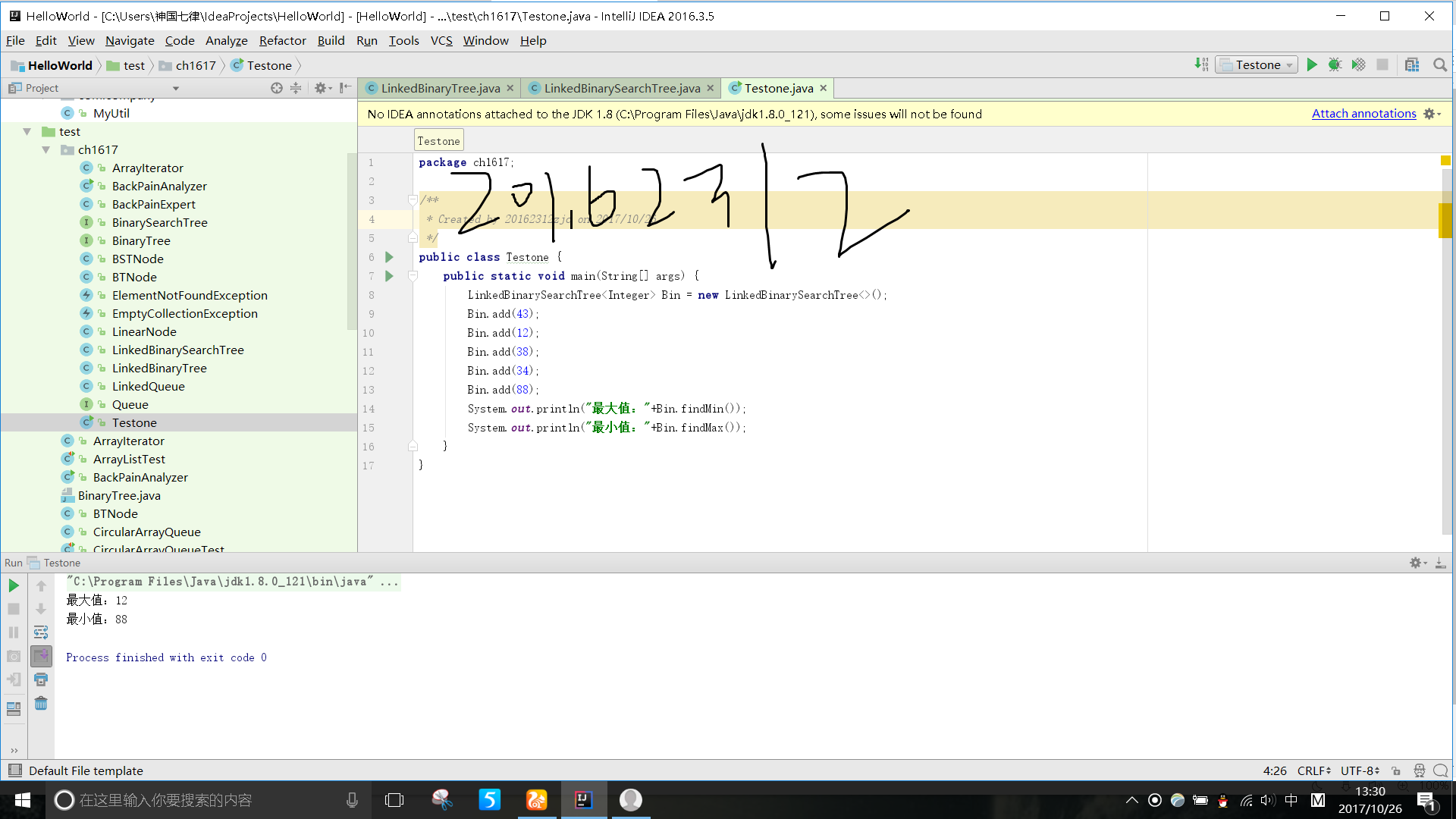
红黑树分析
要求:参考http://www.cnblogs.com/rocedu/p/7483915.html对Java中的红黑树(TreeMap,HashMap)进行源码分析,并在实验报告中体现分析结果
实验思路:分析源代码并上网参考相关资料
什么是红黑树
- 每个节点要么是红色,要么是黑色。
- 根节点必须是黑色
- 红色节点不能连续(也即是,红色节点的孩子和父亲都不能是红色)。
- 对于每个节点,从该点至null(树尾端)的任何路径,都含有相同个数的黑色节点。
左旋及代码实现

//Rotate Left
private void rotateLeft(Entry<K,V> p) {
if (p != null) {
Entry<K,V> r = p.right;
p.right = r.left;
if (r.left != null)
r.left.parent = p;
r.parent = p.parent;
if (p.parent == null)
root = r;
else if (p.parent.left == p)
p.parent.left = r;
else
p.parent.right = r;
r.left = p;
p.parent = r;
}
}
右旋及代码实现
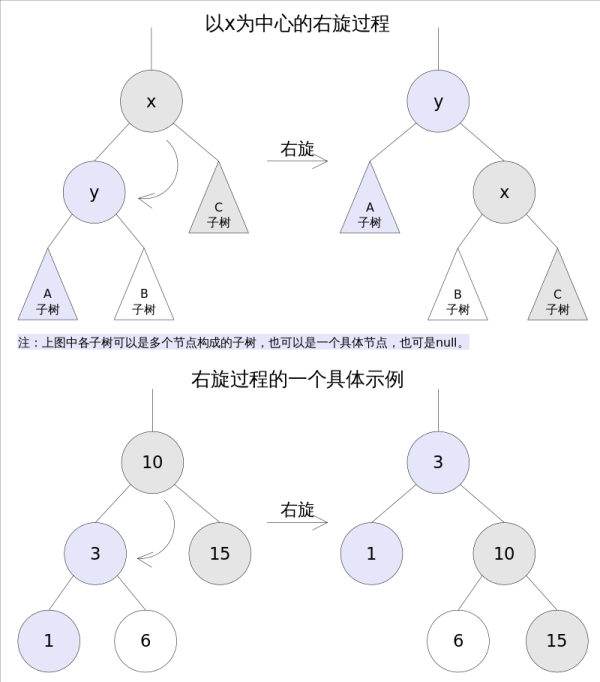
//Rotate Right
private void rotateRight(Entry<K,V> p) {
if (p != null) {
Entry<K,V> l = p.left;
p.left = l.right;
if (l.right != null) l.right.parent = p;
l.parent = p.parent;
if (p.parent == null)
root = l;
else if (p.parent.right == p)
p.parent.right = l;
else p.parent.left = l;
l.right = p;
p.parent = l;
}
}
方法剖析:
- 方法get(Object key)方法根据指定的key值返回对应的value,该方法调用了getEntry(Object key)得到相应的entry,然后返回entry.value。
因此getEntry()是算法的核心。算法思想是根据key的自然顺序(或者比较器顺序)对二叉查找树进行查找,直到找到满足k.compareTo(p.key) == 0的entry。
//getEntry()方法
final Entry<K,V> getEntry(Object key) {
......
if (key == null)//不允许key值为null
throw new NullPointerException();
Comparable<? super K> k = (Comparable<? super K>) key;//使用元素的自然顺序
Entry<K,V> p = root;
while (p != null) {
int cmp = k.compareTo(p.key);
if (cmp < 0)//向左找
p = p.left;
else if (cmp > 0)//向右找
p = p.right;
else
return p;
}
return null;
}
- 方法put(K key, V value)方法是将指定的key, value对添加到map里。该方法首先会对map做一次查找,看是否包含该元组,如果已经包含则直接返回,
查找过程类似于getEntry()方法;如果没有找到则会在红黑树中插入新的entry,如果插入之后破坏了红黑树的约束,还需要进行调整(旋转,改变某些节点的颜色)。
public V put(K key, V value) {
......
int cmp;
Entry<K,V> parent;
if (key == null)
throw new NullPointerException();
Comparable<? super K> k = (Comparable<? super K>) key;//使用元素的自然顺序
do {
parent = t;
cmp = k.compareTo(t.key);
if (cmp < 0) t = t.left;//向左找
else if (cmp > 0) t = t.right;//向右找
else return t.setValue(value);
} while (t != null);
Entry<K,V> e = new Entry<>(key, value, parent);//创建并插入新的entry
if (cmp < 0) parent.left = e;
else parent.right = e;
fixAfterInsertion(e);//调整
size++;
return null;
}
- 方法remove的作用是删除key值对应的entry,该方法首先通过上文中提到的getEntry(Object key)方法找到key值对应的entry,
然后调用deleteEntry(Entry<K,V> entry)删除对应的entry。由于删除操作会改变红黑树的结构,有可能破坏红黑树的约束,因此有可能要进行调整。