上一节讲了时间复杂度和空间复杂度,以及常用的时间复杂度分析方法。这一节更深入的介绍了几种复杂度概念,在不同情况下的复杂度
最好情况时间复杂度(best case time complexity)、最坏情况时间复杂度(worst case time complexity)、平均情况时间复杂度(average case time complexity)、均摊时间复杂度(amortized time complexity)。
平均时间复杂度的全称应该叫加权平均时间复杂度或者期望时间复杂度。
平均复杂度分析方法:找出所有的输入情况及相应的发生概率,然后再计算加权平均值。
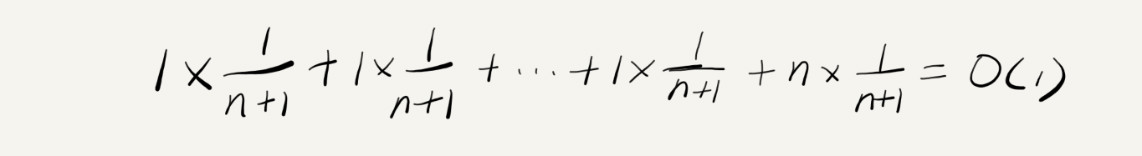
摊还分析(或者叫平摊分析):每一次 O(n) 的插入操作,都会跟着 n-1 次 O(1) 的插入操作,所以把耗时多的那次操作均摊到接下来的 n-1 次耗时少的操作上,均摊下来,这一组连续的操作的均摊时间复杂度就是 O(1)。
通过摊还分析得到的时间复杂度我们起了一个名字,叫均摊时间复杂度。
对一个数据结构进行一组连续操作中,大部分情况下时间复杂度都很低,只有个别情况下时间复杂度比较高,而且这些操作之间存在前后连贯的时序关系,这个时候,我们就可以将这一组操作放在一块儿分析,看是否能将较高时间复杂度那次操作的耗时,平摊到其他那些时间复杂度比较低的操作上。而且,在能够应用均摊时间复杂度分析的场合,一般均摊时间复杂度就等于最好情况时间复杂度。均摊时间复杂度就是一种特殊的平均时间复杂度